Gravité avec axe vers le bas
Définition 
Lorsque l'on utilise un système de coordonnées avec un axe z positif pointant vers le haut, la gravité correspond à un processus d\'accélération dans la direction vers le bas:

ID:(2249, 0)
Gravité avec axe pointant vers le haut
Image 
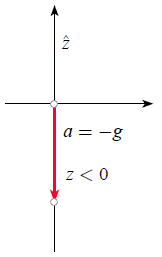
Lorsque l'on utilise un système de coordonnées avec un axe z négatif pointant vers le bas, la gravité correspond à un processus d\'accélération dans la même direction que l\'axe z:
ID:(2250, 0)
Gravitation
Storyboard 
Variables
Calculs
Calculs
Équations
Exemples
Si un corps est d crit dans un syst me de coordonn es o l'axe z pointe \"vers le haut\" (vers le ciel), l\'acc l ration laquelle il est expos est gale l\'acc l ration gravitationnelle, d finie comme n gative :
$a = -g < 0$
Comme l\'acc l ration est constante, la vitesse voluera de mani re lin aire, comme indiqu dans l\' quation suivante :
Par cons quent, dans ce cas, elle peut tre r duite l\' quation suivante :
Lorsque l'on utilise un syst me de coordonn es avec un axe z positif pointant vers le haut, la gravit correspond un processus d\'acc l ration dans la direction vers le bas:
Si un corps est d crit dans un syst me de coordonn es o l'axe z pointe \"vers le bas\" (vers le sol), l\'acc l ration laquelle il est expos est gale l\'acc l ration gravitationnelle, d finie comme positive :
$a = g > 0$
Comme l\'acc l ration est constante, la vitesse voluera de mani re lin aire, comme indiqu dans l\' quation suivante :
Par cons quent, dans ce cas, elle peut tre r duite l\' quation suivante :
Lorsque l'on utilise un syst me de coordonn es avec un axe z n gatif pointant vers le bas, la gravit correspond un processus d\'acc l ration dans la m me direction que l\'axe z:
ID:(1383, 0)
