Torque Generation
Storyboard 
The torque is generated by a force applied at a certain distance from the axis of rotation. Forces on a point on the axis of rotation only lead to translation and do not induce changes in rotation or torque.The shortest distance between the point that attacks the force and the axis is called the arm and this is always perpendicular to the axis. A force parallel to the arm only generates shaft translation so that only the forces perpendicular to the arm generate torque.Finally it is seen that the torque is greater the greater the arm and the greater the force perpendicular to the arm.
ID:(1416, 0)
Force and Torque
Description 
As we have seen, torque plays a role analogous to force in the case of rotation:
$F\longleftrightarrow T$
To establish the equations of motion, we can recall how force was defined in terms of momentum:
$F=\displaystyle\frac{\Delta p}{\Delta t}$
and how torque was defined:
$T=\displaystyle\frac{\Delta L}{\Delta t}$
We can establish a relationship between the two to describe the generation of torque based on force:

Hence, we must first define what the equivalent of Momentum is in the context of rotation.
ID:(325, 0)
Center of mass (CM) concept
Image 
If one considers the distribution of mass in space, it should always be possible to identify a point where the force exerted by the mass on one side is equal to the force generated on the other side:

This concept implies that for any orientation of an object, a point of support can be located, at which the object is in balance. Each of these points corresponds to a vertical line. By repeating this process with different orientations of the object, it eventually becomes evident that the vertical lines intersect at a particular point within the object. This point is referred to as the center of mass (CM). In essence, the center of mass is the unique point within the object where, regardless of its orientation, equilibrium is always achieved.
ID:(323, 0)
Definition of the center of mass (CM)
Image 
One can define the center of mass as the point at which all the vertical lines drawn through points where the system is in equilibrium intersect:
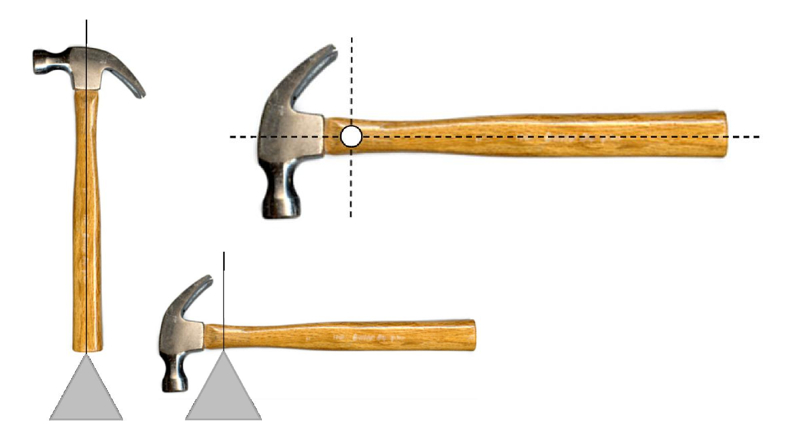
ID:(11603, 0)
Path of a body with translation and rotation
Image 
Any object that both translates and rotates does so in a manner that:
• its translational motion can be described as if all the mass were concentrated at its center of mass,
• its rotation occurs around the center of mass as if it were not undergoing translation.

ID:(11604, 0)
Torque, right hand rule
Image 
The orientation of torque can be determined using the right-hand rule: if you point your fingers in the direction of the radius and rotate in the direction of the force,
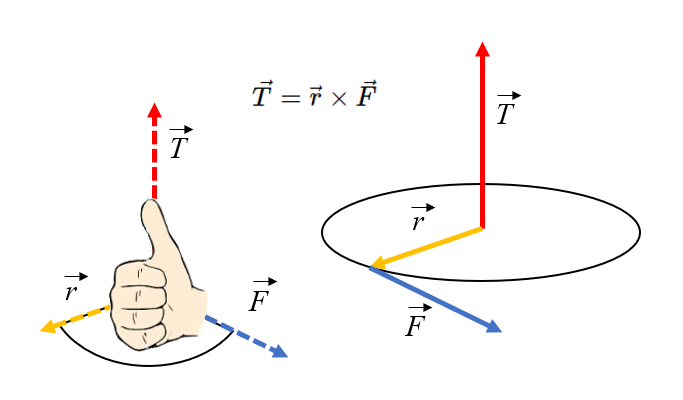
ID:(11602, 0)
Torque Generation
Model 
The torque is generated by a force applied at a certain distance from the axis of rotation. Forces on a point on the axis of rotation only lead to translation and do not induce changes in rotation or torque. The shortest distance between the point that attacks the force and the axis is called the arm and this is always perpendicular to the axis. A force parallel to the arm only generates shaft translation so that only the forces perpendicular to the arm generate torque. Finally it is seen that the torque is greater the greater the arm and the greater the force perpendicular to the arm.
Variables
Calculations
Calculations
Equations
(ID 3241)
In the case of a balance, a gravitational force acts on each arm, generating a torque
| $ T = r F $ |
If the lengths of the arms are $d_i$ and the forces are $F_i$ with $i=1,2$, the equilibrium condition requires that the sum of the torques be zero:
| $\displaystyle\sum_i \vec{T}_i=0$ |
Therefore, considering that the sign of each torque depends on the direction in which it induces rotation,
$d_1F_1-d_2F_2=0$
which results in
| $ d_1 F_1 = d_2 F_2 $ |
.
(ID 3250)
Si se deriva en el tiempo la relaci n para el momento angular
| $ L = r p $ |
para el caso de que el radio sea constante
$T=\displaystyle\frac{dL}{dt}=r\displaystyle\frac{dp}{dt}=rF$
por lo que
| $ T = r F $ |
(ID 4431)
Examples
As we have seen, torque plays a role analogous to force in the case of rotation:
$F\longleftrightarrow T$
To establish the equations of motion, we can recall how force was defined in terms of momentum:
$F=\displaystyle\frac{\Delta p}{\Delta t}$
and how torque was defined:
$T=\displaystyle\frac{\Delta L}{\Delta t}$
We can establish a relationship between the two to describe the generation of torque based on force:

Hence, we must first define what the equivalent of Momentum is in the context of rotation.
(ID 325)
If one considers the distribution of mass in space, it should always be possible to identify a point where the force exerted by the mass on one side is equal to the force generated on the other side:

This concept implies that for any orientation of an object, a point of support can be located, at which the object is in balance. Each of these points corresponds to a vertical line. By repeating this process with different orientations of the object, it eventually becomes evident that the vertical lines intersect at a particular point within the object. This point is referred to as the center of mass (CM). In essence, the center of mass is the unique point within the object where, regardless of its orientation, equilibrium is always achieved.
(ID 323)
One can define the center of mass as the point at which all the vertical lines drawn through points where the system is in equilibrium intersect:

(ID 11603)
Any object that both translates and rotates does so in a manner that:
• its translational motion can be described as if all the mass were concentrated at its center of mass,
• its rotation occurs around the center of mass as if it were not undergoing translation.

(ID 11604)
The orientation of torque can be determined using the right-hand rule: if you point your fingers in the direction of the radius and rotate in the direction of the force,

(ID 11602)
ID:(1416, 0)
