Physikalischen Pendels
Storyboard 
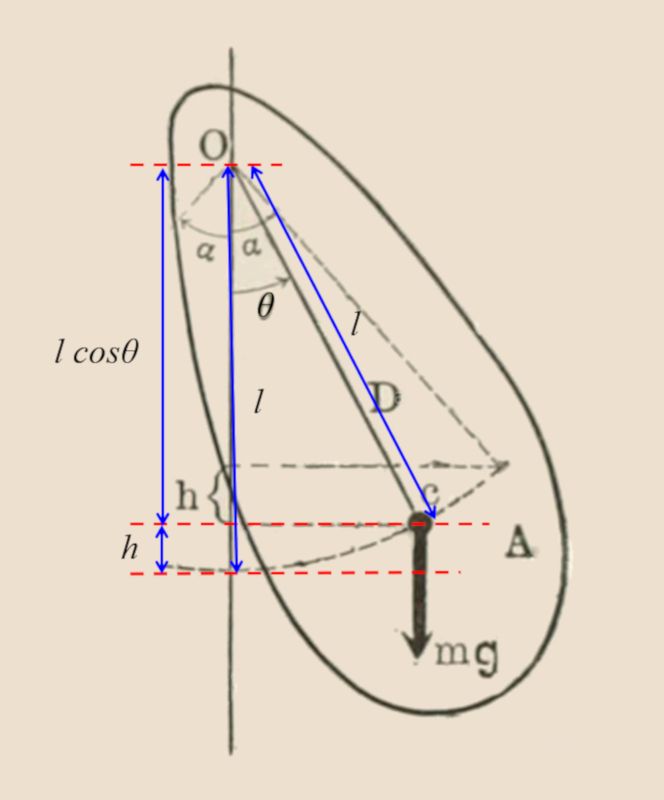
Bei einem Pendel aus einer realen Masse ergibt sich die potentielle Energie aus der Anhebung des Massenschwerpunkts gegen das Gravitationsfeld, wenn das Pendel um einen bestimmten Winkel abweicht.
ID:(1421, 0)
Physikalischen Pendels
Beschreibung 
Im Fall eines zusammengesetzten Pendels mit realer Masse wird die potenzielle Energie durch das Anheben des Schwerpunkts gegen das Gravitationsfeld erzeugt, wenn sich das Pendel um einen bestimmten Winkel auslenkt.
Variablen
Berechnungen
Berechnungen
Gleichungen
Die Arbeits Varianz ($\Delta W$), die erforderlich ist, damit ein Objekt von die Anfängliche Winkelgeschwindigkeit ($\omega_0$) auf die Winkelgeschwindigkeit ($\omega$) wechselt, wird durch das Anwenden eines der Drehmoment ($T$) erzeugt, das eine Winkelverschiebung die Differenz von Winkel ($\Delta\theta$) verursacht, gemäß:
| $ \Delta W = T \Delta\theta $ |
Anwendung des zweiten Newtonschen Gesetzes für Rotation in Bezug auf der Trägheitsmoment für Achse, die nicht durch das CM verläuft ($I$) und die Mittlere Winkelbeschleunigung ($\bar{\alpha}$):
| $ T = I \alpha $ |
kann dieser Ausdruck umgeschrieben werden als:
$\Delta W = I \alpha \Delta\theta$
oder unter Verwendung von die Unterschied in der Winkelgeschwindigkeiten ($\Delta\omega$) und der Abgelaufene Zeit ($\Delta t$):
| $ \bar{\alpha} \equiv \displaystyle\frac{ \Delta\omega }{ \Delta t }$ |
ergibt sich:
$\Delta W = I\displaystyle\frac{\Delta\omega}{\Delta t} \Delta\theta$
Durch Verwendung der Definition von die Mittlere Winkelgeschwindigkeit ($\bar{\omega}$) und der Abgelaufene Zeit ($\Delta t$):
| $ \bar{\omega} \equiv\displaystyle\frac{ \Delta\theta }{ \Delta t }$ |
resultiert:
$\Delta W = I\displaystyle\frac{\Delta\omega}{\Delta t} \Delta\theta = I\omega \Delta\omega$
wobei die Unterschied in der Winkelgeschwindigkeiten ($\Delta\omega$) sich ausdrückt als:
| $ \Delta\omega = \omega_2 - \omega_1 $ |
Andererseits kann die Winkelgeschwindigkeit durch die durchschnittliche Winkelgeschwindigkeit angenähert werden:
$\bar{\omega}=\displaystyle\frac{\omega_1 + \oemga_2}{2}$
Durch die Kombination beider Ausdrücke ergibt sich:
$\Delta W = I \omega \Delta\omega = I(\omega_2 - \omega_1) \displaystyle\frac{(\omega_1 + \omega_2)}{2} = \displaystyle\frac{I}{2}(\omega_2^2 - \omega_1^2)$
Daher ergibt sich der Energieänderungsausdruck:
$\Delta W = \displaystyle\frac{I}{2}\omega_2^2 - \displaystyle\frac{I}{2}\omega_1^2$
Damit kann die Rotationskinetik wie folgt definiert werden:
| $ K_r =\displaystyle\frac{1}{2} I \omega ^2$ |
(ID 3255)
(ID 3687)
Die potenzielle Gravitationsenergie eines Pendels mit Masse
| $ U = m g L (1-\cos \theta )$ |
wobei
F r kleine Winkel kann die Kosinus-Funktion durch eine Taylor-Reihenentwicklung bis zur zweiten Ordnung approximiert werden
$\cos\theta\sim 1-\displaystyle\frac{1}{2}\theta^2$
Diese N herung f hrt zu einer Vereinfachung der potenziellen Energie zu
| $ V =\displaystyle\frac{1}{2} m_g g L \theta ^2$ |
(ID 4514)
Da die Kinetische energie der rotation ($K_r$) des physikalischen Pendels in Abhängigkeit von der Trägheitsmoment für Achse, die nicht durch das CM verläuft ($I$) und die Winkelgeschwindigkeit ($\omega$) durch folgende Gleichung dargestellt wird:
| $ K_r =\displaystyle\frac{1}{2} I \omega ^2$ |
und die Potenzielle Energie Pendulum ($V$) in Funktion von die Gravitationsmasse ($m_g$), der Pendel Länge ($L$), der Schwenkwinkel ($\theta$) und die Gravitationsbeschleunigung ($g$) wie folgt ausgedrückt wird:
| $ V =\displaystyle\frac{1}{2} m_g g L \theta ^2$ |
lässt sich die Gleichung für die Gesamtenergie schreiben als:
$E = \displaystyle\frac{1}{2}I\omega^2 + \displaystyle\frac{1}{2}mgl\theta^2$
Da die Zeit ($T$) definiert ist als:
$T = 2\pi\sqrt{\displaystyle\frac{I}{mgl}}$
können wir die Winkelgeschwindigkeit bestimmen durch:
| $ \omega_0 ^2=\displaystyle\frac{ m g L }{ I }$ |
(ID 4517)
(ID 12338)
Mit der komplexen Zahl
| $ z = x_0 \cos \omega_0 t + i x_0 \sin \omega_0 t $ |
eingef hrt in
| $ \dot{z} = i \omega_0 z $ |
erhalten wir
$\dot{z} = i\omega_0 z = i \omega_0 x_0 \cos \omega_0 t - \omega_0 x_0 \sin \omega_0 t$
daher wird die Geschwindigkeit als der Realteil erhalten
| $ v = - x_0 \omega_0 \sin \omega_0 t $ |
(ID 14076)
Beispiele
(ID 15850)
Im Gegensatz zum mathematischen Pendel berücksichtigt das physikalische Pendel eine ausgedehnte die Gravitationsmasse ($m_g$) anstelle einer Punktmasse. Während der Pendel Länge ($L$) als der Abstand zwischen der Drehachse und dem Schwerpunkt des Körpers definiert wird wodurch die potenzielle Energie in beiden Modellen identisch ist , kann die Kinetische energie der rotation ($K_r$) nicht mehr mit Ausdrücken angenähert werden, die nur von der Pendel Länge ($L$) und die Gravitationsmasse ($m_g$) abhängen. In diesem Fall ist es unerlässlich, das tatsächliche der Trägheitsmoment für Achse, die nicht durch das CM verläuft ($I$) des Körpers zu kennen, um sein dynamisches Verhalten korrekt abzubilden.
(ID 7097)
Im Gegensatz zum mathematischen Pendel berücksichtigt das physikalische Pendel eine ausgedehnte die Gravitationsmasse ($m_g$) anstelle einer Punktmasse. Wenn der Pendel Länge ($L$) als der Abstand zwischen der Drehachse und dem Schwerpunkt des Körpers definiert wird, ist die Potenzielle Energie Pendulum ($V$) in beiden Modellen gleich. Allerdings kann die Kinetische energie der rotation ($K_r$) nicht mehr mit der Formel angenähert werden, die nur von der Pendel Länge ($L$) und die Gravitationsmasse ($m_g$) abhängt; sie muss das der Trägheitsmoment für Achse, die nicht durch das CM verläuft ($I$) des Körpers einbeziehen, um die Massenverteilung korrekt zu berücksichtigen.
(ID 1188)
(ID 15853)
ID:(1421, 0)
