Mit konstanter Winkelgeschwindigkeit abfangen
Storyboard 
Objekte können sich schneiden, wenn sie im gleichen Moment im Winkel übereinstimmen. Um dies zu erreichen, müssen sie sich von ihren jeweiligen Anfangswinkeln mit Winkelgeschwindigkeiten bewegen, die es ihnen ermöglichen, sich am Ende der Reise im Winkel und zur gleichen Zeit zu treffen.
ID:(1450, 0)
Mit konstanter Winkelgeschwindigkeit abfangen
Storyboard 
Objekte können sich schneiden, wenn sie im gleichen Moment im Winkel übereinstimmen. Um dies zu erreichen, müssen sie sich von ihren jeweiligen Anfangswinkeln mit Winkelgeschwindigkeiten bewegen, die es ihnen ermöglichen, sich am Ende der Reise im Winkel und zur gleichen Zeit zu treffen.
Variablen
Berechnungen
Berechnungen
Gleichungen
Im Fall, dass die Anfängliche Winkelgeschwindigkeit ($\omega_0$) gleich die Mittlere Winkelgeschwindigkeit ($\bar{\omega}$) ist,
Deshalb erhalten wir mit die Differenz von Winkel ($\Delta\theta$), welches gleich der Winkel ($\theta$) geteilt durch der Anfangswinkel ($\theta_0$) ist:
Und mit der Abgelaufene Zeit ($\Delta t$), welches gleich der Zeit ($t$) geteilt durch der Startzeit ($t_0$) ist:
Wir k nnen die Gleichung f r die Mittlere Winkelgeschwindigkeit ($\bar{\omega}$) umschreiben als:
Dies kann ausgedr ckt werden als:
$\omega_0 = \omega = \displaystyle\frac{\Delta\theta}{\Delta t} = \displaystyle\frac{\theta - \theta_0}{t - t_0}$
Bei der L sung erhalten wir:
Im Fall, dass die Anfängliche Winkelgeschwindigkeit ($\omega_0$) gleich die Mittlere Winkelgeschwindigkeit ($\bar{\omega}$) ist,
Deshalb erhalten wir mit die Differenz von Winkel ($\Delta\theta$), welches gleich der Winkel ($\theta$) geteilt durch der Anfangswinkel ($\theta_0$) ist:
Und mit der Abgelaufene Zeit ($\Delta t$), welches gleich der Zeit ($t$) geteilt durch der Startzeit ($t_0$) ist:
Wir k nnen die Gleichung f r die Mittlere Winkelgeschwindigkeit ($\bar{\omega}$) umschreiben als:
Dies kann ausgedr ckt werden als:
$\omega_0 = \omega = \displaystyle\frac{\Delta\theta}{\Delta t} = \displaystyle\frac{\theta - \theta_0}{t - t_0}$
Bei der L sung erhalten wir:
Da die Mittlere Geschwindigkeit ($\bar{v}$) mit die Zurückgelegte Strecke in einer Zeit ($\Delta s$) und der Abgelaufene Zeit ($\Delta t$) gleich ist, was ist
und mit die Zurückgelegte Strecke in einer Zeit ($\Delta s$) als Bogen eines Kreises und der Radius ($r$) und die Winkelvariation ($\Delta\theta$) ist
und die Definition von die Mittlere Winkelgeschwindigkeit ($\bar{\omega}$) ist
dann ist
$v=\displaystyle\frac{\Delta s}{\Delta t}=r\displaystyle\frac{\Delta\theta}{\Delta t}=r\omega$
Da die Beziehung allgemein ist, kann sie f r momentane Werte angewendet werden, was zu
f hrt.
Da die Mittlere Geschwindigkeit ($\bar{v}$) mit die Zurückgelegte Strecke in einer Zeit ($\Delta s$) und der Abgelaufene Zeit ($\Delta t$) gleich ist, was ist
und mit die Zurückgelegte Strecke in einer Zeit ($\Delta s$) als Bogen eines Kreises und der Radius ($r$) und die Winkelvariation ($\Delta\theta$) ist
und die Definition von die Mittlere Winkelgeschwindigkeit ($\bar{\omega}$) ist
dann ist
$v=\displaystyle\frac{\Delta s}{\Delta t}=r\displaystyle\frac{\Delta\theta}{\Delta t}=r\omega$
Da die Beziehung allgemein ist, kann sie f r momentane Werte angewendet werden, was zu
f hrt.
Die Definition von die Mittlere Winkelgeschwindigkeit ($\bar{\omega}$) wird als die Winkelvariation ($\Delta\theta$) betrachtet,
und der Abgelaufene Zeit ($\Delta t$),
Die Beziehung zwischen beiden wird als die Mittlere Winkelgeschwindigkeit ($\bar{\omega}$) definiert:
Die Definition von die Mittlere Winkelgeschwindigkeit ($\bar{\omega}$) wird als die Winkelvariation ($\Delta\theta$) betrachtet,
und der Abgelaufene Zeit ($\Delta t$),
Die Beziehung zwischen beiden wird als die Mittlere Winkelgeschwindigkeit ($\bar{\omega}$) definiert:
Beispiele
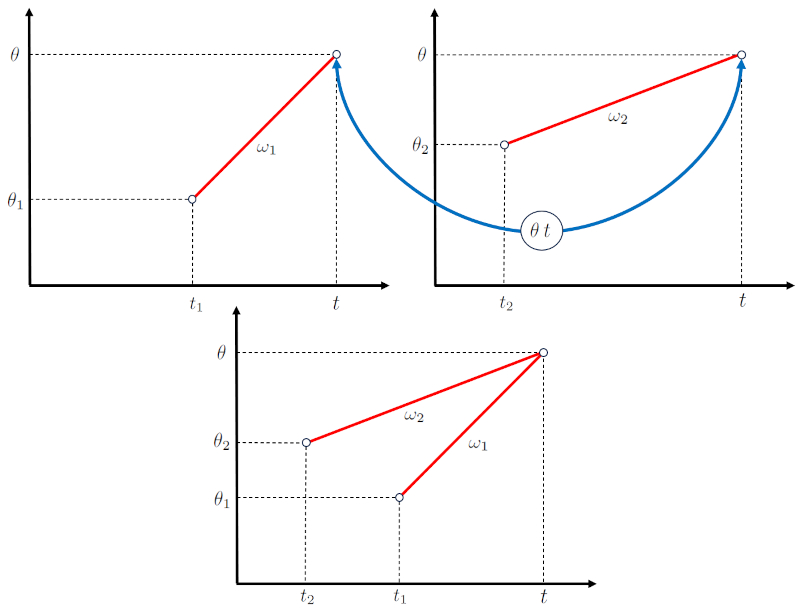
Im Falle einer Kreuzung bewegen sich zwei K rper so, dass sie sich zur Zeit ein Kreuzungszeit ($t$) an ERROR:10307,0 treffen werden.
Um dies zu erreichen, beginnt jeder K rper:
• Seine Verschiebung bei der Anfangszeit des ersten Objekts ($t_1$) bei der Anfangswinkel des ersten Körpers ($\theta_1$) mit eine Winkelgeschwindigkeit des Körpers 1 ($\omega_1$).
• Seine Verschiebung bei der Anfangszeit des zweiten Objekts ($t_2$) bei der Anfangswinkel des zweiten Körpers ($\theta_2$) mit eine Winkelgeschwindigkeit des Körpers 2 ($\omega_2$).
Diese Bedingungen m ssen erf llt sein, um die Kreuzung zu erreichen.
Die Winkel-Zeit-Diagramme k nnen dann wie folgt berlagert werden:
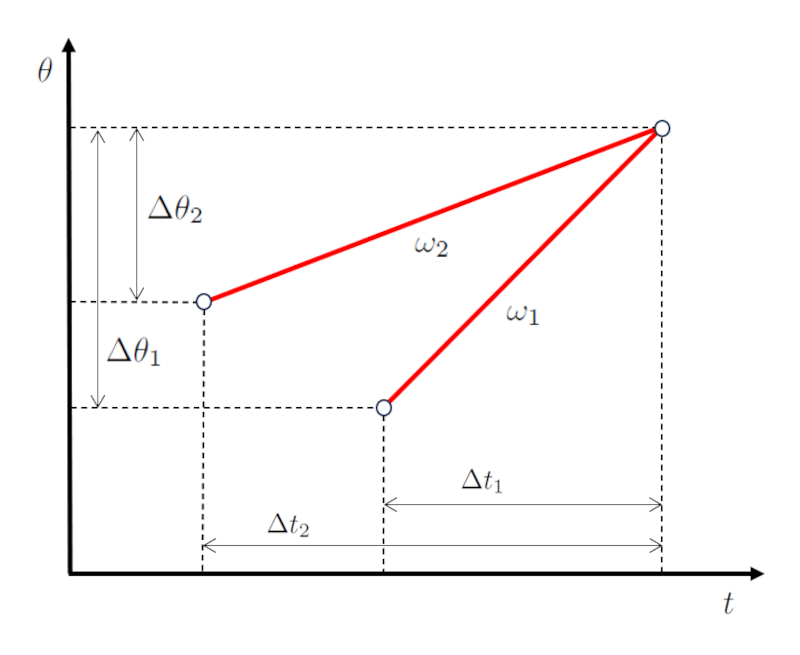
Im Falle einer Kreuzung oder Kollision zwischen zwei Objekten ist es blich, dass die Winkelgeschwindigkeit des Körpers 1 ($\omega_1$) und die Winkelgeschwindigkeit des Körpers 2 ($\omega_2$) so konfiguriert sind, dass sie zusammenfallen.
Das bedeutet, dass der Vom ersten Körper zurückgelegter Winkel ($\Delta\theta_1$) und die Reisezeit des ersten Objekts ($\Delta t_1$) zu eine Winkelgeschwindigkeit des Körpers 1 ($\omega_1$) f hren m ssen,
so dass mit der Vom zweiten Körper zurückgelegter Winkel ($\Delta\theta_2$) und die Reisezeit des zweiten Objekts ($\Delta t_2$) Eine Winkelgeschwindigkeit des Körpers 2 ($\omega_2$) erreicht wird,
damit sie schlie lich in Zeit und Raum (Position) bereinstimmen:
Im Fall einer Bewegung, bei der sich zwei Objekte schneiden, wie zum Beispiel die Kreuzungswinkel ($\theta$) und der Kreuzungszeit ($t$), ist dies f r beide blich. Daher, wenn f r das erste Objekt der Anfangszeit des ersten Objekts ($t_1$) und der Anfangswinkel des ersten Körpers ($\theta_1$) mit die Winkelgeschwindigkeit des Körpers 1 ($\omega_1$) erf llt sind:
und f r das zweite Objekt der Anfangszeit des zweiten Objekts ($t_2$) und der Anfangswinkel des zweiten Körpers ($\theta_2$) mit die Winkelgeschwindigkeit des Körpers 2 ($\omega_2$) erf llt sind:
was wie folgt dargestellt wird:
Um die Rotation eines Objekts zu beschreiben, m ssen wir die Winkelvariation ($\Delta\theta$) bestimmen. Dies geschieht, indem wir der Anfangswinkel ($\theta_0$) von der Winkel ($\theta$) subtrahieren, den Wert, den das Objekt w hrend seiner Rotation erreicht:
Um die Rotation eines Objekts zu beschreiben, m ssen wir die Winkelvariation ($\Delta\theta$) bestimmen. Dies geschieht, indem wir der Anfangswinkel ($\theta_0$) von der Winkel ($\theta$) subtrahieren, den Wert, den das Objekt w hrend seiner Rotation erreicht:
Um die Bewegung eines Objekts zu beschreiben, m ssen wir der Abgelaufene Zeit ($\Delta t$) berechnen. Diese Gr e wird durch Messung von der Startzeit ($t_0$) und der der Zeit ($t$) dieser Bewegung erhalten. Die Dauer wird bestimmt, indem die Anfangszeit von der Endzeit subtrahiert wird:
Um die Bewegung eines Objekts zu beschreiben, m ssen wir der Abgelaufene Zeit ($\Delta t$) berechnen. Diese Gr e wird durch Messung von der Startzeit ($t_0$) und der der Zeit ($t$) dieser Bewegung erhalten. Die Dauer wird bestimmt, indem die Anfangszeit von der Endzeit subtrahiert wird:
Im Fall, dass die Winkelgeschwindigkeit konstant ist, f llt die Mittlere Winkelgeschwindigkeit ($\bar{\omega}$) mit dem Wert von die Anfängliche Winkelgeschwindigkeit ($\omega_0$) zusammen, daher
In diesem Fall k nnen wir den Winkel als Funktion der Zeit berechnen, indem wir uns daran erinnern, dass er sich aus der Differenz zwischen dem aktuellen und dem Anfangswinkel sowie der aktuellen und der Anfangszeit ergibt. Daher ist der Winkel ($\theta$) gleich der Anfangswinkel ($\theta_0$), die Anfängliche Winkelgeschwindigkeit ($\omega_0$), der Zeit ($t$) und der Startzeit ($t_0$), wie unten gezeigt:
Die Gleichung stellt eine Gerade im Winkel-Zeit-Raum dar.
Im Fall, dass die Winkelgeschwindigkeit konstant ist, f llt die Mittlere Winkelgeschwindigkeit ($\bar{\omega}$) mit dem Wert von die Anfängliche Winkelgeschwindigkeit ($\omega_0$) zusammen, daher
In diesem Fall k nnen wir den Winkel als Funktion der Zeit berechnen, indem wir uns daran erinnern, dass er sich aus der Differenz zwischen dem aktuellen und dem Anfangswinkel sowie der aktuellen und der Anfangszeit ergibt. Daher ist der Winkel ($\theta$) gleich der Anfangswinkel ($\theta_0$), die Anfängliche Winkelgeschwindigkeit ($\omega_0$), der Zeit ($t$) und der Startzeit ($t_0$), wie unten gezeigt:
Die Gleichung stellt eine Gerade im Winkel-Zeit-Raum dar.
Um die Verschiebung eines Objekts zu sch tzen, ist es notwendig, seine die Winkelgeschwindigkeit ($\omega$) in Abh ngigkeit von der Zeit ($t$) zu kennen. Daher wird die die Mittlere Winkelgeschwindigkeit ($\bar{\omega}$) eingef hrt, die als das Verh ltnis zwischen die Winkelvariation ($\Delta\theta$) und der Abgelaufene Zeit ($\Delta t$) definiert ist.
Um dies zu messen, kann ein System wie das im Bild gezeigt verwendet werden:
Um die durchschnittliche Winkelgeschwindigkeit zu bestimmen, wird ein reflektierendes Element auf der Achse oder auf einer Scheibe mit mehreren reflektierenden Elementen platziert, und der Durchgang wird erfasst, um die L nge des Bogens $\Delta s$ und den Winkel, der mit dem Radius $r$ verbunden ist, zu sch tzen. Dann wird der Zeitunterschied aufgezeichnet, wenn die Markierung vor dem Sensor vorbeigeht, als $\Delta t$. Die durchschnittliche Winkelgeschwindigkeit wird durch die Division des zur ckgelegten Winkels durch die verstrichene Zeit bestimmt.
Die Gleichung, die die durchschnittliche Winkelgeschwindigkeit beschreibt, lautet:
Es ist zu beachten, dass die durchschnittliche Geschwindigkeit eine Sch tzung der tats chlichen Winkelgeschwindigkeit ist. Das Hauptproblem ist, dass:
Wenn sich die Winkelgeschwindigkeit w hrend der verstrichenen Zeit ndert, kann der Wert der durchschnittlichen Winkelgeschwindigkeit sehr unterschiedlich zur durchschnittlichen Winkelgeschwindigkeit sein.
Daher ist der Schl ssel:
Die Geschwindigkeit in einer ausreichend kurzen verstrichenen Zeit zu bestimmen, um ihre Variation zu minimieren.
Um die Verschiebung eines Objekts zu sch tzen, ist es notwendig, seine die Winkelgeschwindigkeit ($\omega$) in Abh ngigkeit von der Zeit ($t$) zu kennen. Daher wird die die Mittlere Winkelgeschwindigkeit ($\bar{\omega}$) eingef hrt, die als das Verh ltnis zwischen die Winkelvariation ($\Delta\theta$) und der Abgelaufene Zeit ($\Delta t$) definiert ist.
Um dies zu messen, kann ein System wie das im Bild gezeigt verwendet werden:
Um die durchschnittliche Winkelgeschwindigkeit zu bestimmen, wird ein reflektierendes Element auf der Achse oder auf einer Scheibe mit mehreren reflektierenden Elementen platziert, und der Durchgang wird erfasst, um die L nge des Bogens $\Delta s$ und den Winkel, der mit dem Radius $r$ verbunden ist, zu sch tzen. Dann wird der Zeitunterschied aufgezeichnet, wenn die Markierung vor dem Sensor vorbeigeht, als $\Delta t$. Die durchschnittliche Winkelgeschwindigkeit wird durch die Division des zur ckgelegten Winkels durch die verstrichene Zeit bestimmt.
Die Gleichung, die die durchschnittliche Winkelgeschwindigkeit beschreibt, lautet:
Es ist zu beachten, dass die durchschnittliche Geschwindigkeit eine Sch tzung der tats chlichen Winkelgeschwindigkeit ist. Das Hauptproblem ist, dass:
Wenn sich die Winkelgeschwindigkeit w hrend der verstrichenen Zeit ndert, kann der Wert der durchschnittlichen Winkelgeschwindigkeit sehr unterschiedlich zur durchschnittlichen Winkelgeschwindigkeit sein.
Daher ist der Schl ssel:
Die Geschwindigkeit in einer ausreichend kurzen verstrichenen Zeit zu bestimmen, um ihre Variation zu minimieren.
Wenn wir das Verh ltnis zwischen die Zurückgelegte Strecke in einer Zeit ($\Delta s$) und der Radius ($r$) durch die Winkelvariation ($\Delta\theta$) teilen,
und das dann durch der Abgelaufene Zeit ($\Delta t$) teilen, erhalten wir die Beziehung, die es uns erm glicht, die Geschwindigkeit ($v$) entlang der Umlaufbahn zu berechnen, bekannt als die tangentielle Geschwindigkeit, die mit die Winkelgeschwindigkeit ($\omega$) verbunden ist:
Wenn wir das Verh ltnis zwischen die Zurückgelegte Strecke in einer Zeit ($\Delta s$) und der Radius ($r$) durch die Winkelvariation ($\Delta\theta$) teilen,
und das dann durch der Abgelaufene Zeit ($\Delta t$) teilen, erhalten wir die Beziehung, die es uns erm glicht, die Geschwindigkeit ($v$) entlang der Umlaufbahn zu berechnen, bekannt als die tangentielle Geschwindigkeit, die mit die Winkelgeschwindigkeit ($\omega$) verbunden ist:
ID:(1450, 0)