Konstante Winkelbeschleunigung, zwei Stufen
Storyboard 
Im Falle einer beschleunigten Winkelbewegung in zwei Phasen wird beim Übergang von der ersten zur zweiten Winkelbeschleunigung die Endwinkelgeschwindigkeit der ersten Phase zur Anfangswinkelgeschwindigkeit der zweiten Phase. Das Gleiche gilt für den Winkel, wobei der Endwinkel der ersten Phase dem Anfangswinkel der zweiten Phase entspricht.
Im Gegensatz zum Modell mit zwei Winkelgeschwindigkeiten weist dieses Modell keine Diskontinuitätsprobleme auf, außer dass die Winkelbeschleunigung sich abrupt ändern kann, was technisch möglich ist, aber oft nicht sehr realistisch ist.
ID:(1409, 0)
Konstante Winkelbeschleunigung, zwei Stufen
Storyboard 
Im Falle einer beschleunigten Winkelbewegung in zwei Phasen wird beim Übergang von der ersten zur zweiten Winkelbeschleunigung die Endwinkelgeschwindigkeit der ersten Phase zur Anfangswinkelgeschwindigkeit der zweiten Phase. Das Gleiche gilt für den Winkel, wobei der Endwinkel der ersten Phase dem Anfangswinkel der zweiten Phase entspricht. Im Gegensatz zum Modell mit zwei Winkelgeschwindigkeiten weist dieses Modell keine Diskontinuitätsprobleme auf, außer dass die Winkelbeschleunigung sich abrupt ändern kann, was technisch möglich ist, aber oft nicht sehr realistisch ist.
Variablen
Berechnungen
Berechnungen
Gleichungen
Die Definition der durchschnittlichen Winkelbeschleunigung basiert auf dem zur ckgelegten Winkel
und der verstrichenen Zeit
Die Beziehung zwischen beiden wird als die durchschnittliche Winkelbeschleunigung definiert
innerhalb dieses Zeitintervalls.
Die Definition der durchschnittlichen Winkelbeschleunigung basiert auf dem zur ckgelegten Winkel
und der verstrichenen Zeit
Die Beziehung zwischen beiden wird als die durchschnittliche Winkelbeschleunigung definiert
innerhalb dieses Zeitintervalls.
Angesichts dessen, dass die Mittlere Beschleunigung ($\bar{a}$) gleich die Geschwindigkeit Unterschied ($\Delta v$) und der Abgelaufene Zeit ($\Delta t$) gem
und die Mittlere Winkelbeschleunigung ($\bar{\alpha}$) gleich die Unterschied in der Winkelgeschwindigkeiten ($\Delta\omega$) und der Abgelaufene Zeit ($\Delta t$) laut
ist, folgt daraus, dass
$\bar{a}=\displaystyle\frac{\Delta v}{\Delta t}=r\displaystyle\frac{\Delta\omega}{\Delta t}=\bar{\alpha}$
Unter der Annahme, dass die Mittlere Winkelbeschleunigung ($\bar{\alpha}$) gleich die Constant Angular Acceleration ($\alpha_0$) ist
und angenommen, dass die Mittlere Beschleunigung ($\bar{a}$) gleich die konstante Beschleunigung ($a_0$) ist
ergibt sich folgende Gleichung:
Angesichts dessen, dass die Mittlere Beschleunigung ($\bar{a}$) gleich die Geschwindigkeit Unterschied ($\Delta v$) und der Abgelaufene Zeit ($\Delta t$) gem
und die Mittlere Winkelbeschleunigung ($\bar{\alpha}$) gleich die Unterschied in der Winkelgeschwindigkeiten ($\Delta\omega$) und der Abgelaufene Zeit ($\Delta t$) laut
ist, folgt daraus, dass
$\bar{a}=\displaystyle\frac{\Delta v}{\Delta t}=r\displaystyle\frac{\Delta\omega}{\Delta t}=\bar{\alpha}$
Unter der Annahme, dass die Mittlere Winkelbeschleunigung ($\bar{\alpha}$) gleich die Constant Angular Acceleration ($\alpha_0$) ist
und angenommen, dass die Mittlere Beschleunigung ($\bar{a}$) gleich die konstante Beschleunigung ($a_0$) ist
ergibt sich folgende Gleichung:
Wenn wir annehmen, dass die Mittlere Winkelbeschleunigung ($\bar{\alpha}$) konstant und gleich die Constant Angular Acceleration ($\alpha_0$) ist, dann gilt die folgende Gleichung:
Daher, unter Ber cksichtigung von die Unterschied in der Winkelgeschwindigkeiten ($\Delta\omega$) zusammen mit die Winkelgeschwindigkeit ($\omega$) und die Anfängliche Winkelgeschwindigkeit ($\omega_0$):
und der Abgelaufene Zeit ($\Delta t$) in Bezug auf der Zeit ($t$) und der Startzeit ($t_0$):
kann die Gleichung f r die Mittlere Winkelbeschleunigung ($\bar{\alpha}$):
wie folgt ausgedr ckt werden:
$\alpha_0 = \alpha = \displaystyle\frac{\Delta \omega}{\Delta t} = \displaystyle\frac{\omega - \omega_0}{t - t_0}$
Durch Aufl sen erhalten wir:
Wenn wir annehmen, dass die Mittlere Winkelbeschleunigung ($\bar{\alpha}$) konstant und gleich die Constant Angular Acceleration ($\alpha_0$) ist, dann gilt die folgende Gleichung:
Daher, unter Ber cksichtigung von die Unterschied in der Winkelgeschwindigkeiten ($\Delta\omega$) zusammen mit die Winkelgeschwindigkeit ($\omega$) und die Anfängliche Winkelgeschwindigkeit ($\omega_0$):
und der Abgelaufene Zeit ($\Delta t$) in Bezug auf der Zeit ($t$) und der Startzeit ($t_0$):
kann die Gleichung f r die Mittlere Winkelbeschleunigung ($\bar{\alpha}$):
wie folgt ausgedr ckt werden:
$\alpha_0 = \alpha = \displaystyle\frac{\Delta \omega}{\Delta t} = \displaystyle\frac{\omega - \omega_0}{t - t_0}$
Durch Aufl sen erhalten wir:
Im Fall von die Constant Angular Acceleration ($\alpha_0$) folgt die Winkelgeschwindigkeit ($\omega$) als Funktion von der Zeit ($t$) einer linearen Beziehung mit der Startzeit ($t_0$) und die Anfängliche Winkelgeschwindigkeit ($\omega_0$) in der Form:
Da der zur ckgelegte Winkel gleich der Fl che unter der Kurve der Winkelgeschwindigkeit-Zeit ist, kann in diesem Fall der Beitrag des Rechtecks:
$\omega_0(t-t_0)$
und des Dreiecks:
$\displaystyle\frac{1}{2}\alpha_0(t-t_0)^2$
hinzugef gt werden.
Dies f hrt uns zu dem Ausdruck f r der Winkel ($\theta$) und der Anfangswinkel ($\theta_0$):
Im Fall von die Constant Angular Acceleration ($\alpha_0$) folgt die Winkelgeschwindigkeit ($\omega$) als Funktion von der Zeit ($t$) einer linearen Beziehung mit der Startzeit ($t_0$) und die Anfängliche Winkelgeschwindigkeit ($\omega_0$) in der Form:
Da der zur ckgelegte Winkel gleich der Fl che unter der Kurve der Winkelgeschwindigkeit-Zeit ist, kann in diesem Fall der Beitrag des Rechtecks:
$\omega_0(t-t_0)$
und des Dreiecks:
$\displaystyle\frac{1}{2}\alpha_0(t-t_0)^2$
hinzugef gt werden.
Dies f hrt uns zu dem Ausdruck f r der Winkel ($\theta$) und der Anfangswinkel ($\theta_0$):
Wenn wir die Zeit in der Gleichung von die Winkelgeschwindigkeit ($\omega$) aufl sen, die die Variablen die Anfängliche Winkelgeschwindigkeit ($\omega_0$), der Zeit ($t$), der Startzeit ($t_0$) und die Constant Angular Acceleration ($\alpha_0$) umfasst:
erhalten wir den folgenden Ausdruck f r die Zeit:
$t - t_0 = \displaystyle\frac{\omega - \omega_0}{\alpha_0}$
Diese L sung kann in die Gleichung eingesetzt werden, um der Winkel ($\theta$) unter Verwendung von der Anfangswinkel ($\theta_0$) wie folgt zu berechnen:
was in der folgenden Gleichung resultiert:
Wenn wir die Zeit in der Gleichung von die Winkelgeschwindigkeit ($\omega$) aufl sen, die die Variablen die Anfängliche Winkelgeschwindigkeit ($\omega_0$), der Zeit ($t$), der Startzeit ($t_0$) und die Constant Angular Acceleration ($\alpha_0$) umfasst:
erhalten wir den folgenden Ausdruck f r die Zeit:
$t - t_0 = \displaystyle\frac{\omega - \omega_0}{\alpha_0}$
Diese L sung kann in die Gleichung eingesetzt werden, um der Winkel ($\theta$) unter Verwendung von der Anfangswinkel ($\theta_0$) wie folgt zu berechnen:
was in der folgenden Gleichung resultiert:
Beispiele
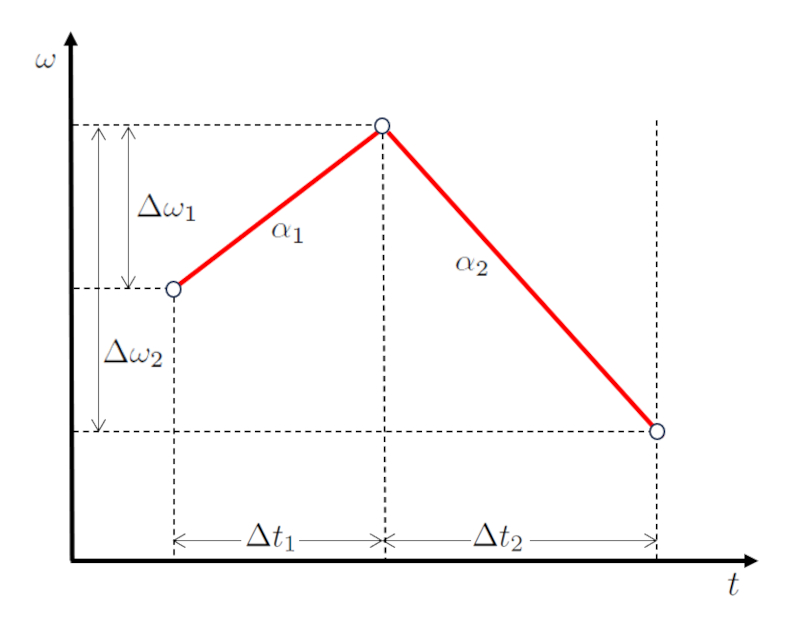
In einem Szenario mit zweistufiger Bewegung passt das Objekt zun chst seine Geschwindigkeit um den Unterschied von die Variation der Winkelgeschwindigkeiten in der ersten Stufe ($\Delta\omega_1$) ber einen Zeitraum von der In der ersten Phase verstrichene Zeit ($\Delta t_1$) an und erf hrt dabei eine Beschleunigung von die Winkelbeschleunigung während der ersten Stufe ($\alpha_1$).
In der zweiten Stufe ndert das Objekt seine Geschwindigkeit weiterhin um die Variation der Winkelgeschwindigkeiten in der zweiten Stufe ($\Delta\omega_2$) ber einen Zeitraum von der In der zweiten Phase verbrachte Zeit ($\Delta t_2$) mit einer Beschleunigung von die Winkelbeschleunigung während der zweiten Stufe ($\alpha_2$).
Graphisch dargestellt ergibt dies ein Geschwindigkeits-Zeit-Diagramm, wie unten gezeigt:
Es ist wichtig zu beachten, dass die Zeitintervalle der In der ersten Phase verstrichene Zeit ($\Delta t_1$) und der In der zweiten Phase verbrachte Zeit ($\Delta t_2$) aufeinanderfolgend sind, ebenso wie die Geschwindigkeits nderungen die Variation der Winkelgeschwindigkeiten in der ersten Stufe ($\Delta\omega_1$) und die Variation der Winkelgeschwindigkeiten in der zweiten Stufe ($\Delta\omega_2$).
Bei der Analyse einer in zwei Phasen segmentierten Bewegung ist die erste Phase durch eine lineare Funktion gekennzeichnet, die die Punkte der Startzeit ($t_0$), der Endzeit der ersten und Beginn der zweiten Etappe ($t_1$), die Anfängliche Winkelgeschwindigkeit ($\omega_0$) und die Erste Endwinkelgeschwindigkeit und Beginn der zweiten Stufe ($\omega_1$) umfasst. Diese wird durch eine Gerade mit der Steigung die Winkelbeschleunigung während der ersten Stufe ($\alpha_1$) ausgedr ckt, deren mathematische Beziehung in der folgenden Gleichung spezifiziert ist:
Beim bergang zur zweiten Phase, die durch die Punkte die Erste Endwinkelgeschwindigkeit und Beginn der zweiten Stufe ($\omega_1$), die Endwinkelgeschwindigkeit der zweiten Stufe ($\omega_2$), der Endzeit der ersten und Beginn der zweiten Etappe ($t_1$) und der Endzeit der zweiten Etappe ($t_2$) definiert wird, wird eine neue lineare Funktion mit einer Steigung von die Winkelbeschleunigung während der zweiten Stufe ($\alpha_2$) bernommen. Diese Beziehung wird durch die zweite vorgestellte Gleichung dargelegt:
Die grafische Darstellung dieser linearen Beziehungen wird unten illustriert und bietet eine klare Visualisierung, wie sich die Steigung zwischen den beiden Phasen ver ndert:
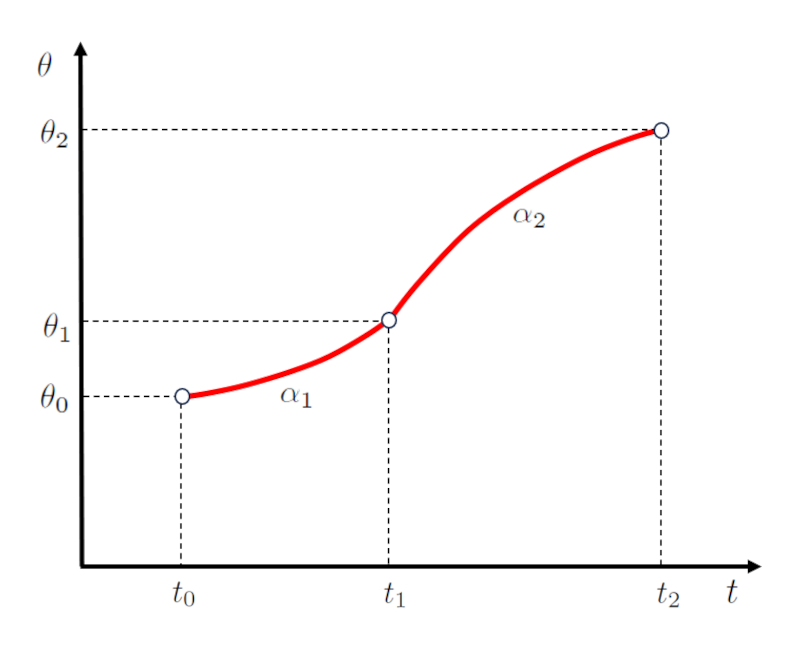
In einem Szenario mit einer Bewegung, die in zwei Phasen unterteilt ist, entspricht der Winkel am Ende der ersten Phase dem Winkel am Anfang der zweiten Phase, gekennzeichnet als der Der erste Schlusswinkel und die zweite Etappe begannen ($\theta_1$).
Ebenso f llt der Zeitpunkt, an dem die erste Phase endet, mit dem Beginn der zweiten Phase zusammen, markiert durch der Endzeit der ersten und Beginn der zweiten Etappe ($t_1$).
Da die Bewegung durch die erfahrene Winkelbeschleunigung definiert wird, muss die Winkelgeschwindigkeit am Ende der ersten Phase mit der Anfangswinkelgeschwindigkeit der zweiten Phase bereinstimmen, angezeigt durch die Erste Endwinkelgeschwindigkeit und Beginn der zweiten Stufe ($\omega_1$).
Im Kontext einer konstanten Winkelbeschleunigung wird der Winkel bei der Der erste Schlusswinkel und die zweite Etappe begannen ($\theta_1$) durch die Variablen der Anfangswinkel ($\theta_0$), die Anfängliche Winkelgeschwindigkeit ($\omega_0$), die Winkelbeschleunigung während der ersten Stufe ($\alpha_1$), der Endzeit der ersten und Beginn der zweiten Etappe ($t_1$) und der Startzeit ($t_0$) bestimmt, wie in der folgenden Gleichung gezeigt:
In der zweiten Phase wird der Winkel bei die Endwinkel der zweiten Stufe ($\theta_2$) basierend auf der Der erste Schlusswinkel und die zweite Etappe begannen ($\theta_1$), die Erste Endwinkelgeschwindigkeit und Beginn der zweiten Stufe ($\omega_1$), die Winkelbeschleunigung während der zweiten Stufe ($\alpha_2$), der Endzeit der ersten und Beginn der zweiten Etappe ($t_1$) und der Endzeit der zweiten Etappe ($t_2$) berechnet, gem :
Die grafische Darstellung dieser Beziehungen wird unten illustriert:
Die Rate, mit der sich die Winkelgeschwindigkeit im Laufe der Zeit ndert, wird als die Mittlere Winkelbeschleunigung ($\bar{\alpha}$) definiert. Um dies zu messen, m ssen wir die Unterschied in der Winkelgeschwindigkeiten ($\Delta\omega$) und der Abgelaufene Zeit ($\Delta t$) beobachten.
Die Gleichung, die die Mittlere Winkelbeschleunigung ($\bar{\alpha}$) beschreibt, lautet wie folgt:
Die Rate, mit der sich die Winkelgeschwindigkeit im Laufe der Zeit ndert, wird als die Mittlere Winkelbeschleunigung ($\bar{\alpha}$) definiert. Um dies zu messen, m ssen wir die Unterschied in der Winkelgeschwindigkeiten ($\Delta\omega$) und der Abgelaufene Zeit ($\Delta t$) beobachten.
Die Gleichung, die die Mittlere Winkelbeschleunigung ($\bar{\alpha}$) beschreibt, lautet wie folgt:
Um die Rotation eines Objekts zu beschreiben, m ssen wir die Winkelvariation ($\Delta\theta$) bestimmen. Dies geschieht, indem wir der Anfangswinkel ($\theta_0$) von der Winkel ($\theta$) subtrahieren, den Wert, den das Objekt w hrend seiner Rotation erreicht:
Um die Rotation eines Objekts zu beschreiben, m ssen wir die Winkelvariation ($\Delta\theta$) bestimmen. Dies geschieht, indem wir der Anfangswinkel ($\theta_0$) von der Winkel ($\theta$) subtrahieren, den Wert, den das Objekt w hrend seiner Rotation erreicht:
Die Beschleunigung wird als nderung der Winkelgeschwindigkeit pro Zeiteinheit definiert.
Daher kann die Winkelbeschleunigung die Unterschied in der Winkelgeschwindigkeiten ($\Delta\omega$) in Bezug auf die Winkelgeschwindigkeit die Winkelgeschwindigkeit ($\omega$) und die Zeit die Anfängliche Winkelgeschwindigkeit ($\omega_0$) wie folgt ausgedr ckt werden:
Die Beschleunigung wird als nderung der Winkelgeschwindigkeit pro Zeiteinheit definiert.
Daher kann die Winkelbeschleunigung die Unterschied in der Winkelgeschwindigkeiten ($\Delta\omega$) in Bezug auf die Winkelgeschwindigkeit die Winkelgeschwindigkeit ($\omega$) und die Zeit die Anfängliche Winkelgeschwindigkeit ($\omega_0$) wie folgt ausgedr ckt werden:
Um die Bewegung eines Objekts zu beschreiben, m ssen wir der Abgelaufene Zeit ($\Delta t$) berechnen. Diese Gr e wird durch Messung von der Startzeit ($t_0$) und der der Zeit ($t$) dieser Bewegung erhalten. Die Dauer wird bestimmt, indem die Anfangszeit von der Endzeit subtrahiert wird:
Um die Bewegung eines Objekts zu beschreiben, m ssen wir der Abgelaufene Zeit ($\Delta t$) berechnen. Diese Gr e wird durch Messung von der Startzeit ($t_0$) und der der Zeit ($t$) dieser Bewegung erhalten. Die Dauer wird bestimmt, indem die Anfangszeit von der Endzeit subtrahiert wird:
Mit die Constant Angular Acceleration ($\alpha_0$) stellt die Winkelgeschwindigkeit ($\omega$) eine lineare Beziehung mit der Zeit ($t$) her, die auch die Variablen die Anfängliche Winkelgeschwindigkeit ($\omega_0$) und der Startzeit ($t_0$) einbezieht, wie folgt:
Diese Gleichung repr sentiert eine Gerade im Raum der Winkelgeschwindigkeit gegen ber der Zeit.
Mit die Constant Angular Acceleration ($\alpha_0$) stellt die Winkelgeschwindigkeit ($\omega$) eine lineare Beziehung mit der Zeit ($t$) her, die auch die Variablen die Anfängliche Winkelgeschwindigkeit ($\omega_0$) und der Startzeit ($t_0$) einbezieht, wie folgt:
Diese Gleichung repr sentiert eine Gerade im Raum der Winkelgeschwindigkeit gegen ber der Zeit.
Da der gesamte Weg der Fl che unter der Kurve der Winkelgeschwindigkeit gegen ber der Zeit entspricht, ergibt sich im Fall von eine Constant Angular Acceleration ($\alpha_0$), dass der Weg der Winkel ($\theta$) mit den Variablen der Anfangswinkel ($\theta_0$), der Zeit ($t$), der Startzeit ($t_0$) und die Anfängliche Winkelgeschwindigkeit ($\omega_0$) wie folgt ist:
Diese Ausdruck entspricht der allgemeinen Form einer Parabel.
Da der gesamte Weg der Fl che unter der Kurve der Winkelgeschwindigkeit gegen ber der Zeit entspricht, ergibt sich im Fall von eine Constant Angular Acceleration ($\alpha_0$), dass der Weg der Winkel ($\theta$) mit den Variablen der Anfangswinkel ($\theta_0$), der Zeit ($t$), der Startzeit ($t_0$) und die Anfängliche Winkelgeschwindigkeit ($\omega_0$) wie folgt ist:
Diese Ausdruck entspricht der allgemeinen Form einer Parabel.
Im Fall von die Constant Angular Acceleration ($\alpha_0$) wird die Funktion von die Winkelgeschwindigkeit ($\omega$) bez glich der Zeit ($t$), zusammen mit den zus tzlichen Variablen die Anfängliche Winkelgeschwindigkeit ($\omega_0$) und der Startzeit ($t_0$), durch die Gleichung ausgedr ckt:
Aus dieser Gleichung l sst sich die Beziehung zwischen der Winkel ($\theta$) und der Anfangswinkel ($\theta_0$) sowie die Ver nderung der Winkelgeschwindigkeit berechnen:
Im Fall von die Constant Angular Acceleration ($\alpha_0$) wird die Funktion von die Winkelgeschwindigkeit ($\omega$) bez glich der Zeit ($t$), zusammen mit den zus tzlichen Variablen die Anfängliche Winkelgeschwindigkeit ($\omega_0$) und der Startzeit ($t_0$), durch die Gleichung ausgedr ckt:
Aus dieser Gleichung l sst sich die Beziehung zwischen der Winkel ($\theta$) und der Anfangswinkel ($\theta_0$) sowie die Ver nderung der Winkelgeschwindigkeit berechnen:
Wenn wir das Verh ltnis zwischen die Mittlere Geschwindigkeit ($\bar{v}$), der Radio ($r$) und die Mittlere Winkelgeschwindigkeit ($\bar{\omega}$), das in der folgenden Gleichung dargestellt ist:
durch den Wert von der Abgelaufene Zeit ($\Delta t$) teilen, k nnen wir den Faktor ermitteln, der es uns erm glicht, die Winkelbeschleunigung entlang der Umlaufbahn zu berechnen:
Wenn wir das Verh ltnis zwischen die Mittlere Geschwindigkeit ($\bar{v}$), der Radio ($r$) und die Mittlere Winkelgeschwindigkeit ($\bar{\omega}$), das in der folgenden Gleichung dargestellt ist:
durch den Wert von der Abgelaufene Zeit ($\Delta t$) teilen, k nnen wir den Faktor ermitteln, der es uns erm glicht, die Winkelbeschleunigung entlang der Umlaufbahn zu berechnen:
ID:(1409, 0)