Conversor trabalho-calor
Imagem 
A conversão de trabalho em energia é estudada através da geração de calor por meio do atrito. Para isso, envolve-se uma faixa metálica ao redor de um cilindro que contém água e um termômetro. Ao girar a manivela, o atrito gera calor, levando ao aquecimento da água. Se medirmos a força aplicada, o número de voltas realizadas e o raio do cilindro, é possível estimar a distância percorrida, o que nos permite estimar a energia como o produto da força pela distância.

ID:(1884, 0)
Definição de caminho
Nota 
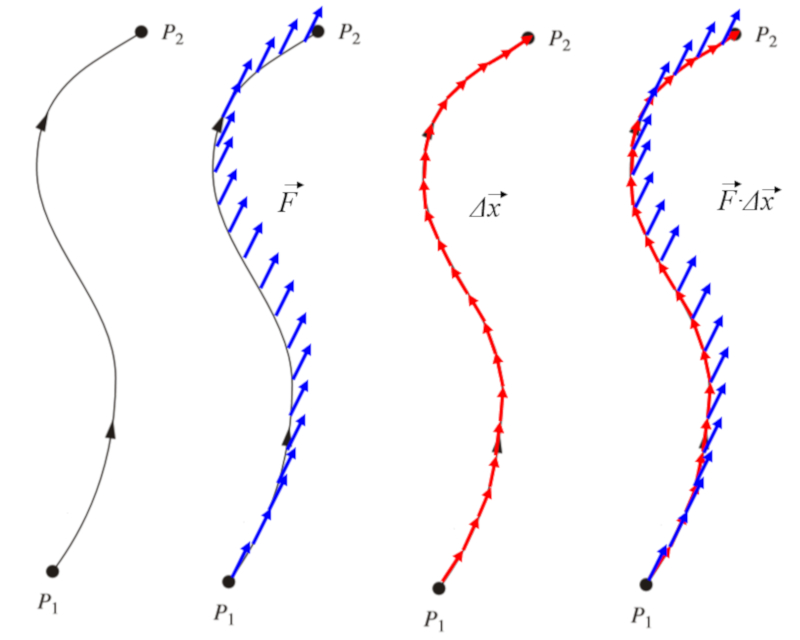
Para qualquer trajeto dado, é possível definir a força atuante em cada ponto. Além disso, se dividirmos esse trajeto em segmentos distintos representados pelos vetores $d\vec{x}$, podemos calcular o produto escalar entre eles para determinar a energia que está sendo consumida:
ID:(11514, 0)
