Rotational kinetic energy and moments of inertia
Storyboard 
The kinetic energy of rotation is a function of the angular velocity achieved through the application of torque over a given time while traversing a given angle.Thus, rotational kinetic energy is proportional to the moment of inertia of the object and the square of the angular velocity.
ID:(1417, 0)
Bar that rotates around an axis $\perp$
Image 
A bar with mass $m$ and length $l$ rotating around its center, which coincides with the center of mass:
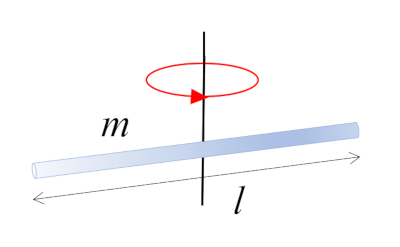
ID:(10962, 0)
Cylinder rotating around axis $\parallel$
Image 
A rotation of a cylinder with mass $m$ and radius $r$ around the axis of the cylinder, where the center of mass (CM) is located at mid-height:
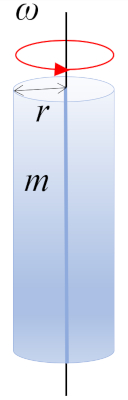
ID:(10964, 0)
Cylinder that rotates about axis $\perp$
Image 
In this scenario, a cylinder with mass $m$, radius $r$, and height $h$ is rotating around an axis perpendicular to its own axis. This axis passes through the midpoint of the cylinder's length, where the center of mass (CM) is located:
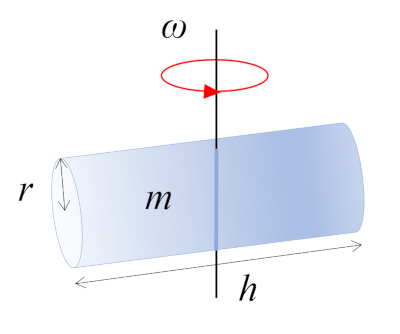
ID:(10965, 0)
Sphere
Image 
A sphere with mass $m$ and radius $r$ is rotating around its center of mass, which is located at its geometric center:
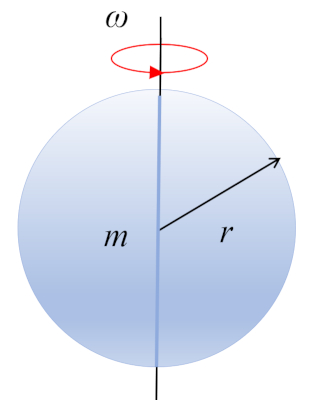
ID:(10490, 0)
Regular parallelepiped moment of inertia
Image 
A straight rectangular parallelepiped with mass $m$ and sides $a$ and $b$, perpendicular to the axis of rotation, is rotating around its center of mass, which is located at the geometric center of the body:
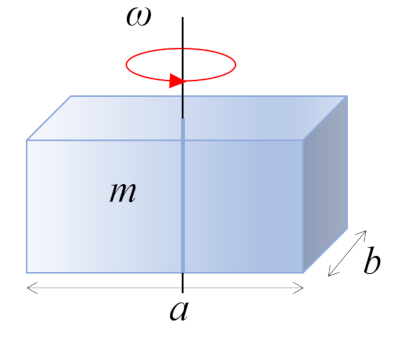
ID:(10973, 0)
Straight parallelepiped
Image 
In the case of a right rectangular parallelepiped with mass $m$ and side $a$, the center of mass is located at the geometric center:
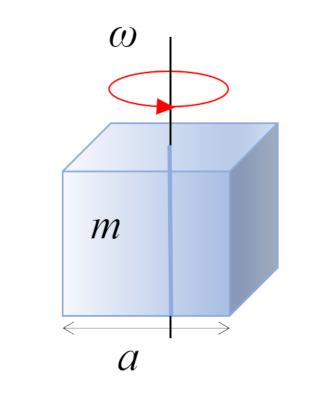
ID:(10963, 0)
Moment of inertia
Description 
In rotational dynamics, the moment of inertia plays a role equivalent to that of inertial mass in translational motion. However, unlike mass, the moment of inertia depends on the geometry of the body and how its mass is distributed with respect to the axis of rotation. Therefore, its calculation is essential for each situation that is intended to be modeled.
Variables
Calculations
Calculations
Equations
The work variance ($\Delta W$) required for an object to change from the initial Angular Speed ($\omega_0$) to the angular Speed ($\omega$) is obtained by applying a the torque ($T$) that produces an angular displacement the difference of Angles ($\Delta\theta$), according to:
| $ \Delta W = T \Delta\theta $ |
Applying Newton's second law for rotation, in terms of the moment of inertia for axis that does not pass through the CM ($I$) and the mean Angular Acceleration ($\bar{\alpha}$):
| $ T = I \alpha $ |
this expression can be rewritten as:
$\Delta W = I \alpha \Delta\theta$
or, using the difference in Angular Speeds ($\Delta\omega$) and the time elapsed ($\Delta t$):
| $ \bar{\alpha} \equiv \displaystyle\frac{ \Delta\omega }{ \Delta t }$ |
we get:
$\Delta W = I\displaystyle\frac{\Delta\omega}{\Delta t} \Delta\theta$
Using the definition of the mean angular velocity ($\bar{\omega}$) and the time elapsed ($\Delta t$):
| $ \bar{\omega} \equiv\displaystyle\frac{ \Delta\theta }{ \Delta t }$ |
results in:
$\Delta W = I\displaystyle\frac{\Delta\omega}{\Delta t} \Delta\theta = I\omega \Delta\omega$
where the difference in Angular Speeds ($\Delta\omega$) is expressed as:
| $ \Delta\omega = \omega_2 - \omega_1 $ |
On the other hand, the angular velocity can be approximated by the average angular velocity:
$\bar{\omega}=\displaystyle\frac{\omega_1 + \oemga_2}{2}$
By combining both expressions, we obtain the equation:
$\Delta W = I \omega \Delta\omega = I(\omega_2 - \omega_1) \displaystyle\frac{(\omega_1 + \omega_2)}{2} = \displaystyle\frac{I}{2}(\omega_2^2 - \omega_1^2)$
Therefore, the change in energy is expressed as:
$\Delta W = \displaystyle\frac{I}{2}\omega_2^2 - \displaystyle\frac{I}{2}\omega_1^2$
This allows us to define the rotational kinetic energy as:
| $ K_r =\displaystyle\frac{1}{2} I \omega ^2$ |
(ID 3255)
The moment of inertia of a rod rotating around a perpendicular ($\perp$) axis passing through the center is obtained by dividing the body into small volumes and summing them:
| $ I =\displaystyle\int_V r ^2 \rho dV $ |
resulting in
(ID 4432)
The moment of inertia of a parallelepiped rotating around an axis passing through its center is obtained by partitioning the body into small volumes and summing them up:
| $ I =\displaystyle\int_V r ^2 \rho dV $ |
resulting in
| $ I_{CM} =\displaystyle\frac{1}{12} m ( a ^2+ b ^2)$ |
.
(ID 4433)
The moment of inertia of a cylinder rotating around an axis parallel ($\parallel$) to its central axis is obtained by segmenting the body into small volumes and summing them:
| $ I =\displaystyle\int_V r ^2 \rho dV $ |
resulting in
| $ I_{CM} =\displaystyle\frac{1}{2} m r_c ^2$ |
.
(ID 4434)
The moment of inertia of a cylinder rotating around a perpendicular ($\perp$) axis passing through the center is obtained by segmenting the body into small volumes and summing them:
| $ I =\displaystyle\int_V r ^2 \rho dV $ |
resulting in
| $ I_{CM} =\displaystyle\frac{1}{12} m ( h ^2+3 r_c ^2)$ |
.
(ID 4435)
The moment of inertia of a sphere rotating around an axis passing through its center is obtained by segmenting the body into small volumes and summing:
| $ I =\displaystyle\int_V r ^2 \rho dV $ |
resulting in
| $ I_{CM} =\displaystyle\frac{2}{5} m r_e ^2$ |
.
(ID 4436)
Examples
(ID 15604)
A bar with mass $m$ and length $l$ rotating around its center, which coincides with the center of mass:

(ID 10962)
A rotation of a cylinder with mass $m$ and radius $r$ around the axis of the cylinder, where the center of mass (CM) is located at mid-height:

(ID 10964)
In this scenario, a cylinder with mass $m$, radius $r$, and height $h$ is rotating around an axis perpendicular to its own axis. This axis passes through the midpoint of the cylinder's length, where the center of mass (CM) is located:

(ID 10965)
A sphere with mass $m$ and radius $r$ is rotating around its center of mass, which is located at its geometric center:

(ID 10490)
A straight rectangular parallelepiped with mass $m$ and sides $a$ and $b$, perpendicular to the axis of rotation, is rotating around its center of mass, which is located at the geometric center of the body:

(ID 10973)
In the case of a right rectangular parallelepiped with mass $m$ and side $a$, the center of mass is located at the geometric center:

(ID 10963)
(ID 15606)
ID:(1417, 0)
