Druyd:Knowledge

Dinámica de deslizamientos

Storyboard

Si se determina que una ladera tiene el potencial de experimentar un deslizamiento, es fundamental estudiar cómo podría ocurrir esto para comprender los riesgos involucrados. De esta manera, se pueden tomar medidas preventivas para minimizar al máximo los posibles daños indirectos provocados por el deslizamiento.

>Modelo

ID:(384, 0)

Estabilidad

Definición

Si analizamos las fuerzas sobre un terraplén notaremos que se puede dar una situación en que una parte del suelo esta expuesto a fuerzas tales que no logra la adhesión necesaria al resto del suelo precipitándose. De darse una situación de este tipo hablamos de que el terraplén es inestable.

Para comprender cuando se da esta situación se debe modelar un terraplén y mostrar que cualquier elemento que consideremos esta sujeto a fuerzas en que el roce asegura que no se desplace.

ID:(1135, 0)

Deslizamiento

Imagen

Si en alguna parte del sistema el peso que jala de las secciones superiores supera a las fuerzas de cohesión el suelo sufrirá un agrietamiento y el material inferior se deslizara hacia el valle:

Caso largo

ID:(7987, 0)

Zonas de inestabilidad

Nota

En general el peligro de desizamiento se incrementa por

- construcción de caminos
- desforestación
- fallas tectonicas
- los cimientos locales son debiles
- pendiente del terreno

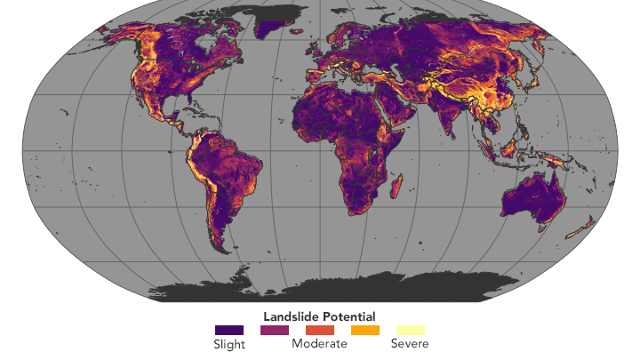
Con ello se logra desarrollar un mapa de peligro de deslizamiento:

ID:(9274, 0)

Dinámica de deslizamientos

Storyboard

Variables

Símbolo

Texto

Variable

Valor

Unidades

Calcule

Valor MKS

Unidades MKS

$H$

Altura de la capa

$h$

Altura de la columna

$w_c$

w_c

Altura de una plaquita de arcilla

$\theta$

theta

Ángulo de pendiente de la ladera

$\mu$

Coeficiente de roce

$\rho_b$

rho_b

Densidad aparente seca

kg/m^3

$\rho_w$

rho_w

Densidad del agua

kg/m^3

$\rho_s$

rho_s

Densidad sólida

kg/m^3

$V$

Energía potencial gravitacional

$g_a$

g_a

Fracción de masa de arena en la muestra

$F_c$

F_c

Fuerza de cohesión

$F_r$

F_r

Fuerza de roce

$F_t$

F_t

Fuerza de tracción en el plano

$F_s$

F_s

Fuerza paralelo al plano

$f_c$

f_c

Fuerza por grano

$L$

Largo

$L$

Largo de corte

$L$

Largo de la capa de suelo

$l_c$

l_c

Largo y ancho de una plaquita de arcilla

$M_w$

M_w

Masa de agua en el suelo

$M_g$

M_g

Masa del gas en el suelo

$f$

Porosidad

$D$

Rango de flujo

Cálculos

Ecuación

Número

Primero, seleccione la ecuación:

, luego, seleccione la variable:

Símbolo

Ecuación

Resuelto

Traducido

Cálculos

Símbolo

Ecuación

Resuelto

Traducido

Variable

Dado

Calcule

Objetivo :

Ecuación

A utilizar

Ecuaciones

$ F_s = F_t - F_r - F_c $

F_s = F_t - F_r - F_c

$ F_t =((1- f ) \rho_s H + f \rho_w h \cos \theta ) g L \Delta \sin \theta $

F_t =((1- f )* rho_s * H + f * rho_w * h *cos( theta )* g * L * Delta * sin( theta )

$ D =\displaystyle\frac{ L \sin \theta }{2 \mu \left(1-\displaystyle\frac{(1- f ) M_w }{ f ( M_s + M_w )}\right)}$

D =( L *sin( theta ))/(2* mu *(1-(1- f )* M_w /( f *( M_s + M_w ))))

$ F_t - F_r - F_c =0$

F_t - F_r - F_c =0

$L_c=\displaystyle\frac{\rho_bf_kf_m}{g\rho_sl_cw_c}\displaystyle\frac{(H-h\cos\theta)}{((1-f)\rho_sH+f\rho_wh\cos\theta)(\sin\theta-\mu\cos\theta)-(1-f)\rho_wh}$

L=(rho_b*f_k*f_m/(grho_s*l_c*w_c))*(H-h*cos(theta))/(((1-f)*H*rho_s+f*h*cos(theta)*rho_w)*(sin(theta)-mu*cos(theta))-(1-f)*h*rho_w))

$ F_r = \mu (((1- f ) \rho_s H + f \rho_w h \cos \theta ) \cos \theta - (1- f ) \rho_w h ) g L \Delta $

F_r = mu *(((1- f )* rho_s * H + f * rho_w 3 h *cos( theta )* cos( theta ) - (1- f )* rho_w * h )* g * L * Delta

$ F_c =\displaystyle\frac{ \rho_b f_m f_k }{ \rho_s l_c w_c }( H - h \cos \theta ) \Delta $

F_c = rho_p * f_m * f_k *( H - h *cos( theta )) * Delta /( rho_s * l_c * w_c )

$ V =( M_s + M_w ) g \displaystyle\frac{1}{2} L sin \theta $

V =( M_s + M_w )* g * L * sin( theta )/2

$V=\displaystyle\frac{1}{2}((1-f)\rho_sH+f\rho_wh\cos\theta) g L sin\theta$

V =((1- f )* rho_s * H + f * rho_w * h * cos( theta ) * g * L *sin(theta ))/2

Ejemplos

Estabilidad

Si analizamos las fuerzas sobre un terrapl n notaremos que se puede dar una situaci n en que una parte del suelo esta expuesto a fuerzas tales que no logra la adhesi n necesaria al resto del suelo precipit ndose. De darse una situaci n de este tipo hablamos de que el terrapl n es inestable.

Para comprender cuando se da esta situaci n se debe modelar un terrapl n y mostrar que cualquier elemento que consideremos esta sujeto a fuerzas en que el roce asegura que no se desplace.

Fuerza de tracci n con geometr a

Las fuerza de tracci n

equation=4493

se puede rescribir con la masa solida

equation=4489

y la masa de agua

equation=4492

de la forma

kyon

Fuerza de roce con geometr a

Las fuerza de tracci n

equation=4494

se puede rescribir con la masa solida

equation=4489

y la masa de agua

equation=4492

ademas de la fuerza hidrostatica

equation=4495

por lo que queda de la forma

kyon

Fuerza de cohesi n con geometr a

Para simplificar la notaci n de la fuerza de cohesi n

equation=4490

la expresi n para el numero de enlaces

equation=2973

y la seccion no saturada

equation=2975

se obtiene

kyon

Energ a potencial gravitacional con geometr a

La energ a potencial gravitacional se calcula de la masa y altura del cuerpo

equation=4501

en que se tienen que tomar las masas del suelo

equation=4489

y del agua

equation=4492

La altura del centro de masa corresponde al cateto opuesto de un triangulo donde el angulo es la inclinaci n y la hipotenusa la mitad del largo de corte L/2. Con ello la energ a potencial gravitacional se calcula de

kyon

Energ a potencial gravitacional de la capa

La energ a potencial gravitacional se calcula de la masa y altura del cuerpo

equation=3245

en que se tienen que tomar las masas del suelo M_s y la masa del agua M_w. Por otro lado la altura del centro de masa corresponde al cateto opuesto de un triangulo donde el angulo es la inclinaci n y la hipotenusa la mitad del largo de corte L/2. Con ello la energ a potencial gravitacional se calcula de

kyon

Fuerzas en el plano

La fuerza total que act a en el plano es la fuerza de tracci n gravitacional

equation=4493

menos la fuerza de roce

equation=4494

y menos la fuerza de cohesi n

equation=4490

lo que resulta en una fuerza total de

kyon

Limite de inestabilidad

El sistema se vuelve inestable al momento de que la fuerza total

equation=20

se vuelve nula

kyon

Deslizamiento

Si en alguna parte del sistema el peso que jala de las secciones superiores supera a las fuerzas de cohesi n el suelo sufrir un agrietamiento y el material inferior se deslizara hacia el valle:

image

Largo de corte

Si se observan las fuerzas de tracci n

equation=3163

y roce

equation=4499

con con la fuerza de cohesi n

equation=4500

se tiene la condici n de inestabilidad

equation=4496

define los largos L mediante

kyon

El cerro es por ello estable si el largo de corte es mas largo que la ladera hasta la parte mas alta.

Rango de flujo

Como la energ a potencial

equation=4501

se transforma en cin tica y esta a su vez via el roce en calor se puede estimar la distancia recorrida considerando que la energ a disipada es igual a la fuerza de roce por el camino recorrido.

Si se asume que la mayor disipaci n ocurre en el valle sin inclinaci n la fuerza de roce se puede considerar con

equation=4494

y

equation=4495

bajo un angulo de inclinaci n nula. De esta forma el camino recorrido ser a.

kyon

Zonas de inestabilidad

En general el peligro de desizamiento se incrementa por

- construcci n de caminos
- desforestaci n
- fallas tectonicas
- los cimientos locales son debiles
- pendiente del terreno

Con ello se logra desarrollar un mapa de peligro de deslizamiento:

image

>Modelo

ID:(384, 0)