Condición de Desplazamiento
Storyboard 
Se estudia las condiciones bajo las cuales un cuerpo que se adhiere a un plano por el efecto del rose puede comenzar a deslizarse.
ID:(382, 0)
Ejemplo de deslizamiento
Definición 
En condiciones de lluvias extremas se observan deslizamientos de suelo que pueden comprometer poblados y vías publicas:

Desplazamiento de Tierra
Para comprender la dinámica y la perdida de estabilidad procederemos a construir un modelo simple de una capa de suelo sobre un suelo rocoso sobre el que se puede deslizar. La clave esta en comprender la dinámica del roce y las fuerzas en torno de el.
ID:(2357, 0)
Esquema del deslizamiento
Imagen 
Cuando el terreno cede crea un área en que el material sede y fluye fuera de su zona original mientras la parte superior se hunde:
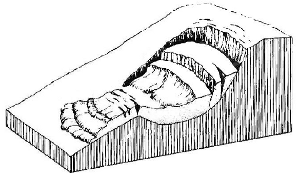
Desplazamiento de una sección
ID:(2358, 0)
Mecanismos de desplazamiento
Nota 
Existen distintos mecanismos de desplazamiento dependiendo de la geometría y tipo de suelo/roca. En general ocurre en alguna parte un corte y el desprendimiento de la masa debajo de este:

Estabilidad del suelo
ID:(2359, 0)
Condición de desplazamiento
Cita 
El cuerpo comenzara a deslizarse si en algún momento la fuerza de tracción
ID:(1133, 0)
Fuerzas normal y de roce
Ejercicio 
La fuerza normal
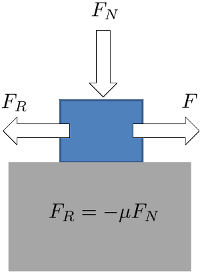
Coeficiente de roce
ID:(1640, 0)
Plano inclinado
Ecuación 
En el caso del suelo la situación asemeja a un plano inclinado sobre el cual se desliza una sección del terreno. Por ello debemos primero analizar como se comporta un sistema de este tipo, en partícula respecto de las fuerzas normales y de tracción que surgen por efecto de la gravedad:
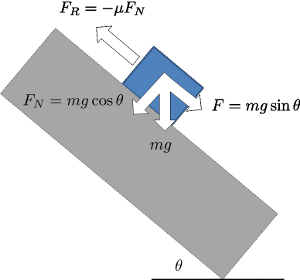
Sección de suelo
ID:(2360, 0)
Condición de Desplazamiento
Storyboard 
Se estudia las condiciones bajo las cuales un cuerpo que se adhiere a un plano por el efecto del rose puede comenzar a deslizarse.
Variables
Cálculos
Cálculos
Ecuaciones
Ejemplos
En condiciones de lluvias extremas se observan deslizamientos de suelo que pueden comprometer poblados y v as publicas:
Para comprender la din mica y la perdida de estabilidad procederemos a construir un modelo simple de una capa de suelo sobre un suelo rocoso sobre el que se puede deslizar. La clave esta en comprender la din mica del roce y las fuerzas en torno de el.
Cuando el terreno cede crea un rea en que el material sede y fluye fuera de su zona original mientras la parte superior se hunde:
Existen distintos mecanismos de desplazamiento dependiendo de la geometr a y tipo de suelo/roca. En general ocurre en alguna parte un corte y el desprendimiento de la masa debajo de este:
El cuerpo comenzara a deslizarse si en alg n momento la fuerza de tracci n
La fuerza normal
El roce
El desplazamiento se inicia si en alg n momento la fuerza de tracci n vence a la de roce:
En el caso del suelo la situaci n asemeja a un plano inclinado sobre el cual se desliza una secci n del terreno. Por ello debemos primero analizar como se comporta un sistema de este tipo, en part cula respecto de las fuerzas normales y de tracci n que surgen por efecto de la gravedad:
La fuerza gravitacional es igual a la masa por la aceleraci n gravitacional:
En un plano inclinado la fuerza de tracci n es generada por la propia masa a trav s de la componente de la fuerza paralela al plano de deslizamiento. Si el angulo del plano es
En un plano inclinado la fuerza normal es generada por la propia masa a trav s de la componente de la fuerza perpendicular al plano de deslizamiento. Si el angulo del plano es
Como el cuerpo comenzara a deslizarse si la fuerza de tracci n
y esta ultima es igual al coeficiente de roce
$F_T>\mu F_N$
Si por otro lado el objeto est n en el plano inclinado con un angulo
y la normal
$Mg\sin\alpha_c=\mu Mg\cos\alpha$
por lo que
ID:(382, 0)
