Utilisateur:
Mécanisme de conduction thermique
Image 
Pour comprendre comment la chaleur est conduite, vous pouvez imaginer qu'un corps peut être représenté par des chaînes de ressorts qui oscillent en fonction de leur température. Si une extrémité du corps a une température plus élevée, l'oscillation correspondante sera également plus grande. À mesure que l'on s'éloigne de cette extrémité, les ressorts voisins oscillent avec une amplitude moindre, ce qui entraîne une distribution progressive de l'oscillation/température le long de la chaîne, comme illustré ci-dessous :
La capacité de conduction de la chaleur sera d'autant plus élevée qu'il y aura plus de chaînes (section transversale) présentes, et elle sera plus lente à mesure que les chaînes deviendront plus longues.
ID:(11188, 0)
Mécanismes de transport de chaleur
Modèle
Variables
Calculs
à 
,
puis, sélectionnez la variable: 
à 
Calculs
Variable
Donnée
Calculer
Cible :
Équation
À utiliser
Équations
tant donn que a chaleur transportée ($dQ$) est une fonction de le longueur du pilote ($L$), a section ($S$), a variation temporelle ($dt$), a différence de température dans le conducteur ($\Delta T_0$) et a conductivité thermique ($\lambda$) selon l' quation suivante :
| $ q = \displaystyle\frac{ \lambda }{ L } \Delta T_0 $ |
Avec l' quation pour a débit de chaleur ($q$) d finie comme suit :
| $ q \equiv \displaystyle\frac{1}{ S }\displaystyle\frac{ dQ }{ dt }$ |
Dans le cas infinit simal, o le longueur du pilote ($L$) se r duit une distance parcourue ($dz$) et a différence de température dans le conducteur ($\Delta T_0$) devient a variation de température ($dT$), l' quation se simplifie :
| $ q = - \lambda \displaystyle\frac{dT}{dz}$ |
(ID 15132)
La quantit de a chaleur transportée ($dQ$) travers une distance parcourue ($dz$) peut tre calcul e en utilisant a débit de chaleur ($q$) et a variation temporelle ($dt$) avec a section ($S$) gr ce l' quation suivante :
$dQ = -\displaystyle\frac{\partial}{\partial z}(q S dt) dz$
Puisque a débit de chaleur ($q$) avec a variation de température ($dT$) et a conductivité thermique ($\lambda$) est d fini comme suit :
| $ q = - \lambda \displaystyle\frac{dT}{dz}$ |
Par cons quent,
$dQ = \displaystyle\frac{\partial}{\partial z}(\lambda \displaystyle\frac{\partial T}{\partial z}) S dz dt$
D'autre part, nous pouvons relier a chaleur fournie au liquide ou au solide ($\Delta Q$) avec a masse ($M$), le chaleur spécifique ($c$) et a variation de température ($\Delta T$) gr ce l' quation suivante :
| $ \Delta Q = M c \Delta T$ |
Dans ce cas, avec a variation de volume ($\Delta V$), l' quation devient :
$dQ=\rho dV c dT = \rho c S dz dT$
Et enfin, nous obtenons :
| $ \displaystyle\frac{\partial T}{\partial t}=\displaystyle\frac{\lambda}{\rho c}\displaystyle\frac{\partial^2 T}{\partial z^2}$ |
(ID 15134)
Exemples
(ID 15274)
Dans le cas d'un solide, et de mani re similaire pour un liquide, nous pouvons d crire le syst me comme une structure d'atomes li s par quelque chose qui se comporte comme un ressort. Lorsque les deux extr mit s ont des temp ratures de une différence de température dans le conducteur ($\Delta T_0$), avec a température de la surface intérieure ($T_{is}$) et a température de la surface extérieure ($T_{es}$) :
| $ \Delta T_0 = T_{is} - T_{es} $ |
La diff rence de temp rature implique que les atomes aux extr mit s oscillent de mani re diff rente ; les atomes dans la zone haute temp rature auront une amplitude plus grande dans leurs oscillations par rapport aux atomes dans la zone basse temp rature.
Cependant, cette diff rence conduira progressivement ce que toute la cha ne oscille de telle mani re qu' la fin, l'amplitude variera le long du chemin, depuis les valeurs les plus lev es l o la temp rature est galement plus lev e, jusqu'aux valeurs les plus basses dans la zone basse temp rature.
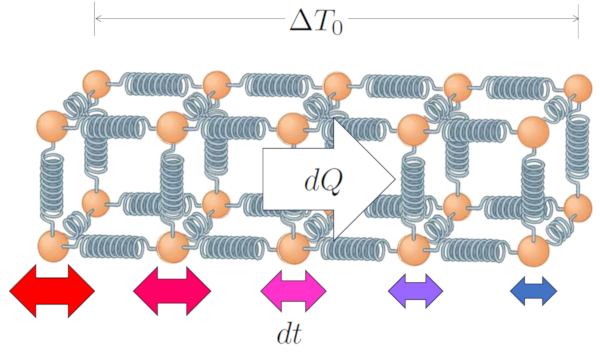
De cette mani re, a différence de température dans le conducteur ($\Delta T_0$) m ne une chaleur transportée ($dQ$) en une variation temporelle ($dt$).
(ID 15234)
Pour comprendre comment la chaleur est conduite, vous pouvez imaginer qu'un corps peut tre repr sent par des cha nes de ressorts qui oscillent en fonction de leur temp rature. Si une extr mit du corps a une temp rature plus lev e, l'oscillation correspondante sera galement plus grande. mesure que l'on s' loigne de cette extr mit , les ressorts voisins oscillent avec une amplitude moindre, ce qui entra ne une distribution progressive de l'oscillation/temp rature le long de la cha ne, comme illustr ci-dessous :
La capacit de conduction de la chaleur sera d'autant plus lev e qu'il y aura plus de cha nes (section transversale) pr sentes, et elle sera plus lente mesure que les cha nes deviendront plus longues.
(ID 11188)
Les mod les de transfert de chaleur et de conduction sugg rent qu'il est possible de d velopper une relation qui int gre ces trois m canismes ensemble. Cette quation devrait prendre en compte a chaleur transportée ($dQ$), a variation temporelle ($dt$), a différence de température ($\Delta T$), a section ($S$) et le coefficient de transport total (supports multiples, deux interfaces) ($k$) :
Math matiquement, cela peut s'exprimer comme suit :
| $ q = k \Delta T $ |
(ID 15241)
L'un des effets du transfert de chaleur d'un conducteur un milieu externe est le r chauffement du milieu pr s de l'interface, cr ant une zone d'interf rence dans la transmission. Cela diminue l'efficacit du transfert et tend former une couche isolante qui r duit le flux d' nergie.
Cependant, cet effet peut changer en pr sence de vent. Le vent peut liminer la couche d'atomes et de mol cules haute temp rature, am liorant ainsi l'efficacit du transfert de chaleur. Cela sugg re que le coefficient de transmission ($\alpha$) est influenc par a vitesse moyenne ($v_m$) [1,2] :
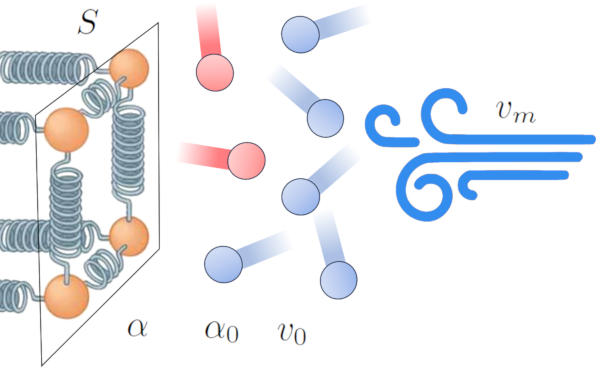
Dans ce contexte, nous mod lisons la relation en fonction de ERROR:9844,0 et d'un facteur de r f rence de le vitesse de référence du support ($v_0$).
La relation math matique qui d crit ce ph nom ne pour un gaz avec le coefficient de transmission dans les gaz, en fonction de la vitesse ($\alpha_{gv}$), a vitesse moyenne ($v_m$), le coefficient de transmission dans les gaz, indépendant de la vitesse ($\alpha_{g0}$) et le coefficient de transmission Facteur de vitesse du gaz ($v_{g0}$) est :
| $ \alpha_{gv} = \alpha_{g0} \left(1+\displaystyle\frac{ v_m }{ v_{g0} }\right)$ |
Et pour un liquide avec le coefficient de transmission dans le liquide, en fonction de la vitesse ($\alpha_{wv}$), a vitesse moyenne ($v_m$), le coefficient de transmission dans le liquide, indépendant de la vitesse ($\alpha_{w0}$) et le coefficient de transmission Facteur de vitesse du liquide ($v_{w0}$) :
| $ \alpha_{wv} = \alpha_{w0} \left(1+\sqrt{\displaystyle\frac{ v_m }{ v_{w0} }}\right)$ |
Cela illustre comment le vent peut influencer de mani re significative l'efficacit du transfert de chaleur entre un conducteur et un milieu externe.
[1] " ber Fl ssigkeitsbewegung bei sehr kleiner Reibung" (Sur le mouvement des fluides avec tr s peu de friction), Ludwig Prandtl, 1904 [2] "Die Abh ngigkeit der W rme bergangszahl von der Rohrl nge" (La d pendance du coefficient de transfert de chaleur la longueur du tuyau), Wilhelm Nusselt, 1910
(ID 3620)
(ID 15333)
ID:(1512, 0)