Usuario:
Mecanismo de conducción del Calor
Imagen 
Para comprender cómo se conduce el calor, podemos imaginar que un cuerpo se puede representar como cadenas de resortes que oscilan en respuesta a su temperatura. Si en un extremo del cuerpo la temperatura es más alta, la oscilación correspondiente será más intensa. A medida que nos alejamos de ese extremo, los resortes vecinos oscilan con menor amplitud, lo que resulta en una distribución gradual de la oscilación/temperatura a lo largo de la cadena, como se ilustra a continuación:
Conducción
La capacidad de conducción de calor será mayor cuanto más numerosas sean las cadenas (sección) presentes y será más lenta a medida que las cadenas sean más largas.
ID:(11188, 0)
Mecanismos de transporte de calor
Modelo
Variables
Cálculos
a 
,
luego, seleccione la variable: 
a 
Cálculos
Variable
Dado
Calcule
Objetivo :
Ecuación
A utilizar
Ecuaciones
Dado que la calor transportado ($dQ$) se expresa como una funci n de el largo del conductor ($L$), la sección ($S$), la variación de tiempo ($dt$), la diferencia de temperatura en el conductor ($\Delta T_0$) y la conductividad térmica ($\lambda$) mediante la siguiente ecuaci n:
| $ q = \displaystyle\frac{ \lambda }{ L } \Delta T_0 $ |
Con la ecuaci n para la tasa de flujo de calor ($q$) definida como:
| $ q \equiv \displaystyle\frac{1}{ S }\displaystyle\frac{ dQ }{ dt }$ |
En el caso infinitesimal, donde el largo del conductor ($L$) se reduce a una distancia recorrida ($dz$) y la diferencia de temperatura en el conductor ($\Delta T_0$) se convierte en la variación de la temperatura ($dT$), la ecuaci n se simplifica a:
| $ q = - \lambda \displaystyle\frac{dT}{dz}$ |
(ID 15132)
La cantidad de la calor transportado ($dQ$) a trav s de una distancia recorrida ($dz$) puede calcularse utilizando la tasa de flujo de calor ($q$) y la variación de tiempo ($dt$) con la sección ($S$) mediante la siguiente ecuaci n:
$dQ = -\displaystyle\frac{\partial}{\partial z}(q S dt) dz$
Dado que la tasa de flujo de calor ($q$) con la variación de la temperatura ($dT$) y la conductividad térmica ($\lambda$), obtenemos:
| $ q = - \lambda \displaystyle\frac{dT}{dz}$ |
Por lo tanto,
$dQ = \displaystyle\frac{\partial}{\partial z}(\lambda \displaystyle\frac{\partial T}{\partial z}) S dz dt$
Por otro lado, podemos relacionar la calor suministrado al liquido o solido ($\Delta Q$) con la masa ($M$), el calor específico ($c$) y la variación de la temperatura ($\Delta T$) mediante la ecuaci n:
| $ \Delta Q = M c \Delta T$ |
En este caso, con la variación del volumen ($\Delta V$), la ecuaci n se convierte en:
$dQ=\rho dV c dT = \rho c S dz dT$
Finalmente, obtenemos:
| $ \displaystyle\frac{\partial T}{\partial t}=\displaystyle\frac{\lambda}{\rho c}\displaystyle\frac{\partial^2 T}{\partial z^2}$ |
(ID 15134)
Ejemplos
(ID 15274)
En el caso de un s lido, y de manera similar para un l quido, podemos describir el sistema como una estructura de tomos unidos por algo que se comporta como un resorte. Cuando ambos extremos tienen valores de temperatura de una diferencia de temperatura en el conductor ($\Delta T_0$), siendo la temperatura en la superficie interior ($T_{is}$) y la temperatura en la superficie exterior ($T_{es}$):
| $ \Delta T_0 = T_{is} - T_{es} $ |
La diferencia en temperaturas implica que los tomos en los extremos oscilan de manera distinta; los tomos en la zona de alta temperatura tendr n una amplitud mayor en sus oscilaciones en comparaci n con los tomos en la zona de baja temperatura.
Sin embargo, esta diferencia llevar gradualmente a que toda la cadena oscile de tal manera que, al final, la amplitud variar a lo largo del camino, desde los valores m s altos donde la temperatura tambi n es mayor, hasta los valores m s bajos en la zona de menor temperatura.
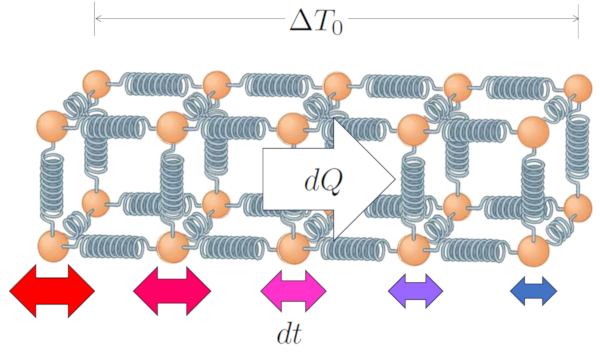
De esta manera, la diferencia de temperatura en el conductor ($\Delta T_0$) conduce a una calor transportado ($dQ$) en una variación de tiempo ($dt$).
(ID 15234)
Para comprender c mo se conduce el calor, podemos imaginar que un cuerpo se puede representar como cadenas de resortes que oscilan en respuesta a su temperatura. Si en un extremo del cuerpo la temperatura es m s alta, la oscilaci n correspondiente ser m s intensa. A medida que nos alejamos de ese extremo, los resortes vecinos oscilan con menor amplitud, lo que resulta en una distribuci n gradual de la oscilaci n/temperatura a lo largo de la cadena, como se ilustra a continuaci n:
Conducci n
La capacidad de conducci n de calor ser mayor cuanto m s numerosas sean las cadenas (secci n) presentes y ser m s lenta a medida que las cadenas sean m s largas.
(ID 11188)
Los modelos de transferencia y conducci n de calor sugieren que es posible desarrollar una relaci n que incorpore los tres mecanismos en conjunto. Esta ecuaci n deber tener en cuenta la calor transportado ($dQ$), la variación de tiempo ($dt$), la diferencia de temperatura ($\Delta T$), la sección ($S$) y el coeficiente de total de transporte (multiple medio, dos interfaces) ($k$):
Matem ticamente, esto se puede expresar de la siguiente manera:
| $ q = k \Delta T $ |
(ID 15241)
Uno de los efectos de la transferencia de calor de un conductor a un medio externo es el calentamiento del medio cercano a la interfaz, creando una zona de interferencia en la transmisi n. Esto disminuye la eficiencia de la transferencia y tiende a formar una capa aislante que reduce el flujo de energ a.
Sin embargo, este efecto puede modificarse en presencia de viento. El viento puede disipar la capa de tomos y mol culas a alta temperatura, aumentando la eficiencia de la transferencia de calor. Esto indica que el coeficiente de transmisión ($\alpha$) est influenciado por la velocidad del medio ($v_m$) [1,2]:
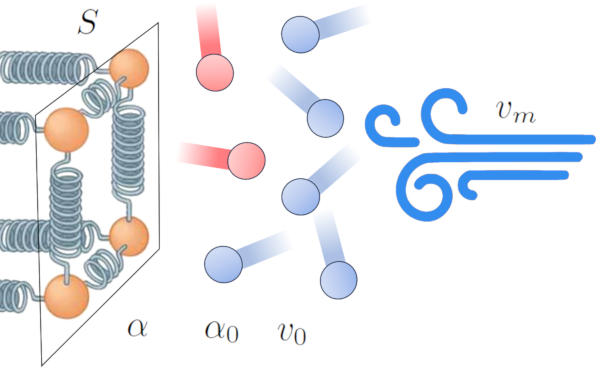
En este contexto, modelamos la relaci n en funci n de ERROR:9844,0 y un factor de referencia el velocidad de referencia del medio ($v_0$).
La relaci n matem tica que describe este fen meno para un gas con el coeficiente de transmisión en gases, dependiente de la velocidad ($\alpha_{gv}$), la velocidad del medio ($v_m$), el coeficiente de transmisión en gases, independiente de la velocidad ($\alpha_{g0}$) y el factor velocidad del gas del coeficiente de transmisión ($v_{g0}$) es:
| $ \alpha_{gv} = \alpha_{g0} \left(1+\displaystyle\frac{ v_m }{ v_{g0} }\right)$ |
Y para un l quido con el coeficiente de transmisión en liquido, dependiente de la velocidad ($\alpha_{wv}$), la velocidad del medio ($v_m$), el coeficiente de transmisión en liquido, independiente de la velocidad ($\alpha_{w0}$) y el factor velocidad del liquido del coeficiente de transmisión ($v_{w0}$):
| $ \alpha_{wv} = \alpha_{w0} \left(1+\sqrt{\displaystyle\frac{ v_m }{ v_{w0} }}\right)$ |
Esto demuestra c mo el viento puede afectar significativamente la eficiencia de la transferencia de calor entre un conductor y un medio externo.
[1] " ber Fl ssigkeitsbewegung bei sehr kleiner Reibung" (Sobre el movimiento de fluidos con muy poca fricci n), Ludwig Prandtl, 1904 [2] "Die Abh ngigkeit der W rme bergangszahl von der Rohrl nge" (La dependencia del coeficiente de transferencia de calor de la longitud del tubo), Wilhelm Nusselt, 1910
(ID 3620)
(ID 15333)
ID:(1512, 0)