Quiebre de olas
Storyboard 
La corriente de aire sobre el océano impulsa el movimiento en el agua, generando olas que, ante fluctuaciones, muestran un comportamiento distinto dependiendo de la profundidad. Este fenómeno es conocido como el quiebre de las olas. Este quiebre ocurre porque la velocidad de propagación de la ola es mayor en zonas de mayor profundidad. Así, al acercarse a la costa, las olas provenientes de áreas más profundas tienden a sobrepasar a las de zonas menos profundas, generando el típico quiebre de la ola.
ID:(1632, 0)
Quiebre de la ola en la playa
Descripción 
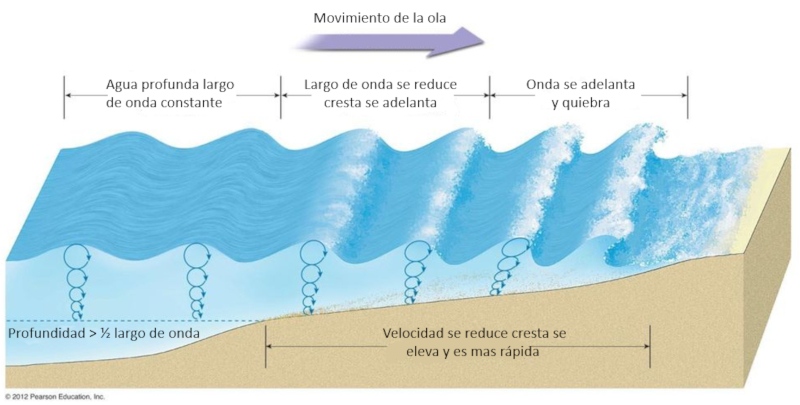
Cuando una ola alcanza la playa, comienza a elevarse mientras se desplaza hacia arriba de la pendiente de la playa, volviéndose cada vez más superficial y, por lo tanto, más lenta. Una segunda ola que le sigue tiende a elevarse sobre la ola anterior. Debido a que el agua se vuelve más profunda en esta situación, la segunda ola es más rápida y tiende a sobrepasar a la ola que llegó primero a la playa. Esta interacción entre las olas provoca la ruptura de las olas, creando el fenómeno conocido como rompiente.
ID:(12308, 0)
Frecuencia angular
Concepto 
Recordando que la velocidad angular representa el ángulo recorrido por unidad de tiempo, se puede observar que la expresión
$\displaystyle\frac{2\pi}{T}$
corresponde a una vuelta completa ($2\pi$) dividida por el tiempo la período ($T$), necesario para completar un ciclo. Por esta razón, se define la frecuencia angular ($\omega$) como
| $ \omega = \displaystyle\frac{2 \pi }{ T }$ |
ID:(15648, 0)
Vector de onda
Concepto 
El vector de onda ($k$) es el factor que multiplica la posición y corresponde al valor para el cual, si la onda se desplaza a lo largo de un largo de onda ($\lambda$), retoma la misma forma que tenía inicialmente. Para que esto ocurra, se debe cumplir que:
$kx = k\lambda = 2\pi$
Por lo tanto, con el largo de onda ($\lambda$), establecemos que:
| $ k =\displaystyle\frac{2 \pi }{ \lambda }$ |
ID:(15647, 0)
Velocidad de fase de las olas
Concepto 
La velocidad de las olas depende de la profundidad del agua y del factor el vector de onda ($k$), que se calcula usando el largo de onda ($\lambda$) de la siguiente manera:
| $ k =\displaystyle\frac{2 \pi }{ \lambda }$ |
En relación con el velocidad de fase ($c_p$), que corresponde a la velocidad a la que se desplaza cada cresta de la ola, esta se puede determinar utilizando el profundidad del océano ($h$) y la aceleración gravitacional ($g$). El velocidad de fase ($c_p$) se calcula como:
| $ c_p =\sqrt{\displaystyle\frac{ g }{ k } \tanh( k h )}$ |
La velocidad de fase, en este contexto, se refiere a la velocidad a la que se desplaza una oscilación o una onda específica.
ID:(15649, 0)
Velocidad de grupo de las olas
Concepto 
Las olas tienen una velocidad que depende de la profundidad del agua y del factor el vector de onda ($k$), calculado usando el largo de onda ($\lambda$) de la siguiente manera:
| $ k =\displaystyle\frac{2 \pi }{ \lambda }$ |
Para el velocidad de grupo ($c_g$), que representa la velocidad a la que se mueve el conjunto del tren de olas y no cada ola individualmente, se puede calcular utilizando el velocidad de fase ($c_p$). Esta última se determina con el profundidad del océano ($h$) y la aceleración gravitacional ($g$), de la siguiente forma:
| $ c_p =\sqrt{\displaystyle\frac{ g }{ k } \tanh( k h )}$ |
Finalmente, utilizando esta información, se puede calcular el velocidad de grupo ($c_g$) mediante la siguiente expresión:
| $ c_g =\displaystyle\frac{ c_p }{2}\left(1 + \displaystyle\frac{2 k h }{\sinh(2 k h )}\right)$ |
La velocidad de grupo es la velocidad a la que el tren o grupo de olas se desplaza en el medio acuático.
ID:(15650, 0)
Velocidades de ondas
Imagen 
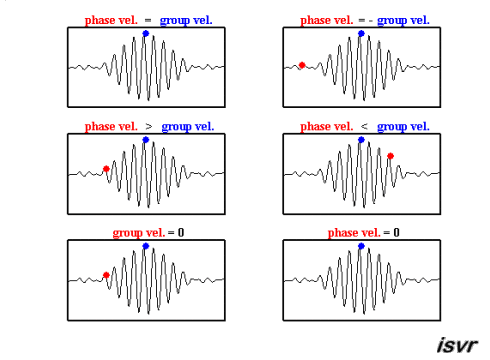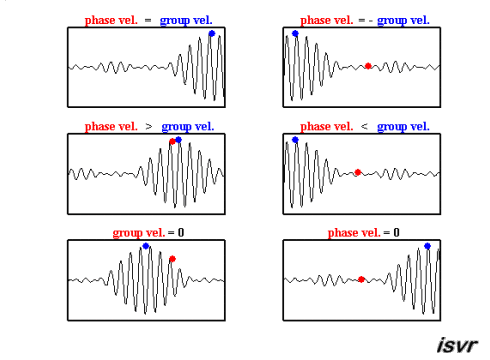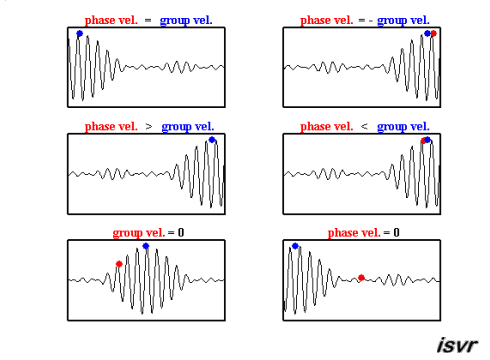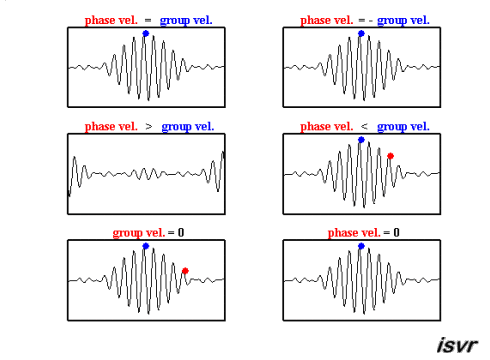
Existen dos velocidades características en la mecánica de ondas. Por un lado, está la velocidad con la que se desplaza una onda específica, que puede variar según la frecuencia, diferenciándose así de una onda a otra.
El segundo tipo de velocidad es la de un paquete de ondas, es decir, un conjunto de ondas de diferentes frecuencias y fases que, al superponerse, forman un grupo que se mueve como una unidad. Esta velocidad es conocida como velocidad de grupo.
Ambas velocidades se pueden observar en esta animación:
ID:(15651, 0)
Descripción de la ola
Concepto 
Una ola se puede describir aproximadamente como una función sinusoidal dependiendo de las variables el posición ($x$) y el tiempo ($t$).
La función considera los valores de el altura de la ola ($u$) en cada punto, así como el altura máxima de la ola ($z_0$), el vector de onda ($k$), y el frecuencia angular ($\omega$):
| $ u( x , t ) = z_0 \cos( k x - \omega t )$ |
ID:(15646, 0)
Quiebre de olas
Modelo 
La corriente de aire sobre el océano impulsa el movimiento en el agua, generando olas que, ante fluctuaciones, muestran un comportamiento distinto dependiendo de la profundidad. Este fenómeno es conocido como el quiebre de las olas. Este quiebre ocurre porque la velocidad de propagación de la ola es mayor en zonas de mayor profundidad. Así, al acercarse a la costa, las olas provenientes de áreas más profundas tienden a sobrepasar a las de zonas menos profundas, generando el típico quiebre de la ola.
Variables
Cálculos
Cálculos
Ecuaciones
(ID 16208)
Ejemplos
(ID 15639)
Cuando una ola alcanza la playa, comienza a elevarse mientras avanza sobre la pendiente del litoral, volvi ndose progresivamente m s superficial y, por lo tanto, m s lenta. Una segunda ola que la sigue tiende a montarse sobre la anterior. Como en esa zona el agua es m s profunda, la segunda ola se desplaza m s r pidamente y tiende a alcanzar y sobrepasar a la primera. Esta interacci n entre olas genera la ruptura del frente de ola, dando lugar al fen meno conocido como rompiente.

Este fen meno puede modelarse mediante la descripci n de el altura de la ola ($u$) a trav s de una onda de el altura máxima de la ola ($z_0$) que se propaga con un el vector de onda ($k$) y el frecuencia angular ($\omega$), cuya expresi n en el posición ($x$) y el tiempo ($t$) es:
| $ u( x , t ) = z_0 \cos( k x - \omega t )$ |
El agua realiza un movimiento circular cuya velocidad cumple con las relaciones definidas por la velocidad de la ola ($v_{\omega}$) y el profundidad del océano ($h$):
| $ v_{\omega,x} = v_{\omega} \cosh( k ( z + h )) \cos( k x - \omega t )$ |
y
| $ v_{\omega,z} = v_{\omega} \sinh( k ( z + h )) \sin( k x - \omega t )$ |
(ID 12308)
Recordando que la velocidad angular representa el ngulo recorrido por unidad de tiempo, se puede observar que la expresi n
$\displaystyle\frac{2\pi}{T}$
corresponde a una vuelta completa ($2\pi$) dividida por el tiempo la período ($T$), necesario para completar un ciclo. Por esta raz n, se define la frecuencia angular ($\omega$) como
| $ \omega = \displaystyle\frac{2 \pi }{ T }$ |
(ID 15648)
El vector de onda ($k$) es el factor que multiplica la posici n y corresponde al valor para el cual, si la onda se desplaza a lo largo de un largo de onda ($\lambda$), retoma la misma forma que ten a inicialmente. Para que esto ocurra, se debe cumplir que:
$kx = k\lambda = 2\pi$
Por lo tanto, con el largo de onda ($\lambda$), establecemos que:
| $ k =\displaystyle\frac{2 \pi }{ \lambda }$ |
(ID 15647)
La velocidad de las olas depende de la profundidad del agua y del factor la frecuencia angular ($\omega$), que se determina a partir de el velocidad de fase ($c_p$) y el vector de onda ($k$) de la siguiente manera:
| $ \omega = c_p k $ |
En relaci n con el velocidad de fase ($c_p$), que representa la velocidad a la que se desplaza cada cresta de la ola, esta puede calcularse utilizando el profundidad del océano ($h$) y la aceleración gravitacional ($g$). El valor de el velocidad de fase ($c_p$) se obtiene mediante:
| $ c_p =\sqrt{\displaystyle\frac{ g }{ k } \tanh( k h )}$ |
En este contexto, la velocidad de fase se refiere a la velocidad con la que se propaga una oscilaci n o una onda individual.
(ID 15649)
Las olas tienen una velocidad que depende de la profundidad del agua y del factor el vector de onda ($k$), calculado usando el largo de onda ($\lambda$) de la siguiente manera:
| $ \omega = c_p k $ |
Para el velocidad de grupo ($c_g$), que representa la velocidad a la que se mueve el conjunto del tren de olas y no cada ola individualmente, se puede calcular utilizando el velocidad de fase ($c_p$). Esta ltima se determina con el profundidad del océano ($h$) y la aceleración gravitacional ($g$), de la siguiente forma:
| $ c_g = \displaystyle\frac{d \omega }{d k }$ |
Finalmente, utilizando esta informaci n, se puede calcular el velocidad de grupo ($c_g$) mediante la siguiente expresi n:
| $ c_g =\displaystyle\frac{ c_p }{2}\left(1 + \displaystyle\frac{2 k h }{\sinh(2 k h )}\right)$ |
La velocidad de grupo es la velocidad a la que el tren o grupo de olas se desplaza en el medio acu tico.
(ID 15650)
Existen dos velocidades caracter sticas en la mec nica de ondas. Por un lado, est la velocidad con la que se desplaza una onda espec fica, que puede variar seg n la frecuencia, diferenci ndose as de una onda a otra.
El segundo tipo de velocidad es la de un paquete de ondas, es decir, un conjunto de ondas de diferentes frecuencias y fases que, al superponerse, forman un grupo que se mueve como una unidad. Esta velocidad es conocida como velocidad de grupo.
Ambas velocidades se pueden observar en esta animaci n:

(ID 15651)
(ID 15644)
ID:(1632, 0)
