Modelo de superficie
Storyboard 
El intercambio de partículas o moléculas, como el CO2, entre la atmósfera y el océano implica un mecanismo más complejo. Este proceso está relacionado con la formación de una película de líquido saturado con partículas o moléculas, que regula el tránsito de nuevas partículas hacia o desde el interior del océano.
ID:(1633, 0)
Capa de superficie
Descripción 
Para estudiar la transferencia de CO2 en la superficie del océano, es necesario observar detalladamente lo que ocurre con las concentraciones tanto en el aire como en el agua.
En el aire, el CO2 ingresa al agua creando una zona de baja concentración en la que disminuye de $C_a$ a $C_{a,0}$. Esta capa tiene un grosor entre 0,1 y 1 mm.
El CO2 que ingresa al agua se acumula inicialmente en la superficie, creando una concentración $C_{w,0}$ que luego se difunde hacia el interior, alcanzando una concentración menor de $C_w$.
La reducción de concentración permite definir dos zonas: una muy delgada de solo 0,02 a 0,2 mm, donde la concentración disminuye rápidamente, y una segunda zona de 0,6 a 2 mm, donde la concentración disminuye de manera más suave hasta alcanzar la concentración en el interior del agua.
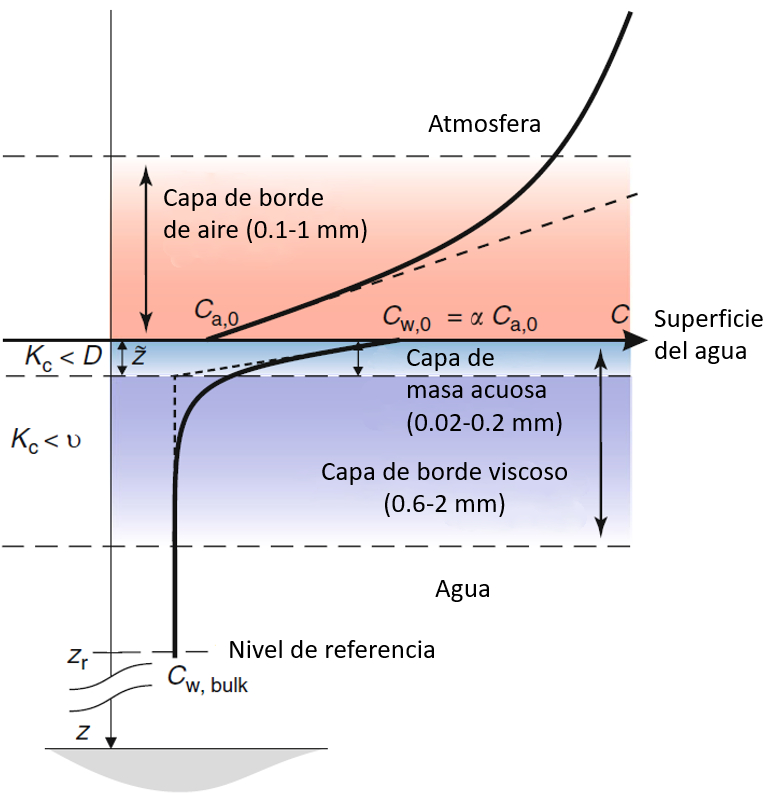
Ocean-Atmosphere Interactions of Gases and Particles, Peter S. Liss, Martin T. Johnson (eds.), Springer-Verlag Berlin Heidelberg
ID:(12244, 0)
Intercambio de CO2, velocidad desde el aire
Concepto 
La velocidad de transferencia del gas en el agua ($k_w$) puede ser modelada utilizando datos medidos. En primer lugar, depende de la velocidad a la cual el sistema remueve el carbono de la interfaz aire-agua, lo que hace que la velocidad de transporte sea proporcional a la velocidad relativa entre ambos medios.
En segundo lugar, se presenta un efecto de la movilidad de los iones, que puede describirse mediante el número de Schmidt ($Sc$), representando la relación entre la difusión del impulso y las partículas. Sin embargo, esta dependencia no es lineal y está influenciada por un factor ERROR:9926 que varía entre -1/2 y -2/3 según la rugosidad de la superficie.
Finalmente, la velocidad de transferencia del gas en el agua ($k_w$) también depende de una el factor beta del transporte aire a agua de CO2 ($\beta$), que a su vez está determinada por el nivel de rugosidad de la superficie.
En resumen, la velocidad de transferencia del gas en el agua ($k_w$) del gas se describe en función de el velocidad del agua ($u_w$), el velocidad del aire ($u_a$), el número de Schmidt ($Sc$), el factor beta del transporte aire a agua de CO2 ($\beta$) y ERROR:9926 de la siguiente manera:
| $ k_w = ( u_a - u_w ) \beta Sc ^ n $ |
ID:(15652, 0)
Solubilidad en función del número de Schmidt
Concepto 
La movilidad de las moléculas, representada por la solubilidad del gas ($\alpha$), se modela como una función de la concentración de las partículas, caracterizada por el número de Schmidt ($Sc$), que a su vez se calcula a partir de los parámetros el viscosidad en masa acuosa ($\eta$), el densidad en capa de masa acuosa ($\rho$), y el constante de difusión en masa acuosa ($D$) utilizando la siguiente expresión:
| $ Sc =\displaystyle\frac{ \eta }{ \rho D }$ |
Esta relación se visualiza en el siguiente diagrama:
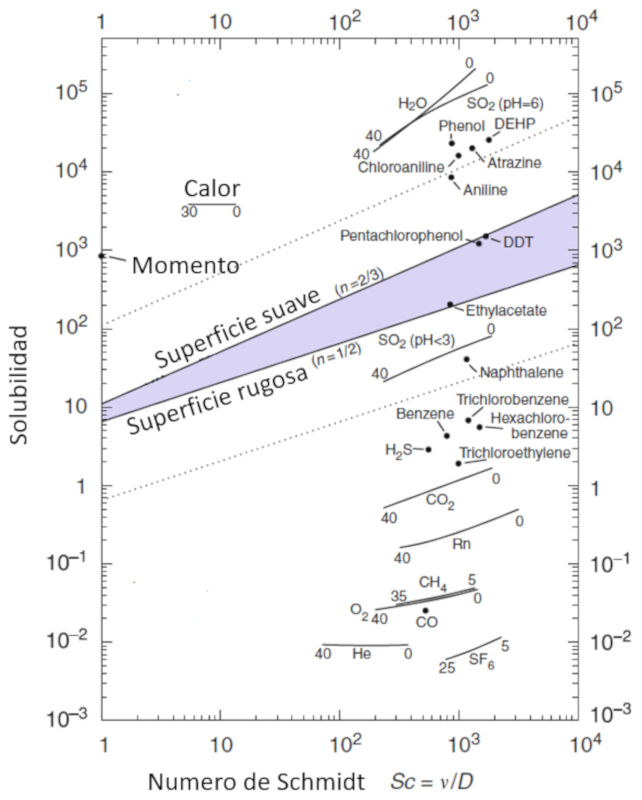
Ocean-Atmosphere Interactions of Gases and Particles, Peter S. Liss, Martin T. Johnson (eds.), Springer-Verlag Berlin Heidelberg
ID:(12245, 0)
Velocidad de transferencia
Concepto 
La velocidad de transferencia del gas en el aire ($k_a$) se puede estimar a partir de la ley de Fick, comparando el constante de difusión en masa acuosa ($D$) con el grosor de la capa superficial ($\delta_c$) de la siguiente manera:
| $ k_a = \displaystyle\frac{ D }{ \delta_c }$ |
ID:(15653, 0)
Velocidad de transferencia y resistencias
Concepto 
Para la interacción entre la atmósfera y el océano, la resistencia de transferencia aire a agua de un gas ($R_{ta}$) engloba inicialmente la resistencia de transferencia en el agua ($R_w$), seguido del proceso de evaporación $1/\alpha$ con la solubilidad del gas ($\alpha$), y una vez que el gas ha pasado al aire, la resistencia de transferencia en el aire ($R_a$) actúa sobre él:
| $ R_{ta} = R_a + \displaystyle\frac{1}{ \alpha } R_w $ |
Mientras tanto, en la interacción entre la atmósfera y el océano, la resistencia de transferencia agua a aire de un gas ($R_{tw}$) inicialmente abarca la resistencia de transferencia en el aire ($R_a$), seguido de la solubilidad del gas ($\alpha$), y una vez que el gas ha penetrado en el agua, la resistencia de transferencia en el agua ($R_w$) actúa:
| $ R_{tw} = R_w + \alpha R_a $ |
Con estas ecuaciones, podemos formular las relaciones para las velocidades de transferencia.
Por lo tanto, utilizando la velocidad de transferencia total del gas en el aire ($k_{ta}$), la velocidad de transferencia del gas en el agua ($k_w$), la velocidad de transferencia del gas en el aire ($k_a$) y la solubilidad del gas ($\alpha$), establecemos la siguiente relación:
| $ \displaystyle\frac{1}{ k_{ta} } = \displaystyle\frac{1}{ k_a } + \displaystyle\frac{1}{ \alpha k_w } $ |
Por otro lado, con la velocidad de transferencia total del gas en el agua ($k_{tw}$), la velocidad de transferencia del gas en el agua ($k_w$), la velocidad de transferencia del gas en el aire ($k_a$) y la solubilidad del gas ($\alpha$), establecemos que:
| $ \displaystyle\frac{1}{ k_{tw} } = \displaystyle\frac{1}{ k_w } + \displaystyle\frac{ \alpha }{ k_a } $ |
ID:(15654, 0)
Modelo de superficie
Modelo 
El intercambio de partículas o moléculas, como el CO2, entre la atmósfera y el océano implica un mecanismo más complejo. Este proceso está relacionado con la formación de una película de líquido saturado con partículas o moléculas, que regula el tránsito de nuevas partículas hacia o desde el interior del océano.
Variables
Cálculos
Cálculos
Ecuaciones
La relaci n entre la resistencia de transferencia aire a agua de un gas ($R_{ta}$), determinada mediante la combinaci n de la resistencia de transferencia en el agua ($R_w$), la resistencia de transferencia en el aire ($R_a$) y la solubilidad del gas ($\alpha$), se formula en la ecuaci n:
| $ R_{ta} = R_a + \displaystyle\frac{1}{ \alpha } R_w $ |
Esto incluye la relaci n de la resistencia de transferencia en el aire ($R_a$) con la velocidad de transferencia del gas en el aire ($k_a$) expresada en:
| $ R_a = \displaystyle\frac{1}{ k_a } $ |
Adem s, la interacci n de la resistencia de transferencia en el agua ($R_w$) con la velocidad de transferencia del gas en el agua ($k_w$) se explica en:
| $ R_w = \displaystyle\frac{1}{ k_w } $ |
Y la relaci n entre la resistencia de transferencia aire a agua de un gas ($R_{ta}$) y la velocidad de transferencia total del gas en el aire ($k_{ta}$) se especifica en:
| $ R_{ta} = \displaystyle\frac{1}{ k_{ta} } $ |
Estos elementos juntos proporcionan la base para definir la relaci n para la velocidad de transferencia total del gas en el aire ($k_{ta}$):
| $ \displaystyle\frac{1}{ k_{ta} } = \displaystyle\frac{1}{ k_a } + \displaystyle\frac{1}{ \alpha k_w } $ |
(ID 12242)
La relaci n entre la resistencia de transferencia agua a aire de un gas ($R_{tw}$), establecida mediante las sumas de la resistencia de transferencia en el agua ($R_w$), la resistencia de transferencia en el aire ($R_a$) y la solubilidad del gas ($\alpha$), se expresa en la ecuaci n:
| $ R_{tw} = R_w + \alpha R_a $ |
Incluyendo la relaci n de la resistencia de transferencia en el aire ($R_a$) con la velocidad de transferencia del gas en el aire ($k_a$) en:
| $ R_a = \displaystyle\frac{1}{ k_a } $ |
La interacci n de la resistencia de transferencia en el agua ($R_w$) con la velocidad de transferencia del gas en el agua ($k_w$) se describe en:
| $ R_w = \displaystyle\frac{1}{ k_w } $ |
Y la conexi n entre la resistencia de transferencia agua a aire de un gas ($R_{tw}$) y la velocidad de transferencia total del gas en el agua ($k_{tw}$) se detalla en:
| $ R_{tw} = \displaystyle\frac{1}{ k_{tw} } $ |
Esto nos proporciona la base para establecer la relaci n para la velocidad de transferencia total del gas en el agua ($k_{tw}$):
| $ \displaystyle\frac{1}{ k_{tw} } = \displaystyle\frac{1}{ k_w } + \displaystyle\frac{ \alpha }{ k_a } $ |
(ID 12243)
Ejemplos
(ID 15640)
Para estudiar la transferencia de CO2 en la superficie del oc ano, es necesario observar detalladamente lo que ocurre con las concentraciones tanto en el aire como en el agua.
En el aire, el CO2 ingresa al agua creando una zona de baja concentraci n en la que disminuye de $C_a$ a $C_{a,0}$. Esta capa tiene un grosor entre 0,1 y 1 mm.
El CO2 que ingresa al agua se acumula inicialmente en la superficie, creando una concentraci n $C_{w,0}$ que luego se difunde hacia el interior, alcanzando una concentraci n menor de $C_w$.
La reducci n de concentraci n permite definir dos zonas: una muy delgada de solo 0,02 a 0,2 mm, donde la concentraci n disminuye r pidamente, y una segunda zona de 0,6 a 2 mm, donde la concentraci n disminuye de manera m s suave hasta alcanzar la concentraci n en el interior del agua.

Ocean-Atmosphere Interactions of Gases and Particles, Peter S. Liss, Martin T. Johnson (eds.), Springer-Verlag Berlin Heidelberg
(ID 12244)
La velocidad de transferencia del gas en el agua ($k_w$) puede ser modelada utilizando datos medidos. En primer lugar, depende de la velocidad a la cual el sistema remueve el carbono de la interfaz aire-agua, lo que hace que la velocidad de transporte sea proporcional a la velocidad relativa entre ambos medios.
En segundo lugar, se presenta un efecto de la movilidad de los iones, que puede describirse mediante el número de Schmidt ($Sc$), representando la relaci n entre la difusi n del impulso y las part culas. Sin embargo, esta dependencia no es lineal y est influenciada por un factor ERROR:9926 que var a entre -1/2 y -2/3 seg n la rugosidad de la superficie.
Finalmente, la velocidad de transferencia del gas en el agua ($k_w$) tambi n depende de una el factor beta del transporte aire a agua de CO2 ($\beta$), que a su vez est determinada por el nivel de rugosidad de la superficie.
En resumen, la velocidad de transferencia del gas en el agua ($k_w$) del gas se describe en funci n de el velocidad del agua ($u_w$), el velocidad del aire ($u_a$), el número de Schmidt ($Sc$), el factor beta del transporte aire a agua de CO2 ($\beta$) y ERROR:9926 de la siguiente manera:
| $ k_w = ( u_a - u_w ) \beta Sc ^ n $ |
(ID 15652)
La movilidad de las mol culas, representada por la solubilidad del gas ($\alpha$), se modela como una funci n de la concentraci n de las part culas, caracterizada por el número de Schmidt ($Sc$), que a su vez se calcula a partir de los par metros el viscosidad en masa acuosa ($\eta$), el densidad en capa de masa acuosa ($\rho$), y el constante de difusión en masa acuosa ($D$) utilizando la siguiente expresi n:
| $ Sc =\displaystyle\frac{ \eta }{ \rho D }$ |
Esta relaci n se visualiza en el siguiente diagrama:

Ocean-Atmosphere Interactions of Gases and Particles, Peter S. Liss, Martin T. Johnson (eds.), Springer-Verlag Berlin Heidelberg
(ID 12245)
La velocidad de transferencia del gas en el aire ($k_a$) se puede estimar a partir de la ley de Fick, comparando el constante de difusión en masa acuosa ($D$) con el grosor de la capa superficial ($\delta_c$) de la siguiente manera:
| $ k_a = \displaystyle\frac{ D }{ \delta_c }$ |
(ID 15653)
Para la interacci n entre la atm sfera y el oc ano, la resistencia de transferencia aire a agua de un gas ($R_{ta}$) engloba inicialmente la resistencia de transferencia en el agua ($R_w$), seguido del proceso de evaporaci n $1/\alpha$ con la solubilidad del gas ($\alpha$), y una vez que el gas ha pasado al aire, la resistencia de transferencia en el aire ($R_a$) act a sobre l:
| $ R_{ta} = R_a + \displaystyle\frac{1}{ \alpha } R_w $ |
Mientras tanto, en la interacci n entre la atm sfera y el oc ano, la resistencia de transferencia agua a aire de un gas ($R_{tw}$) inicialmente abarca la resistencia de transferencia en el aire ($R_a$), seguido de la solubilidad del gas ($\alpha$), y una vez que el gas ha penetrado en el agua, la resistencia de transferencia en el agua ($R_w$) act a:
| $ R_{tw} = R_w + \alpha R_a $ |
Con estas ecuaciones, podemos formular las relaciones para las velocidades de transferencia.
Por lo tanto, utilizando la velocidad de transferencia total del gas en el aire ($k_{ta}$), la velocidad de transferencia del gas en el agua ($k_w$), la velocidad de transferencia del gas en el aire ($k_a$) y la solubilidad del gas ($\alpha$), establecemos la siguiente relaci n:
| $ \displaystyle\frac{1}{ k_{ta} } = \displaystyle\frac{1}{ k_a } + \displaystyle\frac{1}{ \alpha k_w } $ |
Por otro lado, con la velocidad de transferencia total del gas en el agua ($k_{tw}$), la velocidad de transferencia del gas en el agua ($k_w$), la velocidad de transferencia del gas en el aire ($k_a$) y la solubilidad del gas ($\alpha$), establecemos que:
| $ \displaystyle\frac{1}{ k_{tw} } = \displaystyle\frac{1}{ k_w } + \displaystyle\frac{ \alpha }{ k_a } $ |
(ID 15654)
(ID 15645)
ID:(1633, 0)
