Benützer:


Brechende Wellen
Storyboard

Die Luftströmungen über dem Ozean treiben die Bewegung des Wassers an und erzeugen Wellen, die je nach Tiefe unterschiedlich auf Schwankungen reagieren. Dieses Phänomen ist als Wellenbrechen bekannt. Das Wellenbrechen tritt auf, weil die Ausbreitungsgeschwindigkeit einer Welle in tieferen Gebieten größer ist. Daher überholen beim Nähern an die Küste die Wellen aus tieferen Bereichen jene aus flacheren, was zum charakteristischen Brechen der Wellen führt.

>Modell

ID:(1632, 0)


Mechanismen
Konzept


ID:(15639, 0)


Wellenbruch am Strand
Beschreibung

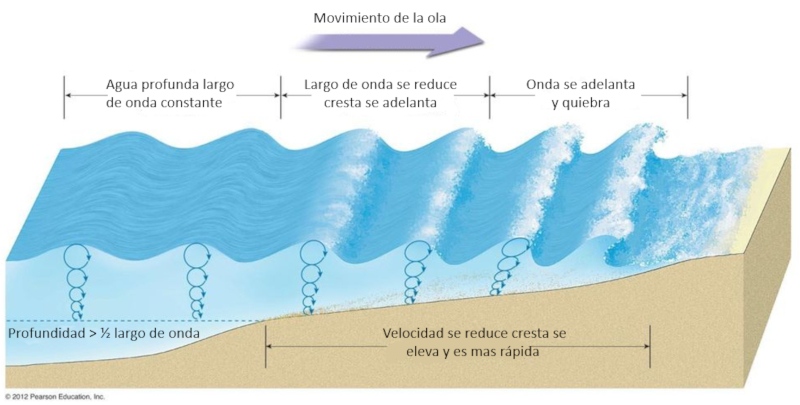
Wenn eine Welle den Strand erreicht, beginnt sie den Strandhang hinaufzusteigen und wird dabei allmählich flacher, wodurch sie langsamer wird. Eine folgende Welle neigt dazu, sich über der vorhergehenden Welle zu erheben. Da das Wasser in dieser Situation tiefer wird, ist die zweite Welle schneller und neigt dazu, die zuvor angekommene Welle zu überholen. Diese Wechselwirkung führt letztendlich dazu, dass die Welle bricht und das Phänomen entsteht, das als Brechen der Welle bekannt ist.

ID:(12308, 0)


Winkelfrequenz
Konzept

Wenn man sich daran erinnert, dass die Winkelgeschwindigkeit den pro Zeiteinheit zurückgelegten Winkel darstellt, kann man erkennen, dass der Ausdruck

$\displaystyle\frac{2\pi}{T}$



einer vollständigen Umdrehung ($2\pi$) entspricht, geteilt durch die Zeit die Zeit ($T$), die für einen Zyklus benötigt wird. Daher wird die Winkelfrequenz ($\omega$) definiert als

$ \omega = \displaystyle\frac{2 \pi }{ T }$

ID:(15648, 0)


Wellenvektor
Konzept

Der Wellenvektor ($k$) ist der Faktor, der die Position multipliziert und entspricht dem Wert, bei dem, wenn sich die Welle entlang ein Wellenlänge ($\lambda$) bewegt, sie dieselbe Form annimmt, die sie ursprünglich hatte. Damit dies geschieht, muss folgende Bedingung erfüllt sein:

$kx = k\lambda = 2\pi$



Daher haben wir mit der Wellenlänge ($\lambda$) festgelegt:

$ k =\displaystyle\frac{2 \pi }{ \lambda }$

ID:(15647, 0)


Wellenphasengeschwindigkeit
Konzept

Die Geschwindigkeit von Wellen hängt von der Wassertiefe und dem Faktor der Wellenvektor ($k$) ab, der mit der Wellenlänge ($\lambda$) wie folgt berechnet wird:

$ k =\displaystyle\frac{2 \pi }{ \lambda }$



Bezüglich der Phasengeschwindigkeit ($c_p$), das die Geschwindigkeit darstellt, mit der sich jede Wellenkrone bewegt, kann dies mit der Meerestiefe ($h$) und die Gravitationsbeschleunigung ($g$) bestimmt werden. Der Phasengeschwindigkeit ($c_p$) wird wie folgt berechnet:

$ c_p =\sqrt{\displaystyle\frac{ g }{ k } \tanh( k h )}$

Die Phasengeschwindigkeit bezieht sich auf die Geschwindigkeit, mit der eine bestimmte Schwingung oder Welle sich bewegt.

ID:(15649, 0)


Wellengruppengeschwindigkeit
Konzept

Wellen haben eine Geschwindigkeit, die von der Wassertiefe und dem Faktor der Wellenvektor ($k$) abhängt, berechnet mit der Wellenlänge ($\lambda$) wie folgt:

$ k =\displaystyle\frac{2 \pi }{ \lambda }$



Für der Gruppengeschwindigkeit ($c_g$), die die Geschwindigkeit repräsentiert, mit der sich der gesamte Wellenzug bewegt und nicht jede einzelne Welle, kann sie mit der Phasengeschwindigkeit ($c_p$) berechnet werden. Diese wird mit der Meerestiefe ($h$) und die Gravitationsbeschleunigung ($g$) auf folgende Weise bestimmt:

$ c_p =\sqrt{\displaystyle\frac{ g }{ k } \tanh( k h )}$



Schließlich kann der Gruppengeschwindigkeit ($c_g$) mit der folgenden Formel berechnet werden:

$ c_g =\displaystyle\frac{ c_p }{2}\left(1 + \displaystyle\frac{2 k h }{\sinh(2 k h )}\right)$

Die Gruppengeschwindigkeit ist die Geschwindigkeit, mit der sich der Wellenzug oder eine Gruppe von Wellen im Wassermedium bewegt.

ID:(15650, 0)


Wellengeschwindigkeiten
Bild

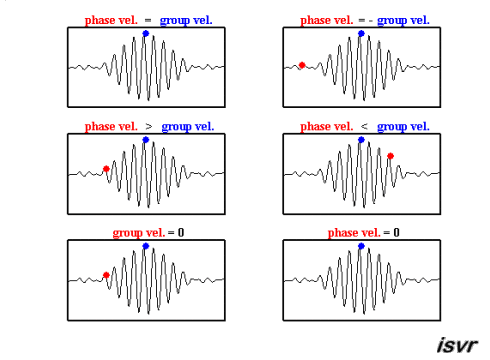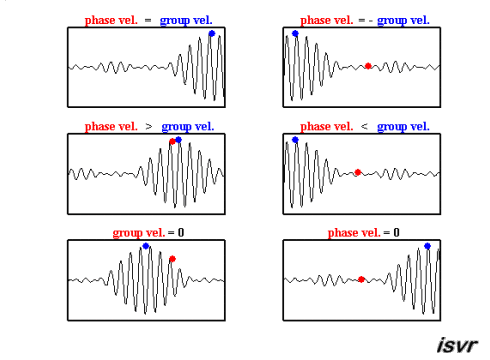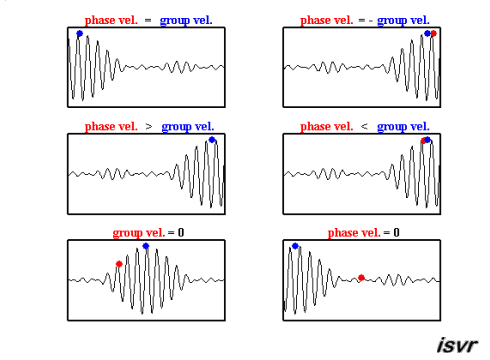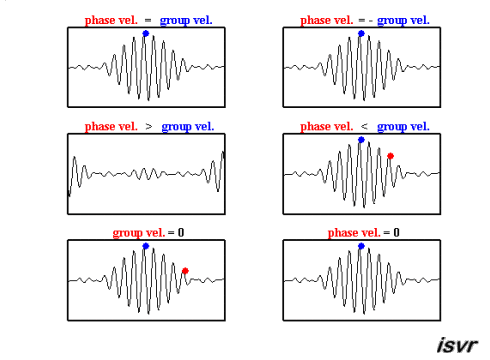
In der Wellenmechanik gibt es zwei charakteristische Geschwindigkeiten. Einerseits haben wir die Geschwindigkeit, mit der sich eine bestimmte Welle bewegt, die abhängig von der Frequenz variieren kann und sich somit von einer Welle zur anderen unterscheidet.

Die zweite Art von Geschwindigkeit, die beobachtet wird, ist die eines Wellenpakets, d.h. einer Gruppe von Wellen unterschiedlicher Frequenzen und Phasen, die sich überlagern und einen Verbund bilden, der sich als Einheit bewegt. Diese Geschwindigkeit wird als Gruppengeschwindigkeit bezeichnet.

Beide Geschwindigkeiten können in dieser Animation beobachtet werden:

ID:(15651, 0)


Wellenbeschreibung
Konzept

Eine Welle lässt sich näherungsweise als eine Sinusfunktion in Abhängigkeit von den Variablen der Position ($x$) und der Zeit ($t$) beschreiben.

Die Funktion berücksichtigt die Werte von der Wellenhöhe ($u$) an jedem Punkt sowie der Maximale Wellenhöhe ($z_0$), der Wellenvektor ($k$) und der Frecuencia angular ($\omega$):

$ u( x , t ) = z_0 \cos( k x - \omega t )$

ID:(15646, 0)


Modell
Konzept


ID:(15644, 0)


Brechende Wellen
Modell

Die Luftströmungen über dem Ozean treiben die Bewegung des Wassers an und erzeugen Wellen, die je nach Tiefe unterschiedlich auf Schwankungen reagieren. Dieses Phänomen ist als Wellenbrechen bekannt. Das Wellenbrechen tritt auf, weil die Ausbreitungsgeschwindigkeit einer Welle in tieferen Gebieten größer ist. Daher überholen beim Nähern an die Küste die Wellen aus tieferen Bereichen jene aus flacheren, was zum charakteristischen Brechen der Wellen führt.

Variablen
Symbol
Text
Variable
Wert
Einheiten
Berechnen
MKS-Wert
MKS-Einheiten
$\omega$
omega
Frecuencia angular
rad/s
$c_g$
c_g
Gruppengeschwindigkeit
m/s
$v_{\omega,x}$
v_wx
Horizontale Geschwindigkeit der Welle
m/s
$z_0$
z_0
Maximale Wellenhöhe
m
$h$
h
Meerestiefe
m
$c_p$
c_p
Phasengeschwindigkeit
m/s
$z$
z
Position
m
$x$
x
Position
m
$v_{\omega,z}$
v_wz
Vertikale Geschwindigkeit der Welle
m/s
$v_{\omega}$
v_w
Wellengeschwindigkeit
m/s
$u$
u
Wellenhöhe
m
$\lambda$
lambda
Wellenlänge
m
$k$
k
Wellenvektor
1/m
$T$
T
Zeit
s
$t$
t
Zeit
s

Berechnungen

Zuerst die Gleichung auswählen:   zu ,  dann die Variable auswählen:   zu 
Symbol
Gleichung
Gelöst
Übersetzt

Berechnungen

Symbol
Gleichung
Gelöst
Übersetzt

 Variable   Gegeben   Berechnen   Ziel :   Gleichung   Zu verwenden


Gleichungen

Beispiele


(ID 15639)

Wenn eine Welle den Strand erreicht, beginnt sie sich zu heben, w hrend sie die Strandneigung hinaufl uft. Dabei wird sie zunehmend flacher und dadurch langsamer. Eine nachfolgende zweite Welle neigt dazu, sich ber die vorherige zu schieben. Da das Wasser in dieser Zone tiefer ist, bewegt sich die zweite Welle schneller und berholt tendenziell die erste, die zuvor am Ufer ankam. Diese Wechselwirkung zwischen den Wellen f hrt zum Brechen der Welle und erzeugt das Ph nomen, das als Brandung bekannt ist.



Dieses Ph nomen kann durch die Beschreibung von der Wellenhöhe ($u$) mithilfe einer der Maximale Wellenhöhe ($z_0$)-Welle modelliert werden, die sich mit einem der Wellenvektor ($k$) und der Frecuencia angular ($\omega$) ausbreitet. Der Ausdruck f r der Position ($x$) und der Zeit ($t$) ist:

$ u( x , t ) = z_0 \cos( k x - \omega t )$



Das Wasser selbst f hrt eine Kreisbewegung aus, deren Geschwindigkeit die Beziehungen mit die Wellengeschwindigkeit ($v_{\omega}$) und der Meerestiefe ($h$) erf llt:

$ v_{\omega,x} = v_{\omega} \cosh( k ( z + h )) \cos( k x - \omega t )$



und

$ v_{\omega,z} = v_{\omega} \sinh( k ( z + h )) \sin( k x - \omega t )$

(ID 12308)

Wenn man sich daran erinnert, dass die Winkelgeschwindigkeit den pro Zeiteinheit zur ckgelegten Winkel darstellt, kann man erkennen, dass der Ausdruck

$\displaystyle\frac{2\pi}{T}$



einer vollst ndigen Umdrehung ($2\pi$) entspricht, geteilt durch die Zeit die Zeit ($T$), die f r einen Zyklus ben tigt wird. Daher wird die Winkelfrequenz ($\omega$) definiert als

$ \omega = \displaystyle\frac{2 \pi }{ T }$

(ID 15648)

Der Wellenvektor ($k$) ist der Faktor, der die Position multipliziert und entspricht dem Wert, bei dem, wenn sich die Welle entlang ein Wellenlänge ($\lambda$) bewegt, sie dieselbe Form annimmt, die sie urspr nglich hatte. Damit dies geschieht, muss folgende Bedingung erf llt sein:

$kx = k\lambda = 2\pi$



Daher haben wir mit der Wellenlänge ($\lambda$) festgelegt:

$ k =\displaystyle\frac{2 \pi }{ \lambda }$

(ID 15647)

Die Wellengeschwindigkeit h ngt von der Wassertiefe und dem Faktor die Winkelfrequenz ($\omega$) ab, der aus der Phasengeschwindigkeit ($c_p$) und der Wellenvektor ($k$) wie folgt bestimmt wird:

$ \omega = c_p k $



Bez glich der Phasengeschwindigkeit ($c_p$), das die Geschwindigkeit angibt, mit der sich jede Wellenkuppe fortbewegt, l sst sich dieser Wert mithilfe von der Meerestiefe ($h$) und die Gravitationsbeschleunigung ($g$) berechnen. Der Wert von der Phasengeschwindigkeit ($c_p$) ergibt sich aus:

$ c_p =\sqrt{\displaystyle\frac{ g }{ k } \tanh( k h )}$

In diesem Zusammenhang bezeichnet die Phasengeschwindigkeit die Geschwindigkeit, mit der sich eine einzelne Schwingung oder Welle ausbreitet.

(ID 15649)

Wellen haben eine Geschwindigkeit, die von der Wassertiefe und dem Faktor der Wellenvektor ($k$) abh ngt, berechnet mit der Wellenlänge ($\lambda$) wie folgt:

$ \omega = c_p k $



F r der Gruppengeschwindigkeit ($c_g$), die die Geschwindigkeit repr sentiert, mit der sich der gesamte Wellenzug bewegt und nicht jede einzelne Welle, kann sie mit der Phasengeschwindigkeit ($c_p$) berechnet werden. Diese wird mit der Meerestiefe ($h$) und die Gravitationsbeschleunigung ($g$) auf folgende Weise bestimmt:

$ c_g = \displaystyle\frac{d \omega }{d k }$



Schlie lich kann der Gruppengeschwindigkeit ($c_g$) mit der folgenden Formel berechnet werden:

$ c_g =\displaystyle\frac{ c_p }{2}\left(1 + \displaystyle\frac{2 k h }{\sinh(2 k h )}\right)$

Die Gruppengeschwindigkeit ist die Geschwindigkeit, mit der sich der Wellenzug oder eine Gruppe von Wellen im Wassermedium bewegt.

(ID 15650)

In der Wellenmechanik gibt es zwei charakteristische Geschwindigkeiten. Einerseits haben wir die Geschwindigkeit, mit der sich eine bestimmte Welle bewegt, die abh ngig von der Frequenz variieren kann und sich somit von einer Welle zur anderen unterscheidet.

Die zweite Art von Geschwindigkeit, die beobachtet wird, ist die eines Wellenpakets, d.h. einer Gruppe von Wellen unterschiedlicher Frequenzen und Phasen, die sich berlagern und einen Verbund bilden, der sich als Einheit bewegt. Diese Geschwindigkeit wird als Gruppengeschwindigkeit bezeichnet.

Beide Geschwindigkeiten k nnen in dieser Animation beobachtet werden:

(ID 15651)


(ID 15644)

ID:(1632, 0)