Usuario:
Radiación infrarroja
Storyboard 
La radiación infrarroja corresponde principalmente a la energía irradiada por la tierra. Una pequeña parte de esta es irradiada directamente al espacio mientras que la gran mayoría es absorbida por las nubes. Estas a su vez irradian tanto devuelta a la tierra como al espació. El origen del calentamiento global es principalmente una consecuencia de este flujo de la tierra a la atmósfera y de esta ultima a la superficie de la tierra.
ID:(536, 0)
Balance de radiación infrarroja
Imagen
Al calentarse el planeta con la radiación absorbida
La atmósfera en si es modelada como un sistema con una parte superior, que absorbe radiación visible
Finalmente se tienen otros fenómeno como conducción y convección que hacen que exista un flujo de energía adicional de la superficie de la tierra a la parte inferior de la nube. La intensidad asociada la denominamos
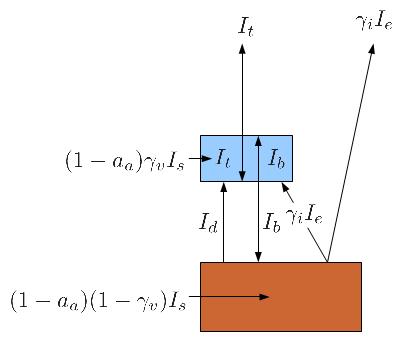
Balance infrarrojo
ID:(3074, 0)
Emisividad de la tierra
Imagen
La emisividad de la superficie fluctuar entre 0.7 (océano), 0.8 (desiertos), 0.9 (nieve) y 1.0 (vegetación):
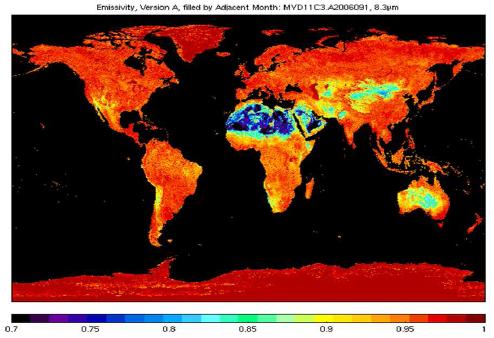
ID:(3073, 0)
Temperatura de la superficie
Imagen
Al asociar la ley de Stefan Boltzmann la temperatura de un cuerpo con la radiación emitida, se puede usar esta ultima para determinar la temperatura de la superficie del planeta:
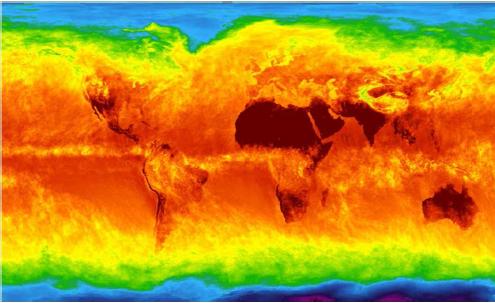
Temperatura del planeta
ID:(3075, 0)
Emisión Intensidad NIR de la superficie del planeta al espacio
Ecuación
Al igual que ocurre con la radiación visible, la atmósfera interactúa con la radiación infrarroja. De manera similar a cómo se modela la interacción con la atmósfera en el caso de la radiación visible utilizando la cobertura visible (VIS) ($\gamma_v$), se puede introducir cobertura infrarroja (NIR) ($\gamma_i$) que afecta a la radiación infrarroja.
Por ello, la intensidad NIR emitida por la tierra al espacio ($I_{es}$) es igual a la intensidad NIR emitida por la tierra ($I_e$) ponderado por un factor que depende de cobertura infrarroja (NIR) ($\gamma_i$), de modo que:
| $ I_{es} =(1- \gamma_i ) I_e $ |
ID:(4677, 0)
Emisión intensidad NIR de la tierra a la atmósfera
Ecuación
De la radiación terrestre $I_e$, que en su mayoría
| $\lambda > 750\,nm$ |
La fracción de radiación que interactúa con la atmósfera se calcula utilizando la cobertura $\gamma$ mediante
| $ I_{esa} = \gamma_i I_e $ |
ID:(4684, 0)
Emisión intensidad NIR de la superficie de la tierra
Ecuación
Si la Tierra está a una temperatura $T_e$, emite radiación de acuerdo con la ley de Stefan-Boltzmann con una intensidad dada por la siguiente fórmula:
donde $\sigma$ es la constante de Stefan-Boltzmann y $\epsilon$ es el coeficiente de emisividad. La constante de Stefan-Boltzmann $\sigma$ tiene un valor de aproximadamente $5.67 \times 10^{-8} W/m^2K^4$ y el coeficiente de emisividad $\epsilon$ representa la eficiencia con la que la superficie terrestre emite radiación, siendo un valor entre 0 y 1.
ID:(4676, 0)
Emisión intensidad NIR a de la parte inferior de la atmósfera
Ecuación
La intensidad $I$ emitida por un cuerpo a temperatura $T$ se rige por la ley de Stefan-Boltzmann, que se expresa como:
| $ I_b = \sigma \epsilon T_b ^4$ |
donde $\epsilon$ es la emisividad y $\sigma$ es la constante de Stefan-Boltzmann. Por lo tanto, en el caso del borde inferior de la nube, que tiene una temperatura $T_b$, la intensidad será:
ID:(4679, 0)
Emisión intensidad NIR de la parte superior de la atmósfera
Ecuación
Si la parte superior de la atmósfera esta a una temperatura $T_t$, emite radiación, en su mayoría
| $\lambda > 750\,nm$ |
según a la ley de Stefan Boltzmann
| $ I_t = \sigma \epsilon T_t ^4$ |
donde $\sigma$ es la constante de Stefan Boltzmann y $\epsilon$ el coeficiente de emisividad.
ID:(4680, 0)
Distribución de calor transportado por convección
Descripción
Si observamos la distribución del calor transportado por convección en la superficie del planeta, se puede notar que existen niveles más o menos constantes. Por un lado, tenemos las zonas oceánicas y continentales con un flujo de alrededor de $17 W/m^2$ (ascendente) y aproximadamente $-30 W/m^2$ (descendente) en las áreas cubiertas de nieve y hielo:
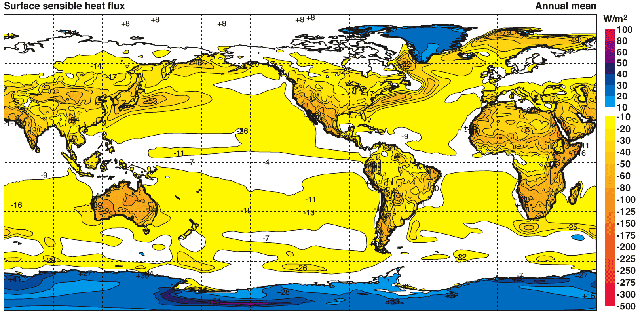
Promedio anual de calor transportado por convección calculado de ECMWF 40-años re analizados (Kallberg et al 2005). Cuidado: este diagrama usa la convención de que un flujo ascendente es negativo a diferencia que el presente texto que la define como positiva.
Estos datos provienen de una reanálisis de 40 años realizado por Kallberg P., Berrisford P., Hoskins B., Simmons A., Uppala S., Lamy-Thepaut S., Hine R., 2005: ERA-40 Atlas. Reading, Reino Unido, ECMWF Re-Analysis Project (Kallberg et al., 2005).
ID:(9263, 0)
Emisión onda larga de la tierra en función del tiempo (D0+1)
Php
Si se observa la radiación de onda larga (NIR) se ve que existe un máximo en torno al mes de agosto/septiembre de todos los años:
Esto se debe a que el hemisferio norte presenta mayor masas continentales por lo que estas reflejan mayormente cuando es verano en dicho hemisferio..
ID:(9324, 0)
Emisión onda larga de la tierra en función de la latitud (D1+0)
Php
La radiación de onda larga (NIR) es en primera aproximación simétrica en torno al ecuador fuera de presentar un máximo en torno de los grados -20 y +20:
Esto corresponde tanto a la falta de masa continental en torno al ecuador y la baja de intensidad hacia los polos por efecto de la incidencia inclinada de la radiación.
ID:(9325, 0)
Flujo conducción y evaporación
Concepto
By modeling la energía transmitido por conducción y evaporación ($I_d$), a relationship for heat transport can be established that includes the difference between la temperatura de la superficie de la tierra ($T_e$) and la temperatura de la parte inferior de la atmósfera ($T_b$) and la velocidad del viento ($u$), which is key in the process. The equation involves two constants, el coeficiente de calor latente ($\kappa_l$) and el coeficiente de convección ($\kappa_c$), such that:
| $ I_d =( \kappa_l + \kappa_c ( T_e - T_b )) u $ |
el coeficiente de calor latente ($\kappa_l$) is on the order of 10.0 W/m² and el coeficiente de convección ($\kappa_c$) is on the order of 0.16 W/m²K, with la velocidad del viento ($u$) typically being around 8 m/s.
el coeficiente de calor latente ($\kappa_l$) primarily comes from the energy transported by moving masses of moist air, which release energy when condensed. El coeficiente de convección ($\kappa_c$) originates from the transport of air through convection and the corresponding adiabatic expansion, so it mainly depends on the temperature gradient.
ID:(15682, 0)
Modelo
Top
Parámetros
Variables
Cálculos
a 
, luego, seleccione la variable: 
a 
Cálculos
Cálculos
Variable 
Dado Calcule 
Objetivo : Ecuación A utilizar 
Ecuaciones
$ I_e = \sigma \epsilon T_e ^4$
I = s * e * T ^4
$ I_b = \sigma \epsilon T_b ^4$
I = s * e * T ^4
$ I_t = \sigma \epsilon T_t ^4$
I = s * e * T ^4
$ I_b = \epsilon \sigma T_b ^4 $
I_b = e * s * T_b ^4
$ I_d =( \kappa_l + \kappa_c ( T_e - T_b )) u $
I_d =( k_l + k_c *( T_e - T_b ))* u
$ I_e = \epsilon \sigma T_e ^4 $
I_e = e * s * T_e ^4
$ I_{es} =( 1 - \gamma_i ) I_e $
I_es =( 1 - g_i )* I_e
$ I_{esa} = \gamma_i I_e $
I_esa = g_i * I_e
$ I_{esa} = \gamma_i I_e $
I_i = g * I_s
$ I_t = \epsilon \sigma T_t ^4 $
I_t = e * s * T_t ^4
$ I_{es} =(1- \gamma_i ) I_e $
I_t =(1- g )* I_s
ID:(15678, 0)
Intensidad que interactúa
Ecuación
La intensidad que interactua ($I_i$) es la fracción definida por factor de interacción ($\gamma$) de la intensidad incidente ($I_s$), calculada de la siguiente manera:
| $ I_{esa} = \gamma_i I_e $ |
| $ I_i = \gamma I_s $ |
ID:(9986, 0)
Intensidad que no interactúa
Ecuación
La intensidad transmitida ($I_t$) es igual a la intensidad incidente ($I_s$) disminuido por factor de interacción ($\gamma$), de modo que se obtiene:
| $ I_{es} =(1- \gamma_i ) I_e $ |
| $ I_t =(1- \gamma ) I_s $ |
ID:(10324, 0)
Intensidad en función de la temperatura (1)
Ecuación
La Ley de Stefan-Boltzmann establece que la intensidad irradiada ($I$) es una función de la temperatura ($T$), utilizando las constantes la emisividad ($\epsilon$) y la constante de Stefan Boltzmann ($\sigma$), de la siguiente manera:
| $ I_e = \sigma \epsilon T_e ^4$ |
| $ I = \sigma \epsilon T ^4$ |
ID:(14479, 1)
Intensidad en función de la temperatura (2)
Ecuación
La Ley de Stefan-Boltzmann establece que la intensidad irradiada ($I$) es una función de la temperatura ($T$), utilizando las constantes la emisividad ($\epsilon$) y la constante de Stefan Boltzmann ($\sigma$), de la siguiente manera:
| $ I_b = \sigma \epsilon T_b ^4$ |
| $ I = \sigma \epsilon T ^4$ |
ID:(14479, 2)
Intensidad en función de la temperatura (3)
Ecuación
La Ley de Stefan-Boltzmann establece que la intensidad irradiada ($I$) es una función de la temperatura ($T$), utilizando las constantes la emisividad ($\epsilon$) y la constante de Stefan Boltzmann ($\sigma$), de la siguiente manera:
| $ I_t = \sigma \epsilon T_t ^4$ |
| $ I = \sigma \epsilon T ^4$ |
ID:(14479, 3)
Flujo conducción y evaporación
Ecuación
La energía transmitido por conducción y evaporación ($I_d$) depende de la diferencia entre la temperatura de la parte inferior de la atmósfera ($T_b$) y la temperatura de la superficie de la tierra ($T_e$), así como de la velocidad del viento ($u$) y las constantes el coeficiente de calor latente ($\kappa_l$) y el coeficiente de convección ($\kappa_c$), de la siguiente manera:
| $ I_d =( \kappa_l + \kappa_c ( T_e - T_b )) u $ |
ID:(9270, 0)