User:
Cause of variation in salinity
Description 
When analyzing salinity and the balance between rainfall and evaporation, the following relationships can be observed:
A: In areas where there is a greater reduction of water due to higher rates of evaporation compared to rainfall, higher salinity is observed. This is because as water evaporates, minerals and dissolved salts in the water become more concentrated, increasing salinity in the area. This situation often occurs in arid or semi-arid regions where evaporation is high and precipitation is limited.
B: On the other hand, in areas where there is a greater contribution of water due to higher rates of rainfall compared to evaporation, lower salinity is observed. This is because rainfall brings fresh water that dilutes salts and reduces the concentration of dissolved minerals in the soil and water bodies. These areas are typically regions with high precipitation or in proximity to freshwater sources such as rivers or lakes.
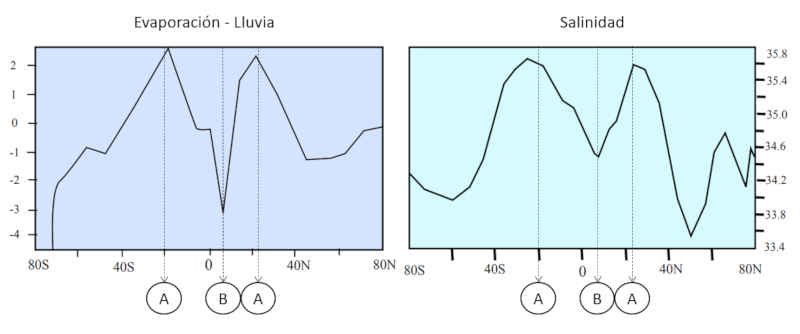
This image illustrates the relationship between salinity and the balance of rainfall and evaporation. In areas where evaporation exceeds rainfall, salinity tends to be high, while in areas where rainfall exceeds evaporation, salinity tends to be low.
It is important to note that other factors such as geology, groundwater circulation, and ocean currents can also influence the salinity of specific regions. However, the balance between rainfall and evaporation is a key factor in understanding variations in salinity in different areas.
ID:(12370, 0)
Salinity and temperature relationship
Description
Observing salinity and temperature measurements at different depths (in this case, at a latitude of 9 degrees south), a relationship with two points of inflection can be observed:
- From the surface to a depth of 800 m, there is a simultaneous increase in temperature and salinity.
- Descending further to 2000 m, the temperature remains constant while the salinity decreases.
- Beyond 2000 m, both temperature and salinity continue to increase with depth.
Interestingly, this behavior occurs within a range of 4 degrees, which corresponds to the temperature at which fresh water reaches its maximum density. One can interpret the range from 800 m to 2000 m as a depth where water 'expels salt' similar to a phase change. Therefore, to understand this behavior, it is necessary to first assess the entropy's behavior.
ID:(12371, 0)
Specific volume
Equation
The challenge of working with volume in the case of seawater is that it depends on variations in temperature, salinity, and pressure. On the other hand, mass is less affected by these variations, which is why it makes sense to work with what we call specific volume, calculated by dividing the volume $V$ by the mass $M$:
$\displaystyle\frac{V}{M}$
However, $M/V$ represents density, so the specific volume is defined as:
 $ \alpha = \displaystyle\frac{1}{ \rho }$ |
ID:(11984, 0)
Thermal expansion coefficient of ocean water
Equation
In the case of the ocean, the concept of specific volume $\alpha$ is used instead of the thermal expansion coefficient $k_T$. Therefore, it is necessary to convert the thermal expansion coefficient, which is typically defined in terms of volume change, into terms of specific volume change. Thus, for a temperature variation $T$, the thermal expansion coefficient in terms of specific volume $\alpha$ can be expressed as follows:
| $ k_T =\displaystyle\frac{1}{ \alpha }\left(\displaystyle\frac{ \partial\alpha }{ \partial T }\right)_{ p , S }$ |
The thermal expansion coefficient is defined by
| $ k_T = +\displaystyle\frac{1}{ V }\displaystyle\left(\displaystyle\frac{\partial V }{\partial T }\displaystyle\right)_ p $ |
In the case of oceanic water, we work with the specific volume
| $ \alpha = \displaystyle\frac{1}{ \rho }$ |
instead of the volume $V$. Therefore, a change of variable can be made, resulting in the thermal expansion coefficient as
| $ k_T =\displaystyle\frac{1}{ \alpha }\left(\displaystyle\frac{ \partial\alpha }{ \partial T }\right)_{ p , S }$ |
.
ID:(11980, 0)
Ocean water compressibility coefficient
Equation
In the case of the ocean, the concept of specific volume $\alpha$ is used instead of the compressibility coefficient $k_p$. Therefore, it is necessary to convert the compressibility coefficient, which is typically defined in terms of volume variation, into terms of specific volume variation. Thus, in response to a pressure variation $p$, the compressibility coefficient in terms of specific volume $\alpha$ can be expressed as:
| $ k_p = -\displaystyle\frac{1}{ \alpha }\left(\displaystyle\frac{ \partial\alpha }{ \partial p }\right)_{ T , S }$ |
The compressibility coefficient with $k_p$ is defined by
| $ k_p = -\displaystyle\frac{1}{ V }\displaystyle\left(\displaystyle\frac{\partial V }{\partial p }\displaystyle\right)_ T $ |
In the case of oceanic water, we work with the specific volume
| $ \alpha = \displaystyle\frac{1}{ \rho }$ |
instead of the volume $V$. Therefore, a change of variable can be performed, resulting in the compressibility coefficient as
| $ k_p = -\displaystyle\frac{1}{ \alpha }\left(\displaystyle\frac{ \partial\alpha }{ \partial p }\right)_{ T , S }$ |
ID:(11981, 0)
Haline contraction coefficient
Equation
The contraction coefficient due to salinity should have a similar form to the compressibility and thermal expansion coefficients. However, instead of observing the volume variation due to pressure or temperature, in this case, it relates to the variation in salinity.
In the case of the ocean, we work with the specific volume $\alpha$ instead of the traditional volume $V$. Therefore, the contraction coefficient should have the following form:
| $ k_i = -\displaystyle\frac{1}{ \alpha }\left(\displaystyle\frac{ \partial\alpha }{ \partial i }\right)_{ p , T }$ |
The negative sign is associated with the fact that an increase in salinity leads to an increase in density. However, the specific volume is equal to the inverse of density, and therefore, an increase in density is associated with a reduction in specific volume.
ID:(11982, 0)
Equation of state of marine water simplify
Equation
The specific volume $\alpha$ varies with changes in temperature $T$, salinity $i$, and pressure $p$ individually. If we assume that the total change resulting from simultaneous variations in multiple variables can be expressed as the sum of the individual changes:
| $ \displaystyle\frac{ d\alpha }{ \alpha }= k_T dT - k_i di - k_p dp$ |
The variation of temperature $T$ is governed by the equation of the thermal expansion coefficient $k_T$:
| $ k_T =\displaystyle\frac{1}{ \alpha }\left(\displaystyle\frac{ \partial\alpha }{ \partial T }\right)_{ p , S }$ |
The variation of salinity $i$ is governed by the equation of the salt concentration coefficient:
| $ k_i = -\displaystyle\frac{1}{ \alpha }\left(\displaystyle\frac{ \partial\alpha }{ \partial i }\right)_{ p , T }$ |
Finally, the variation of pressure $p$ is governed by the equation of the compressibility coefficient:
| $ k_p = -\displaystyle\frac{1}{ \alpha }\left(\displaystyle\frac{ \partial\alpha }{ \partial p }\right)_{ T , S }$ |
Therefore, the total variation of specific volume $\alpha$ can be estimated as the sum of the individual variations:
$d\alpha = d\alpha_T + d\alpha_i +d\alpha_p$
Thus, the total variation can be generalized as:
| $ \displaystyle\frac{ d\alpha }{ \alpha }= k_T dT - k_i di - k_p dp$ |
ID:(11983, 0)