Storyboard

>Model

ID:(1535, 0)

Equation

>Top, >Model

The contraction coefficient due to salinity should have a similar form to the compressibility and thermal expansion coefficients. However, instead of observing the volume variation due to pressure or temperature, in this case, it relates to the variation in salinity.

In the case of the ocean, we work with the specific volume $\alpha$ instead of the traditional volume $V$. Therefore, the contraction coefficient should have the following form:

$k_i = -\displaystyle\frac{1}{ \alpha }\left(\displaystyle\frac{ \partial\alpha }{ \partial i }\right)_{ p , T }$

Conditions

Variables

$k_i$

Coeficiente de contracción halina

$-$

9360

$i$

Salinidad

$-$

9352

$\alpha$

Volumen especifico

$m^3/kg$

9396

$\alpha_0$

Volumen especifico base

$m^3/kg$

9397

Relation

The negative sign is associated with the fact that an increase in salinity leads to an increase in density. However, the specific volume is equal to the inverse of density, and therefore, an increase in density is associated with a reduction in specific volume.

ID:(11982, 0)

Description

>Top

The compressibility coefficient for oceanic water, measured as a function of salinity, exhibits the trend shown in the following graph:

In general, it is observed that compressibility:

- decreases with increasing salinity.

- decreases with increasing temperature.

ID:(11989, 0)

Description

>Top

The concentration coefficient for oceanic water, measured as a function of salinity, exhibits the trend shown in the following graph:

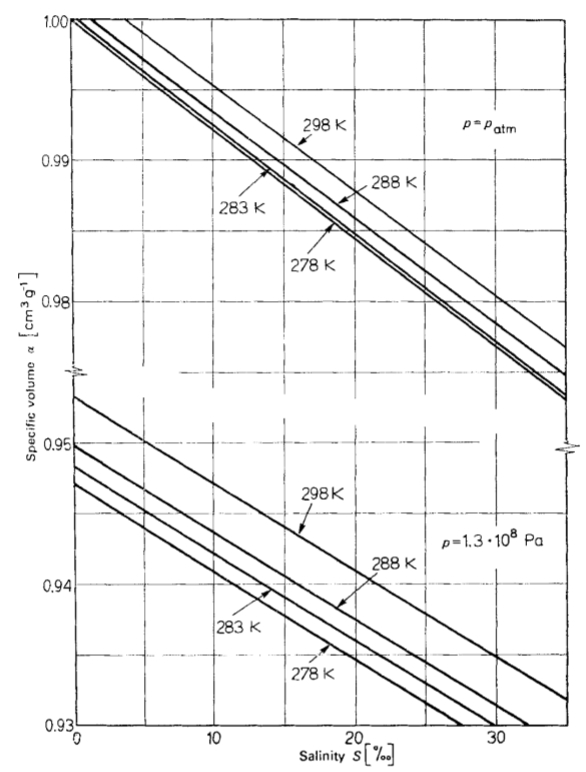
Two groups of curves can be observed, one at shallow depth ($1 atm$) and the other at high depth ($1.3\times 10^8 Pa$). The difference is that at greater depths, the specific volume is smaller.

For both cases, it is observed that the specific volume:

- decreases with increasing salinity.

- decreases with increasing temperature.

ID:(11990, 0)