Oscilaciones de las moléculas de agua
Descripción 
Las moléculas de agua tienen la capacidad de oscilar en varios modos diferentes.
• Cuando una onda de luz con una frecuencia que coincide con la del modo de oscilación se presenta, ocurren dos eventos:
• El modo de oscilación de la molécula se activa, lo que significa que la molécula comienza a vibrar en el modo correspondiente.
La energía necesaria para activar el modo de oscilación se obtiene de la onda de luz, lo que resulta en una reducción en la intensidad de la luz.
En otras palabras, cuando una onda de luz coincide con la frecuencia de oscilación de una molécula de agua, esa molécula absorbe la energía de la luz y entra en un estado de vibración específico. Este fenómeno es fundamental en varios procesos relacionados con la interacción de la luz con el agua, como la absorción de luz en el espectro visible y la dispersión de la luz en fenómenos ópticos como el arcoíris.

ID:(12467, 0)
Espectro de la luz solar
Descripción 
Cuando la luz que llega a la Tierra es absorbida, se producen disminuciones en la intensidad del espectro observado:
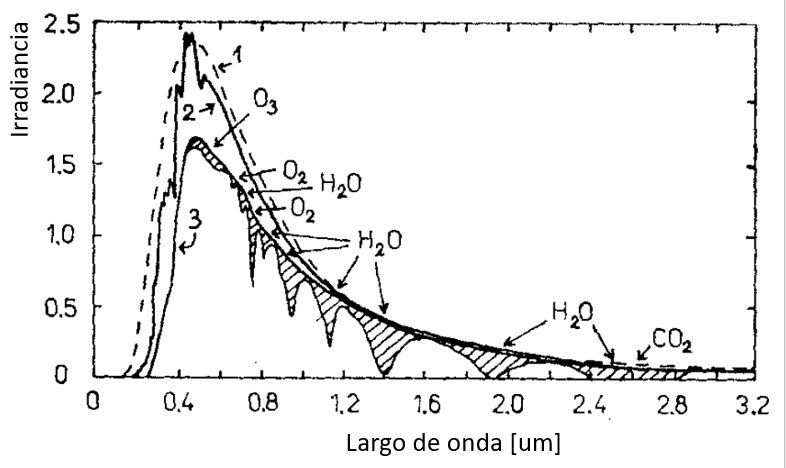
Cuando parte de la luz incidente en la Tierra es absorbida, se generan reducciones en la intensidad del espectro luminoso observado. Esto ocurre debido a que ciertos componentes de la luz, como determinadas longitudes de onda, son absorbidos por los materiales presentes en la atmósfera o en la superficie terrestre. Como resultado, se pueden observar caídas en la intensidad de la luz en diferentes partes del espectro electromagnético.
Este fenómeno de absorción de la luz es importante en diversos campos, como la física atmosférica, la fotografía, la biología y la química. La absorción selectiva de ciertas longitudes de onda puede influir en el clima, los procesos fotosintéticos de las plantas y en la identificación de sustancias químicas mediante espectroscopia.
Es importante destacar que las caídas en la intensidad del espectro luminoso pueden proporcionar información valiosa sobre la composición de la atmósfera y la superficie terrestre, permitiendo estudiar y comprender mejor los procesos físicos y químicos que tienen lugar en nuestro entorno.
ID:(12468, 0)
Efecto de turbulencias en la atmósfera
Descripción 
Si hay turbulencias en la atmósfera, la cantidad de nubes presentes varía, lo que a su vez afecta el número de moléculas de agua y, por consiguiente, la absorción de luz. Dado que esto no depende de la frecuencia, solo se modificará la intensidad del haz de luz y no su frecuencia. Por lo tanto, se puede generar una situación similar a la que se muestra en la imagen:
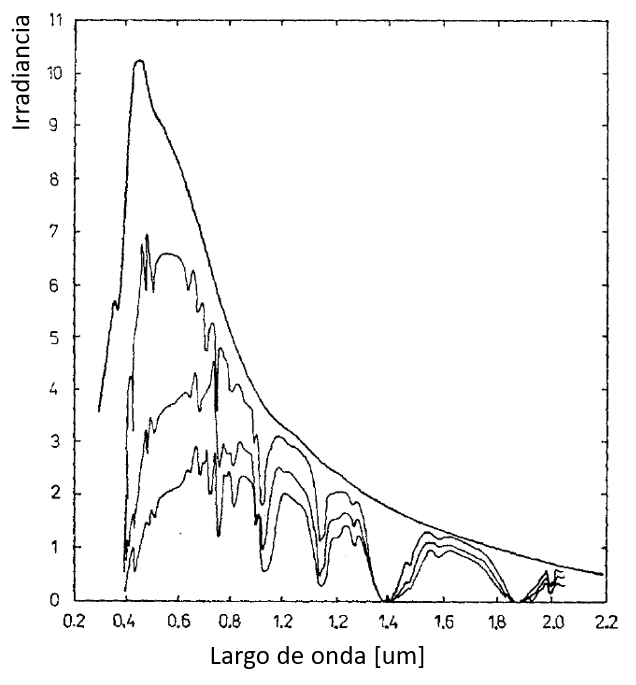
Cuando hay turbulencias atmosféricas, se produce un efecto en la propagación de la luz, lo que resulta en variaciones en la cantidad de nubes y, por ende, en la cantidad de moléculas de agua presentes en la atmósfera. Esto puede dar lugar a una mayor o menor absorción de la luz en diferentes regiones del espectro electromagnético. La imagen muestra cómo la intensidad de la luz puede fluctuar debido a las turbulencias atmosféricas, lo que crea variaciones en la apariencia y brillo del haz de luz.
Es importante tener en cuenta que la turbulencia atmosférica y sus efectos en la propagación de la luz pueden tener impactos significativos en la calidad de las observaciones astronómicas, la fotografía y otros campos que dependen de una iluminación estable y uniforme.
ID:(12469, 0)
Flujo radiante
Ecuación 
Para modelar el flujo de radiación, se puede comenzar describiendo la energía radiativa emitida por unidad de tiempo. Por lo tanto, se define mediante:
El flujo de radiación es la cantidad de energía radiativa que atraviesa una superficie por unidad de tiempo. Se expresa típicamente en vatios por metro cuadrado (W/m²). Esta medida es fundamental para comprender y estudiar la transferencia de energía radiativa en diversos fenómenos, como el calentamiento solar, la radiación térmica y la propagación de ondas electromagnéticas.
ID:(12471, 0)
Flujo radiante por elemento de ángulo
Descripción 
Si el flujo radiante depende de la dirección, tiene sentido calcular su contribución en un elemento de ángulo definido. Por lo tanto, es necesario introducir el concepto de un elemento de ángulo que, al abarcar todas las direcciones, debe dar como resultado 4\pi, que es el elemento de ángulo de una esfera. Por lo general, se denota como d\Omega y corresponde a un tipo de cono, como se muestra en el diagrama a continuación:
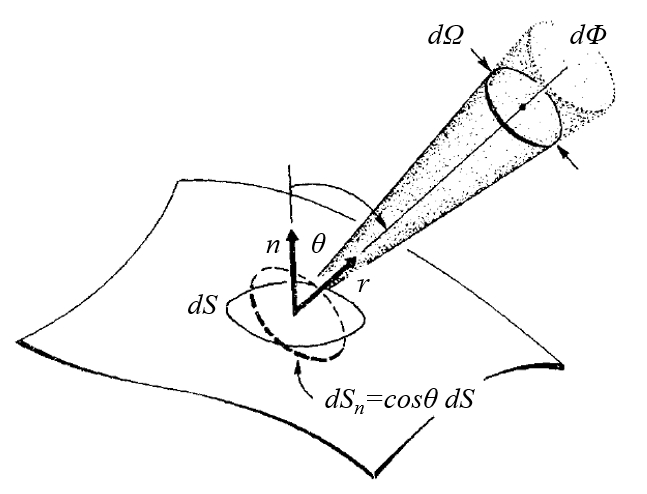
Este diagrama ilustra cómo se define el elemento de ángulo d\Omega. Representa una región en el espacio que abarca un cono infinitesimal con su vértice en el punto de interés. La magnitud del elemento de ángulo d\Omega depende del tamaño del cono y puede variar según la geometría del sistema.
ID:(12476, 0)
Flujo radiante angular
Ecuación 
Si se determina la fracción del flujo de radiación irradiado en un elemento de ángulo, se puede definir la densidad angular del flujo radiante utilizando la siguiente expresión:
| \Phi = \displaystyle\frac{d Q_e }{d t } |
Esta ecuación representa la fracción del flujo de radiación que atraviesa el elemento de ángulo en relación al flujo total. La densidad angular del flujo radiante se obtiene al dividir esta fracción por el elemento de ángulo diferencial d\Omega.
La densidad angular del flujo radiante proporciona información sobre la distribución espacial y direccional de la radiación en un sistema. Es una medida importante para comprender cómo la energía radiante se propaga y se distribuye en diferentes direcciones.
ID:(12472, 0)
Elemento de ángulo
Descripción 
En forma gráfica, el elemento de ángulo en coordenadas se construye mediante un arco del ángulo azimutal y otro arco del ángulo polar multiplicado por el seno de este último.
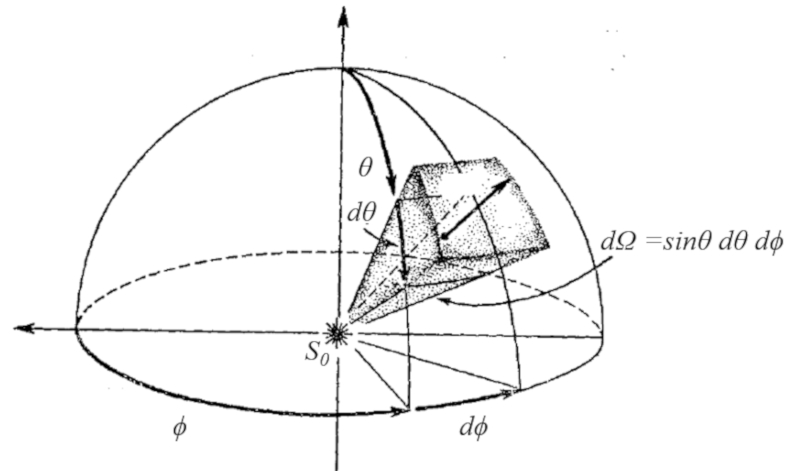
La representación gráfica de un elemento de ángulo en coordenadas es esencial para visualizar y comprender cómo se extiende en el espacio. Consiste en trazar un arco en el plano horizontal, correspondiente al ángulo azimutal, y otro arco en el plano vertical, correspondiente al ángulo polar. El tamaño del arco del ángulo polar se multiplica por el seno de ese ángulo para tener en cuenta la proyección en el plano horizontal.
ID:(12475, 0)
Elemento de ángulo
Ecuación 
Si se trabaja en coordenadas esféricas, el elemento de ángulo se puede calcular utilizando un segmento del ángulo polar \phi y el ángulo azimutal \theta. El elemento de ángulo sólido se obtiene mediante esta construcción gráfica
ID:(12474, 0)
Radiancia
Ecuación 
Con la densidad angular del flujo radiante, definida con elemento de angulo solido rad^2, elemento de flujo radiante W y flujo radiante angular W/rad^2 como
| I = \displaystyle\frac{ d\Phi }{ d\Omega } |
se puede definir la radiancia como la fracción de la densidad angular del flujo por elemento superficie con elemento de angulo solido rad^2, elemento de flujo radiante W y flujo radiante angular W/rad^2 como
| L = \displaystyle\frac{ dI }{ dS } |
ID:(12473, 0)
Ley de Lambert
Ecuación 
Si la presencia del agua es homogénea, sea en forma de vapor o de liquido, se tendrá que la irradiancia se perderá
\displaystyle\frac{dL}{L}\propto dr
Por ello la irradiancia será
A medida que el haz avanza por el medio en una distancia
\displaystyle\frac{dL}{L}
\\n\\nes proprocional al camino recorrido
\displaystyle\frac{dL}{L}\propto dr
\\n\\nSi se introduce la constante de proporcionalidad como
\displaystyle\frac{dL}{L}=-\alpha dr
donde el signo negativo se debe a que la luminosidad se va reduciendo. Por ello la ecuación que rige la luminosidad es una ecuación de primer orden
| \displaystyle\frac{d L }{d r } = - \alpha L |
con
ID:(12470, 0)
Solución de la ley de Lambert
Ecuación 
La ley de Lambert, con coeficiente de absorción 1/m, distancia recorrida m y radiancia W/m^2 rad^2
| \displaystyle\frac{d L }{d r } = - \alpha L |
se puede integrar dando la luminosidad en función de la distancia igual a
La integración de la ecuación diferencial
| \displaystyle\frac{d L }{d r } = - \alpha L |
\\n\\npara una luminosidad
\displaystyle\int_0^{L_0} \displaystyle\frac{dL}{L} = -\displaystyle\int_0^{r}\alpha dr
lo que arroja
| L = L_0 e^{- \alpha r } |
ID:(12477, 0)
Coeficiente de absorción en el infrarrojo (NIR)
Imagen 
Los valores del coeficiente de absorción son mayores en el rango infrarrojo debido en parte a lo que se denomina la sustancia amarilla que corresponde a los restos de vida orgánica. El coeficiente se va reduciendo en dirección de largos de onda mayores que corresponden a el rango visible (VIS):
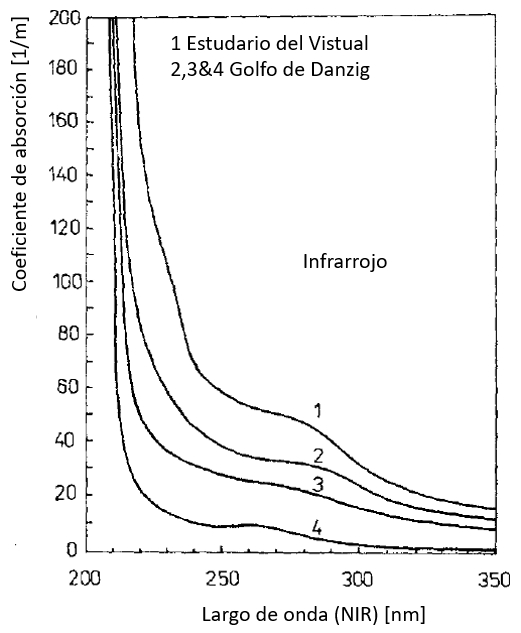
ID:(12478, 0)
Coeficiente de absorción en el rango visible (VIS)
Imagen 
Los valores del coeficiente de absorción en el rango visible (VIS) pasan por un mínimo creciendo para largos de onda mayores:
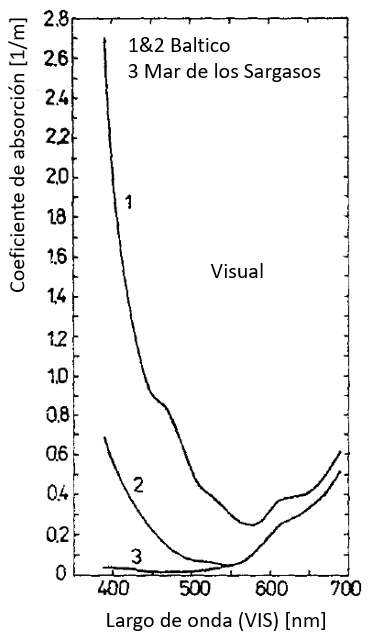
ID:(12479, 0)
Disminución del coeficiente de absorción con la profundidad
Imagen 
Si se compara el coeficiente de absorción a distintas profundidades (o sea distintas presiones) se nota que en general se mantiene la forma pero se va reduciendo con la profundidad:

ID:(12480, 0)
Origen del coeficiente de absorción en función de el largo de onda
Imagen 
Si se analiza el origen del coeficiente de absorción en el rango visible que ve que:
• en los largos de onda menores el efecto de la sustancia amarilla (restos de vida orgánica) domina
• otros materiales en suspensión también tiene una contribución para largos de ondas menores
• el incremento para largo de ondas mayores es propio del agua
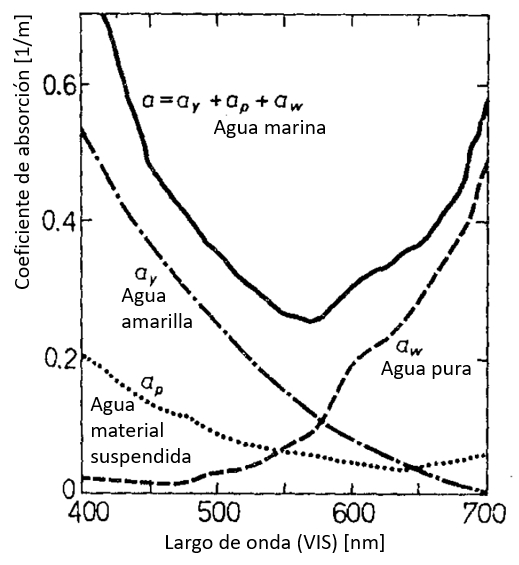
ID:(12481, 0)
