Usuario:
Reflexión de una onda
Imagen 
Cuando una onda llega a una interface entre dos medios en que la velocidad de propagación es distinta se tiene que:
• una parte de la onda es transmitida con una menor amplitud
• una parte de la onda es reflejada no solo teniendo una menor amplitud, ademas pudiendo sufrir un desface
De wikipedia
ID:(12402, 0)
Reflexión con cambio de fase
Imagen
Un pulso que se propaga puede sufrir un cambio de fase en el proceso de reflexión. Si esto ocurre el pulso sufre un cambio de fase en
ID:(12374, 0)
Reflexión sin cambio de fase
Imagen
Un pulso que se propaga puede sufrir un cambio de fase en el proceso de reflexión. Si esto no ocurre el pulso se refleja de la misma forma como incidió:
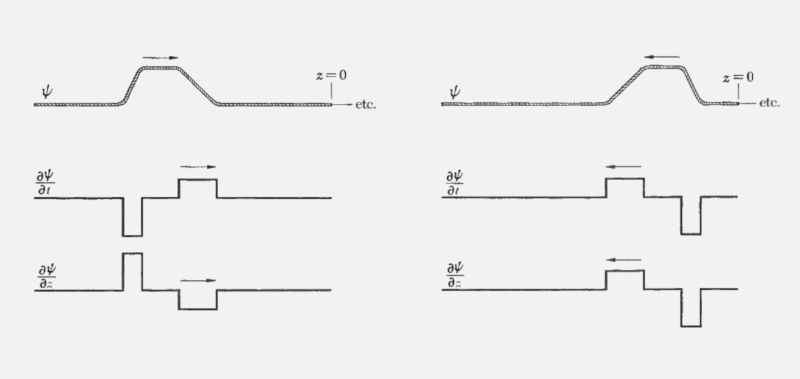
ID:(12375, 0)
Factor de reflexión
Ecuación
Para describir el problema de la reflexión y transmisión se pueden introducir los factores de reflexión y transmisión de modo que en el caso de la reflexión se tiene que con
 $ u_r = R u_i $ |
ID:(12464, 0)
Factor de transmisión
Ecuación
Para describir el problema de la reflexión y transmisión se pueden introducir los factores de reflexión y transmisión de modo que en el caso de la transmisión se tiene que con
| $ u_t = T u_i $ |
ID:(12465, 0)
Relación de reflexión, invariancia de la frecuencia
Ecuación
Si una onda con amplitud
$(u_i + u_r)e^{i\omega_it}=u_te^{i\omega_tt}$
La única forma que esto puede ocurrir para todo tiempo es que ambas frecuencias angulares sean iguales:
Esto es con
| $ \omega_i = \omega_t$ |
En otras palabras una onda no sufre variación en su frecuencia al pasar de un medio a otro.
ID:(12459, 0)
Relación de reflexión, relación de amplitudes
Ecuación
Si la continuidad exige de que las ondas de incidencia, reflexión y transmisión cumplan\\n\\n
$(u_i + u_r)e^{i\omega_it}=u_te^{i\omega_tt}$
y por otro lado las frecuencias angulares son iguales, con frecuencia angular en el medio incidente $rad/s$ y frecuencia angular en el medio transmitido $rad/s$
| $ \omega_i = \omega_t$ |
se tiene que las amplitudes deben satisfacer con frecuencia angular en el medio incidente $rad/s$ y frecuencia angular en el medio transmitido $rad/s$
| $ u_i + u_r = u_t $ |
ID:(12460, 0)
Relación de reflexión, relación de dispersión
Ecuación
Como las frecuencias angulares son iguales y las velocidades en ambos medios son distintas, los vectores de onda deberán ser con
| $ k = \displaystyle\frac{ \omega }{ c }$ |
ID:(12461, 0)
Relación de reflexión, sin quiebres
Ecuación
Si las funciones de onda deben ser 'suabes' o sea no solo continuas, ademas no tener cambios en su pendiente se debe dar que la onda en el lado de incidencia\\n\\n
$u_ie^{ik_1x}+u_re^{-ik_1x}$
\\n\\ndebe tener en el origen la misma pendiente que la transmitida\\n\\n
$u_te^{ik_2x}$
Nota: el signo en el exponente esta determinado por la dirección en que propagan.
Por ello si se derivan ambas ecuaciones, se evalúan en el origen y se igualan se obtiene la segunda condicióncon
| $ k_i ( u_i - u_r ) = k_t u_t $ |
ID:(12462, 0)
Relación de reflexión en función de los vectores de onda
Ecuación
Si se resuelve el sistema de ecuaciones dado por la ecuación para la amplitud, con amplitud incidente $-$, amplitud reflejada $-$ y amplitud transmitida $-$
| $ u_i + u_r = u_t $ |
y la relación con los vectores de onda amplitud incidente $-$, amplitud reflejada $-$, amplitud transmitida $-$, vector de onda en el medio incidente $1/m$ y vector de onda en el medio transmitido $1/m$
| $ k_i ( u_i - u_r ) = k_t u_t $ |
se obtiene con amplitud incidente $-$, amplitud reflejada $-$ y factor de reflexión $-$
| $ u_r = R u_i $ |
con amplitud incidente $-$, amplitud reflejada $-$ y factor de reflexión $-$ la relación
| $ R =\displaystyle\frac{ k_i - k_t }{ k_i + k_t }$ |
ID:(12415, 0)
Relación de transmisión en función de los vectores de onda
Ecuación
Si se resuelve el sistema de ecuaciones dado por la ecuación para la amplitud, con amplitud incidente $-$, amplitud reflejada $-$ y amplitud transmitida $-$
| $ u_i + u_r = u_t $ |
y la relación con los vectores de onda amplitud incidente $-$, amplitud reflejada $-$, amplitud transmitida $-$, vector de onda en el medio incidente $1/m$ y vector de onda en el medio transmitido $1/m$
| $ k_i ( u_i - u_r ) = k_t u_t $ |
se obtiene con amplitud incidente $-$, amplitud transmitida $-$ y factor de transmisión $-$
| $ u_t = T u_i $ |
con amplitud incidente $-$, amplitud transmitida $-$ y factor de transmisión $-$ la relación
| $ T =\displaystyle\frac{2 k_i }{ k_i + k_t }$ |
ID:(12466, 0)
Transmisión
Ecuación
Con la relación de transmisión en función del vector de onda, con factor de transmisión $-$, vector de onda en el medio incidente $1/m$ y vector de onda en el medio transmitido $1/m$
| $ T =\displaystyle\frac{2 k_i }{ k_i + k_t }$ |
la relación de dispersión frecuencia angular $rad/s$, vector de onda $1/m$ y velocidad de la luz $m/s$
| $ k = \displaystyle\frac{ \omega }{ c }$ |
\\n\\ny la impedancia dada por\\n\\n
$Z=\rho c$
se puede generalizar la relación con frecuencia angular $rad/s$, vector de onda $1/m$ y velocidad de la luz $m/s$ como
| $ T = \displaystyle\frac{2 Z_i }{ Z_i + Z_t } $ |
ID:(12387, 0)
Reflexión
Ecuación
Con la relación de reflexión en función del vector de onda, con factor de reflexión $-$, vector de onda en el medio incidente $1/m$ y vector de onda en el medio transmitido $1/m$
| $ R =\displaystyle\frac{ k_i - k_t }{ k_i + k_t }$ |
la relación de dispersión frecuencia angular $rad/s$, vector de onda $1/m$ y velocidad de la luz $m/s$
| $ k = \displaystyle\frac{ \omega }{ c }$ |
\\n\\ny la impedancia dada por\\n\\n
$Z=\rho c$
se puede generalizar la relación con frecuencia angular $rad/s$, vector de onda $1/m$ y velocidad de la luz $m/s$ como
| $ R = \displaystyle\frac{ Z_i - Z_t }{ Z_i + Z_t }$ |
ID:(12386, 0)
Albedo para cielo despejado
Imagen
Cuanta luz penetra en el océano depende de la reflexión que sufra en la superficie. Esta a su vez depende del angulo con que incide la radiación sobre la superficie. El albedo describe la cantidad reflejada y por ello es el complemento de la transmitida. Si se observan los datos para los distintos ángulos se ve que para ángulos menores (puesta y salida del sol) el albedo es mayor significando que menos luz penetra en el océano:
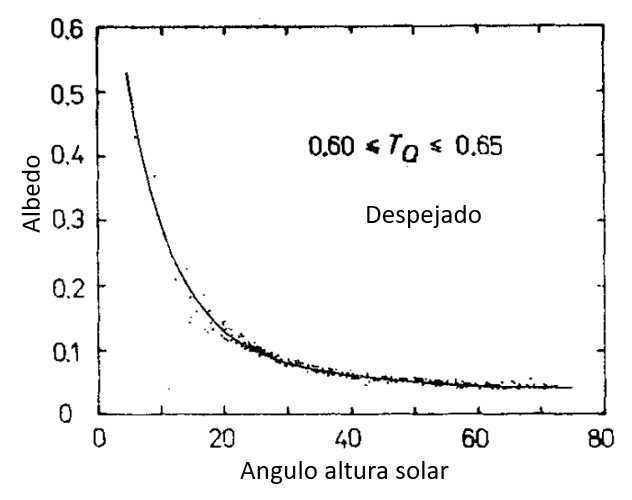
ID:(12491, 0)
Albedo para cielo cubierto
Imagen
Cuando el cielo esta cubierto la mayor parte de la luz es difusa por lo que la influencia de la luz directa del sol decrece y se observa el valor del albedo de ángulos mayores de incidencia para cielo descubierto:
ID:(12492, 0)
Transmisión en función del viento
Imagen
Como el viento afecta el oleaje influencia la condición de la superficie afectando la transmisión de la luz al interior del océano. Esto se observa experimentalmente
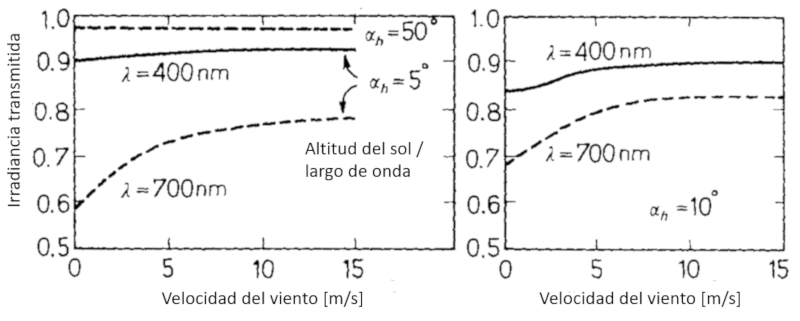
ID:(12493, 0)
Transmisión en función del angulo de incidencia del sol
Imagen
Al igual que la incidencia del sol afecta la reflexión (albedo) lo hace con el complemento que es la transmisión. Esto se observa experimentalmente:
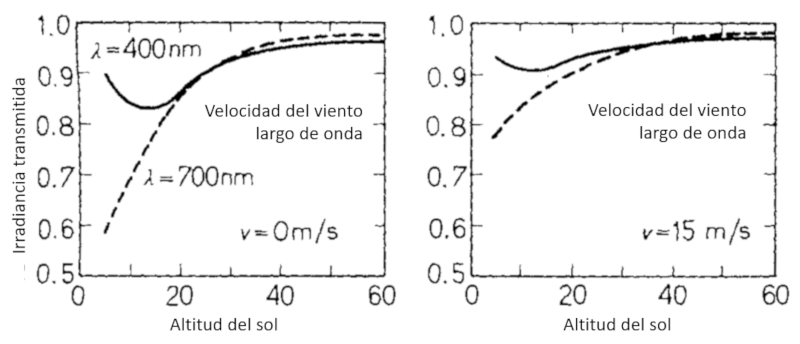
ID:(12494, 0)