Oscillations of water molecules
Description 
Water molecules are capable of oscillating in different modes.
Whenever a light wave with a frequency matching the frequency of the oscillation mode is present, two things occur:
• The molecule's mode is activated.
• The energy required to activate the mode is obtained from the light wave, thereby reducing its intensity.
In other words, when a light wave coincides with the oscillation frequency of a water molecule, that molecule absorbs energy from the light and enters a specific vibrational state. This phenomenon is crucial in various processes related to the interaction of light with water, such as light absorption in the visible spectrum and light scattering in optical phenomena like rainbows.

ID:(12467, 0)
Spectrum of sunlight
Description 
When a portion of the light that reaches the Earth is absorbed, decreases in the intensity of the spectrum can be observed:
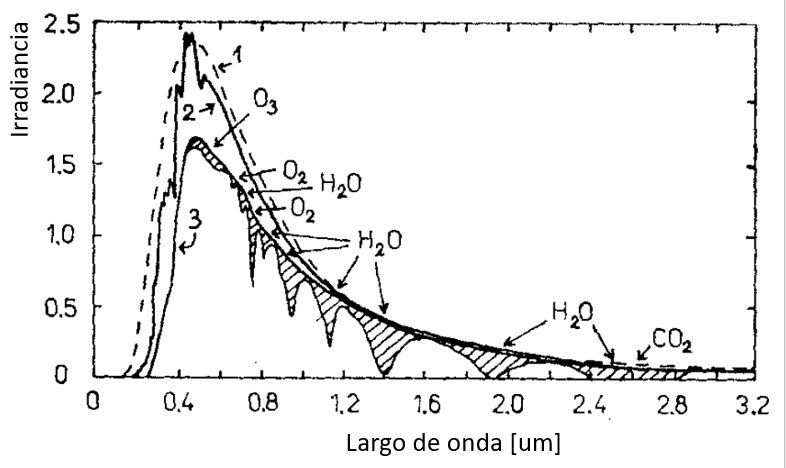
When some of the incident light on Earth is absorbed, reductions in the intensity of the observed light spectrum occur. This happens because certain components of light, such as specific wavelengths, are absorbed by materials present in the atmosphere or on the Earth's surface. As a result, decreases in light intensity can be observed across different parts of the electromagnetic spectrum.
This phenomenon of light absorption is significant in various fields, including atmospheric physics, photography, biology, and chemistry. The selective absorption of certain wavelengths can influence climate, plant photosynthetic processes, and the identification of chemical substances through spectroscopy.
It is important to note that the decreases in light intensity within the spectrum can provide valuable information about the composition of the atmosphere and Earth's surface, allowing for a better understanding and study of the physical and chemical processes occurring in our environment.
ID:(12468, 0)
Effect of turbulence in the atmosphere
Description 
If there are turbulences in the atmosphere, the quantity of clouds present will vary, which in turn affects the number of water molecules and their absorption of light. Since this does not depend on frequency, only the intensity of the beam will be modified, not its frequency. Therefore, a situation like the one shown in the image can arise:
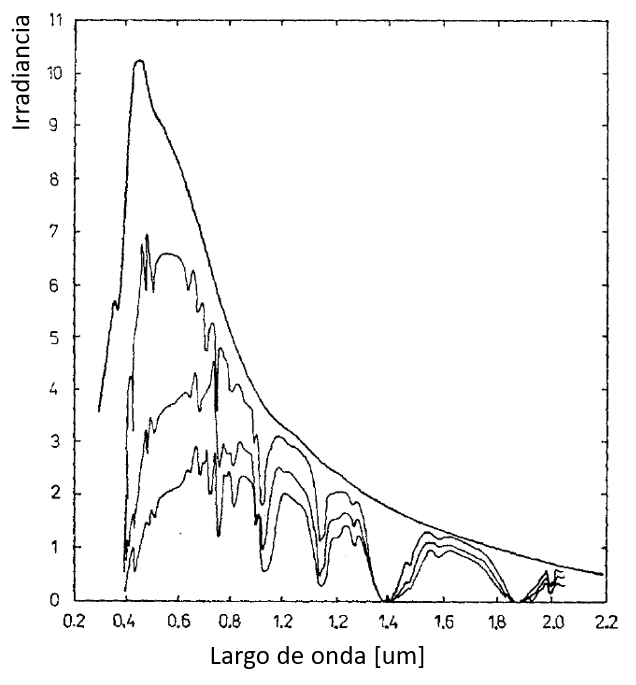
When atmospheric turbulence occurs, it affects the propagation of light, resulting in fluctuations in the quantity of clouds and, consequently, the number of water molecules in the atmosphere. This can lead to greater or lesser absorption of light across different regions of the electromagnetic spectrum. The image illustrates how the intensity of light can fluctuate due to atmospheric turbulence, creating variations in the appearance and brightness of the light beam.
It is important to note that atmospheric turbulence and its effects on light propagation can have significant impacts on the quality of astronomical observations, photography, and other fields that rely on stable and uniform illumination.
ID:(12469, 0)
Radiant flow
Equation 
To model the radiation flow, one can start by describing the radiative energy emitted per unit time. Therefore, it is defined as follows:
Radiation flow is the amount of radiative energy that passes through a surface per unit time. It is typically expressed in watts per square meter (W/m²). This measure is fundamental for understanding and studying the transfer of radiative energy in various phenomena, such as solar heating, thermal radiation, and the propagation of electromagnetic waves.
ID:(12471, 0)
Radiant flux per angle element
Description 
If radiant flux depends on direction, it makes sense to calculate its contribution within a defined angle element. Therefore, it is necessary to introduce the concept of an angle element that, when encompassing all directions, should result in $4\pi$, which is the solid angle of a sphere. It is commonly denoted as $d\Omega$ and corresponds to a type of cone, as shown in the diagram below:
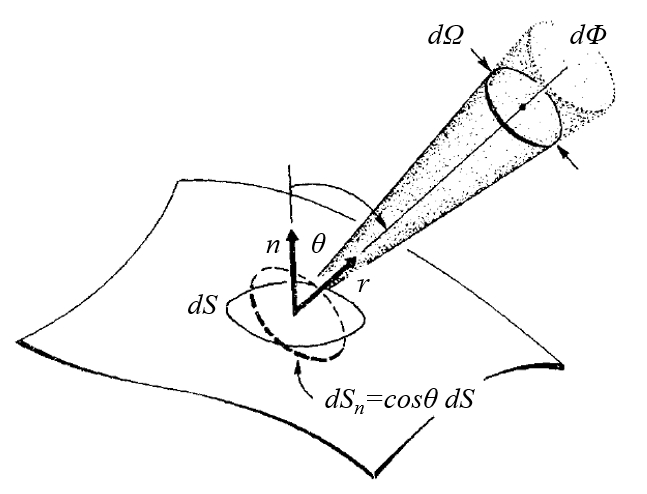
This diagram illustrates how the angle element $d\Omega$ is defined. It represents a region in space that encompasses an infinitesimal cone with its vertex at the point of interest. The magnitude of the angle element $d\Omega$ depends on the size of the cone and can vary depending on the system's geometry.
ID:(12476, 0)
Angular radiant flux
Equation 
If the fraction of radiation flux irradiated in an angular element is determined, the angular density of radiant flux can be defined using the following expression:
| $ \Phi = \displaystyle\frac{d Q_e }{d t }$ |
This equation represents the fraction of radiation flux that passes through the angular element relative to the total flux. The angular density of radiant flux is obtained by dividing this fraction by the differential angle element $d\Omega$.
The angular density of radiant flux provides information about the spatial and directional distribution of radiation in a system. It is an important measure for understanding how radiant energy propagates and is distributed in different directions.
ID:(12472, 0)
Angle element
Description 
In graphical form, the angle element in coordinates is constructed by an arc of the azimuthal angle and another arc of the polar angle multiplied by the sine of the latter.
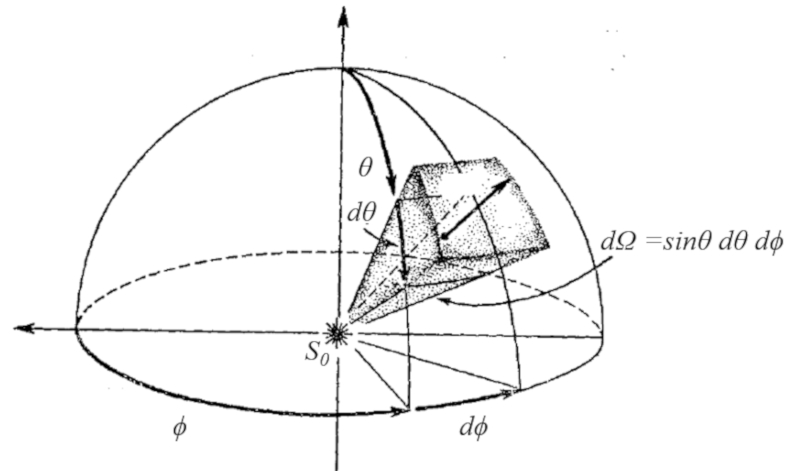
The graphical representation of an angle element in coordinates is essential for visualizing and understanding how it extends in space. It involves drawing an arc in the horizontal plane, corresponding to the azimuthal angle, and another arc in the vertical plane, corresponding to the polar angle. The size of the arc of the polar angle is multiplied by the sine of that angle to take into account the projection in the horizontal plane.
ID:(12475, 0)
Angle element
Equation 
If working in spherical coordinates, the angle element can be calculated based on a segment of the polar angle $\phi$ and the azimuthal angle $\theta$. The solid angle element is obtained through this graphical construction.
ID:(12474, 0)
Radiancia
Equation 
Con la densidad angular del flujo radiante, definida con elemento de angulo solido $rad^2$, elemento de flujo radiante $W$ and flujo radiante angular $W/rad^2$ como
| $ I = \displaystyle\frac{ d\Phi }{ d\Omega }$ |
se puede definir la radiancia como la fracción de la densidad angular del flujo por elemento superficie con elemento de angulo solido $rad^2$, elemento de flujo radiante $W$ and flujo radiante angular $W/rad^2$ como
| $ L = \displaystyle\frac{ dI }{ dS }$ |
ID:(12473, 0)
Ley de Lambert
Equation 
Si la presencia del agua es homogénea, sea en forma de vapor o de liquido, se tendrá que la irradiancia se perderá
$\displaystyle\frac{dL}{L}\propto dr$
Por ello la irradiancia será
A medida que el haz avanza por el medio en una distancia
$\displaystyle\frac{dL}{L}$
\\n\\nes proprocional al camino recorrido
$\displaystyle\frac{dL}{L}\propto dr$
\\n\\nSi se introduce la constante de proporcionalidad como
$\displaystyle\frac{dL}{L}=-\alpha dr$
donde el signo negativo se debe a que la luminosidad se va reduciendo. Por ello la ecuación que rige la luminosidad es una ecuación de primer orden
| $ \displaystyle\frac{d L }{d r } = - \alpha L $ |
con
ID:(12470, 0)
Solución de la ley de Lambert
Equation 
La ley de Lambert, con coeficiente de absorción $1/m$, distancia recorrida $m$ and radiancia $W/m^2 rad^2$
| $ \displaystyle\frac{d L }{d r } = - \alpha L $ |
se puede integrar dando la luminosidad en función de la distancia igual a
La integración de la ecuación diferencial
| $ \displaystyle\frac{d L }{d r } = - \alpha L $ |
\\n\\npara una luminosidad
$\displaystyle\int_0^{L_0} \displaystyle\frac{dL}{L} = -\displaystyle\int_0^{r}\alpha dr$
lo que arroja
| $ L = L_0 e^{- \alpha r } $ |
ID:(12477, 0)
Coeficiente de absorción en el infrarrojo (NIR)
Image 
Los valores del coeficiente de absorción son mayores en el rango infrarrojo debido en parte a lo que se denomina la sustancia amarilla que corresponde a los restos de vida orgánica. El coeficiente se va reduciendo en dirección de largos de onda mayores que corresponden a el rango visible (VIS):
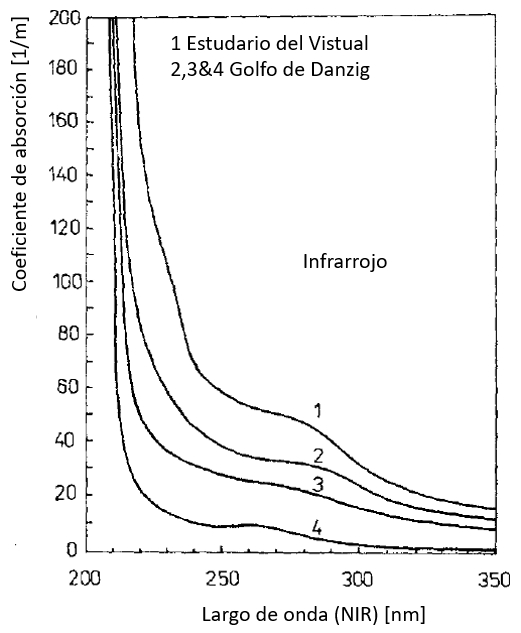
ID:(12478, 0)
Coeficiente de absorción en el rango visible (VIS)
Image 
Los valores del coeficiente de absorción en el rango visible (VIS) pasan por un mínimo creciendo para largos de onda mayores:
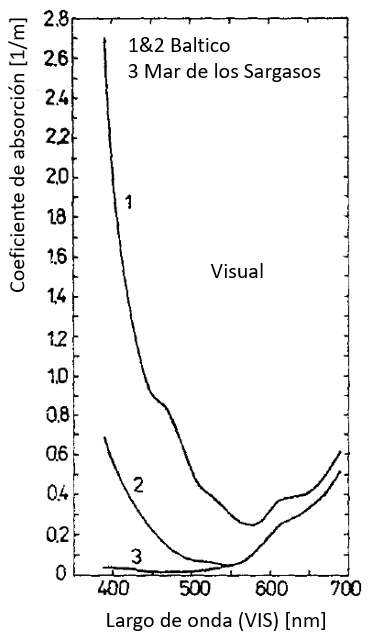
ID:(12479, 0)
Disminución del coeficiente de absorción con la profundidad
Image 
Si se compara el coeficiente de absorción a distintas profundidades (o sea distintas presiones) se nota que en general se mantiene la forma pero se va reduciendo con la profundidad:

ID:(12480, 0)
Origen del coeficiente de absorción en función de el largo de onda
Image 
Si se analiza el origen del coeficiente de absorción en el rango visible que ve que:
• en los largos de onda menores el efecto de la sustancia amarilla (restos de vida orgánica) domina
• otros materiales en suspensión también tiene una contribución para largos de ondas menores
• el incremento para largo de ondas mayores es propio del agua
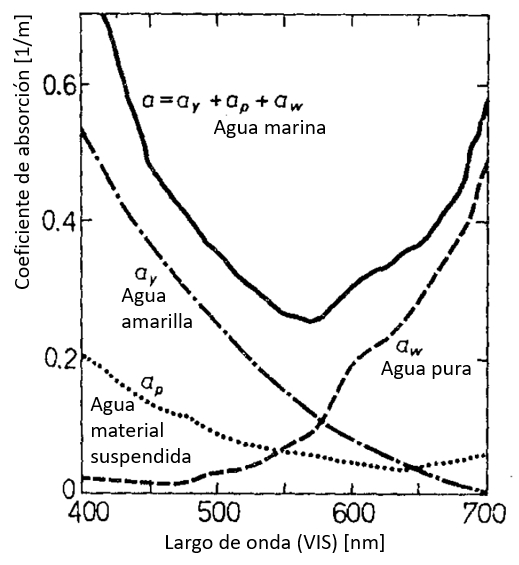
ID:(12481, 0)
