User:
La refracción
Image 
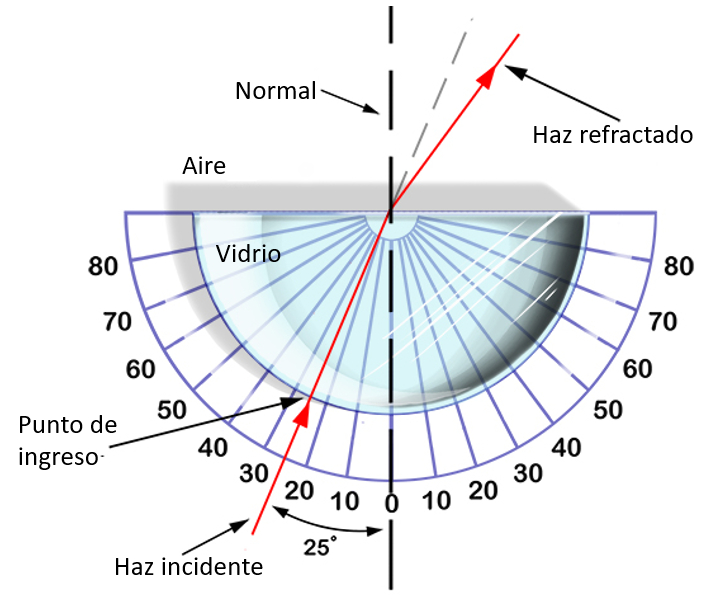
Si un haz pasa de un medio a otro en que la velocidad de propagación es distinta se observa un desvío del haz. Es dice que el haz fue refractado.
ID:(12448, 0)
Comparación mecánica, la desigualdad de terreno desvía
Image
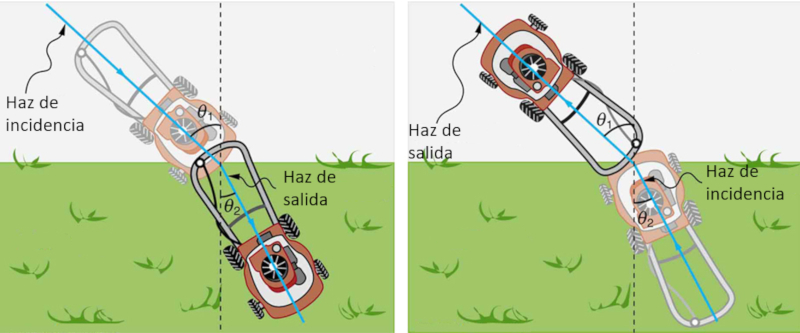
Si un vehículo sufre mas resistencia en una de sus ruedas tendera a desviarse hacia aquel lado:
ID:(12441, 0)
Propagación por la curva
Image
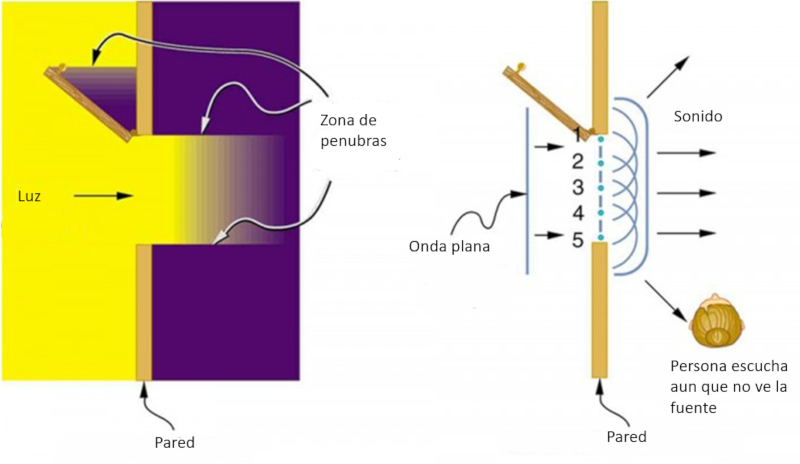
Uno de los fenómenos curiosos de las ondas es que son capaces de propagar detrás de un objeto. Dependiendo del tamaño del largo de la onda el objeto afecta o no a la onda: si es mas pequeña tendera a crear sombras mientras si es mas grande incurrirá en la zona detrás.
ID:(12440, 0)
Principio de Huygens
Image
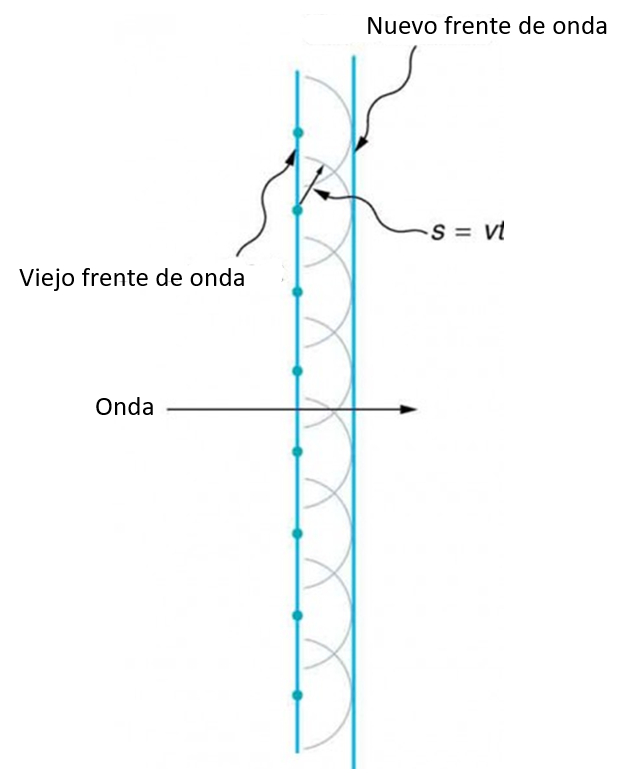
Un nuevo frente de onda se puede armar en función de sumar múltiples fuentes que emiten en forma esférica.
ID:(12442, 0)
Principio de Huygens y reflexión
Image
Para el caso de la reflexión se puede trabajar con el principio de Huygens. Para ello se localizan en forma equidistantes fuentes que son activadas a medida que la onda incidente las alcanza generándose el nuevo frente de onda que tiene el mismo angulo de reflexión que aquel con que incidió:
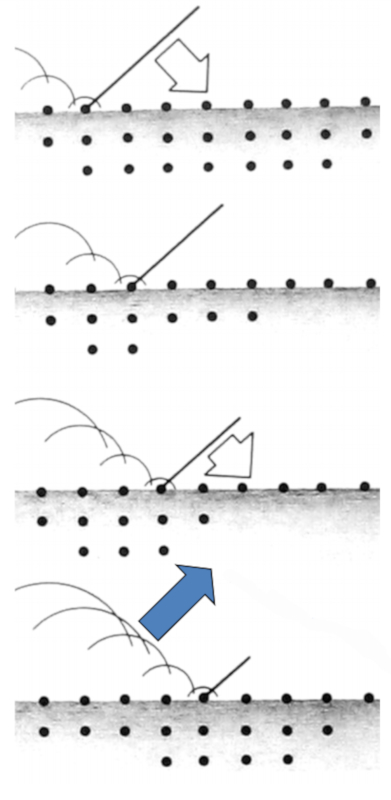
ID:(12458, 0)
Principio de Huygens
Image
Huygens postula que todo frente de ondas se puede construir si se asume que el anterior es una cadena de fuentes que emiten esfericamente. El nuevo frente se genera por simple adición constructiva mientras que las restantes superposiciones se interfieren destructivamente:
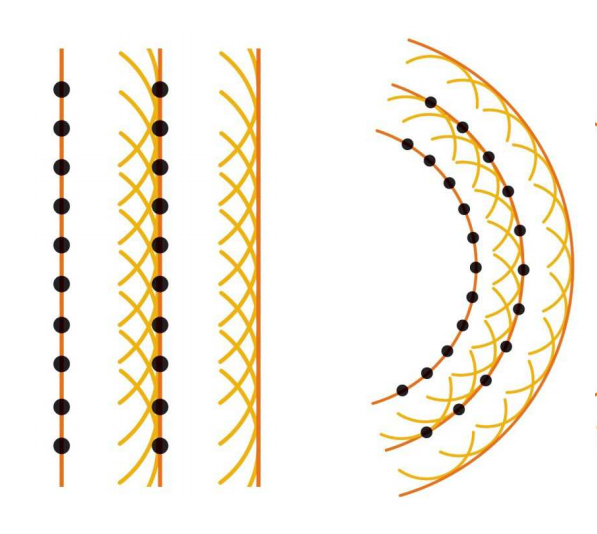
ID:(12457, 0)
Aplicando el principio de Huygens al proceso de refracción
Image
Ante una interface que separa medios de distinta velocidad de propagación se puede construir el nuevo frente con el principio de Huygens. De este se observa que se cumple una relación entre el angulo de incidencia y el de salida en función de la velocidad de la señal en cada medio:
ID:(12444, 0)
Ecuación de Snell
Equation
En base a la trigonometria se observa que:
• el angulo de incidencia es $\theta_1$
&bull: el angulo de salida es $\theta_2$
• si en el primer medio la velocidad es $c_1$ el cateto opuesto al angulo $\theta_1$ sera $c_1\Delta t$ con $\Delta t$ el tiempo transcurrido
• si en el segundo medio la velocidad es $c_2$ el cateto opuesto al angulo $\theta_2$ sera $c_2\Delta t$ con $\Delta t$ el tiempo transcurrido
• la hipotenusa es común e igual por ambas partes.
Calculando con los datos la hipotenusa e igualando estos se obtiene que se tiene
 $\displaystyle\frac{ c_1 }{\sin \theta_1 }=\displaystyle\frac{ c_2 }{\sin \theta_2 }$ |
ID:(12445, 0)
Refracción total
Image
Para el caso de que el haz viaje del medio mas lento al mas rápido se puede dar que no exista un angulo de salida para el angulo de incidencia que se escoja. En este caso ocurre lo que e llama la refracción total, es decir el haz es totalmente reflejado con un angulo de salida igual al de incidencia.
ID:(12446, 0)
Indice de refracción del agua marina en función del largo de onda
Image
El indice de refracción, que se asocia a la velocidad de la luz en el medio respectivo, varia según el largo de onda en el agua marina:
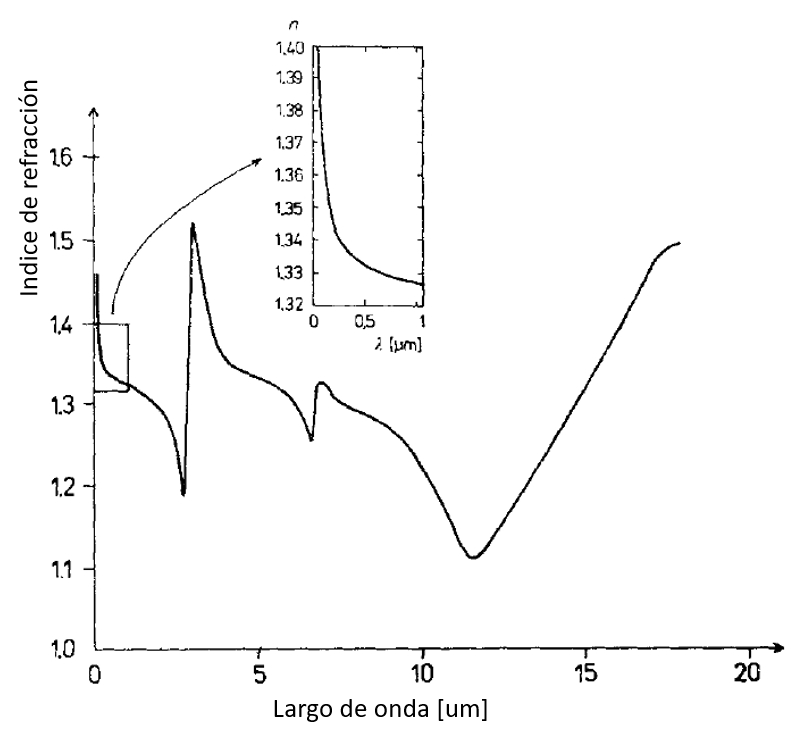
ID:(12490, 0)
Refraction Index
Equation
The refractive index, denoted as $n$, is defined as the ratio of the speed of light in a vacuum, denoted as $c$, to the speed of light in the medium, denoted as $c_m$:
| $ n =\displaystyle\frac{ c }{ v }$ |
ID:(3192, 0)
Frequency and Wavelength of Photon
Equation
The photon is described as a wave, and the photon frequency ($\nu$) is related to ($$) through the speed of Light ($c$), according to the following formula:
| $ c = \nu \lambda $ |
Given that the photon frequency ($\nu$) is the inverse of the period ($T$):
$\nu=\displaystyle\frac{1}{T}$
this means that the speed of Light ($c$) is equal to the distance traveled in one oscillation, which is ($$), divided by the elapsed time, which corresponds to the period:
$c=\displaystyle\frac{\lambda}{T}$
In other words, the following relationship holds:
| $ c = \nu \lambda $ |
This formula corresponds to the mechanical relationship that states the wave speed is equal to the wavelength (distance traveled) divided by the oscillation period, or inversely proportional to the frequency (the inverse of the period).
ID:(3953, 0)