Usuario:


Cosecha de heno y forraje
Storyboard

>Modelo

ID:(1686, 0)


Cosechar forraje
Imagen

>Top



ID:(12843, 0)


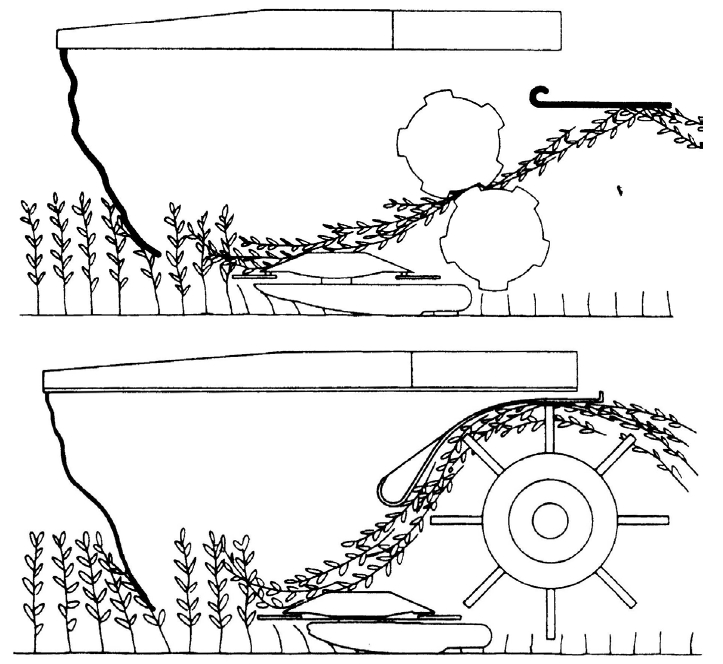
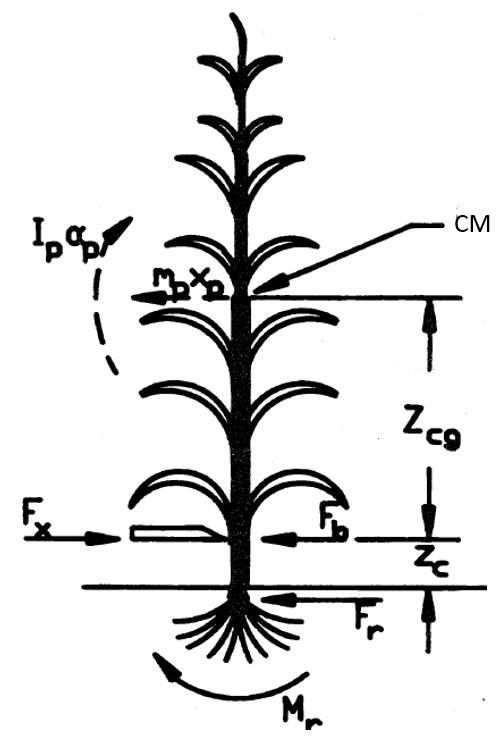
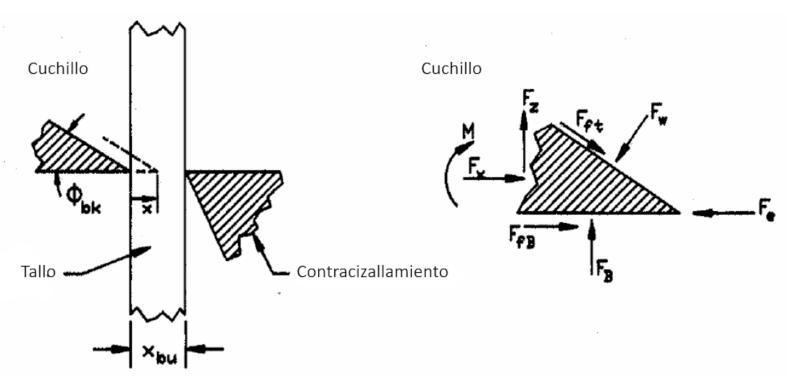
Geometría de corte
Imagen

>Top


La clave esta en el rango del angulo de modo de que el roce evite que se deslice y se pueda cortar

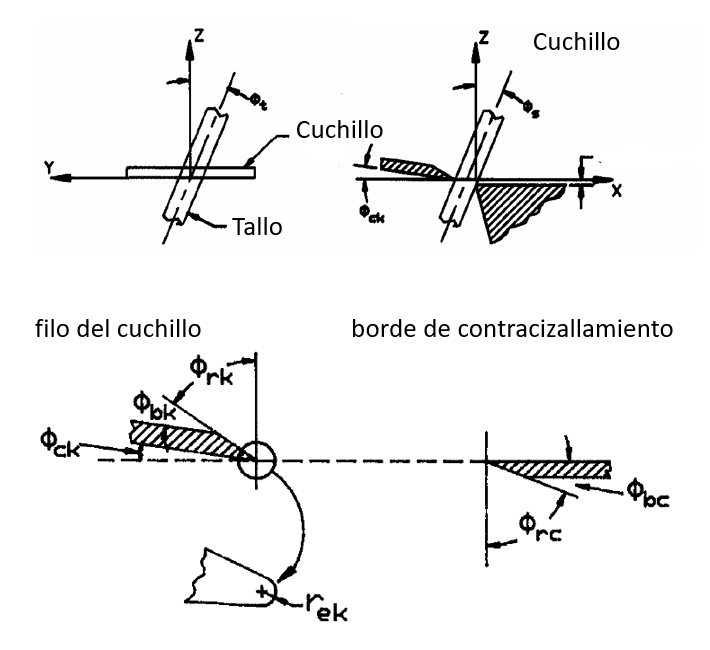
ID:(12844, 0)


Angulo de corte
Ecuación

>Top, >Modelo


El angulo de corte se define en base a los ángulos del cuchillo y del elemento de soporte

$ \phi_{cl} = \phi_{ok} + \phi_{oc} $

ID:(12845, 0)


Máximo angulo oblicuo del cuchillo
Ecuación

>Top, >Modelo


Para que exista deslizamiento de la planta el angulo oblicuo del cuchillo debe ser mayor a

$ \phi_{ok,max} = \arctan f_{ek} $

donde f_{ek} es el indice de roce del cuchillo.

ID:(12846, 0)


Máximo angulo de corte
Ecuación

>Top, >Modelo


Para que exista deslizamiento de la planta el angulo de corte tiene que ser mayor a

$ \phi_{cl,max} = \arctan\displaystyle\frac{ f_{ek} + f_{ec} }{1 - f_{ek} f_{ec} } $

donde f_{ek} y f_{ec} son los indice de roce del cuchillo y del borde de contracizallamiento.

valores típicos son del primero en torno a 0.306 y del segundo en 0.364.

ID:(12847, 0)


Fuerza de quiebre del tallo
Ecuación

>Top, >Modelo


La fuerza F_{bu} necearía para quebrar un tallo se calcula de

$ F_{bu} =\displaystyle\frac{ I S_u }{ c L }$

donde I es el momento de inercia, S_u la tensión critica de la fibra de la planta, c el radio desde el interior a la superficie que soporta fuerza y L el largo entre punto de soporte de la planta a punto de ataque de la fuerza.

.

ID:(12848, 0)


Deflección radial en el corte
Ecuación

>Top, >Modelo


La deflección radial \delta_r es

$ \delta_r =\displaystyle\frac{ F_r L^3 }{ C_b E I }$

donde F_r es la fuerza radial, E el modulo de elasticidad y C una constante según el apoyo.

ID:(12849, 0)


Momento de inercia de una planta solida
Ecuación

>Top, >Modelo


En caso de que la planta es un cilindro solido (no hueco) el momento de inercia I será

$ I =\displaystyle\frac{ \pi d ^4 }{64}$

donde d es el diámetro.

ID:(12850, 0)


Momento de inercia de una planta con centro hueco
Ecuación

>Top, >Modelo


En caso de que la planta es un cilindro hueco el momento de inercia I será

$ I =\displaystyle\frac{ 3\pi d ^3 t }{32}$

donde d es el diámetro y d el ancho de la pared.

ID:(12851, 0)


Dinámica del corte
Imagen

>Top



ID:(12855, 0)


Fuerzas de corte
Imagen

>Top



ID:(12859, 0)


Fuerza de corte del cuchillo
Ecuación

>Top, >Modelo


La fuerza en x de corte del cuchillo F_x es

$ F_x = F_{ek} + \displaystyle\frac{ w B_f x ^{ \lambda }}{ 2 X_{bu} }(\tan \phi_{bk} + 2 f )$

con F_{ek} del tallo sobre lel cuchillo, w el ancho del cuchillo, el módulo volumétrico del forraje B_f, el desplazamiento del cuchillo tras contacto inicial x, un exponente (tipicamente 2) \lambda, la profundidad no comprimida del material entre cuchillo y contracizallamiento X_{bc}, ángulo de bisel del cuchillo \phi_{bk} y el coeficente de fracción del cuchillo f.

ID:(12852, 0)


Area frontal del cuchillo
Ecuación

>Top, >Modelo


El área frontal del cuchillo por ancho A_{ek} es

$ A_{ek} = r_{ek} (1 + cos( \phi_{bk} + \phi_{ck} ))$

con r_{ek} el radio de filo del cuchillo.

ID:(12853, 0)


Potencia de corte
Ecuación

>Top, >Modelo


La potencia de corte P_{cut} es

$ P_{cut} = C_f F_{max} X_{bu} f_{cut}$

con la fuerza media de corte C_f, la fuerza máxima de corte F_{max}, la frecuencia de corte f_{cut} y la profundidad de corte inicial X_{bu}.

ID:(12854, 0)


Ecuación de movimiento de la planta
Ecuación

>Top, >Modelo


En base a la fuerza aplicada por el cuchillo y la oposición de la planta se obtiene la ecuación que permite calcular la rotación de la planta

$I_p \alpha_p = (F_x - F_b)z_{cg}$

en onde I_p es el momenti de inercia, \alpha la aceleración angular y z_{cg} la distancia entre centro de masa y punto de impacto del cuchillo.

ID:(12856, 0)


Velocidad mínima de corte
Ecuación

>Top, >Modelo


Con la aceleración angular se puede calcular la velocidad mínima de impacto del cuchillo sobre la planta

$v_k =\sqrt{d_s\displaystyle\frac{(F_x-F_b)}{m_p}\left(1 +\displaystyle\frac{z_{cg}^2}{r_g^2}\right)} $

ID:(12857, 0)