Usuario:
Bases de clima y su fluctuación
Storyboard 
Las fluctuaciones de la órbita terrestre tienen un efecto directo sobre el balance radiatorio y con ello el clima de la tierra.
ID:(538, 0)
Marte: un ejemplo de planeta con escasa atmósfera
Descripción
En primera aproximación, Marte puede considerarse sin atmósfera, lo que permite un modelo relativamente simple:
Marte
ID:(3070, 0)
Equilibrio de radiación en planeta sin atmósfera
Descripción
En el caso de un planeta sin atmósfera, hay una fracción de la radiación incidente $I_p$ que se refleja como $a_{
u}I_p$, otra fracción se absorbe como $(1-a_{
u})I_p$, y una fracción de la radiación infrarroja $\sigma\epsilon T_e^4$ se irradia:
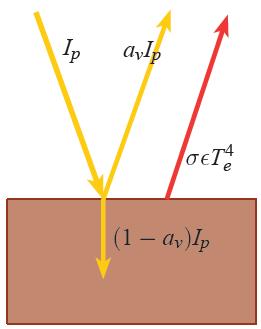
Equilibrio en un planeta sin atmósfera
ID:(3069, 0)
Temperatura de un planeta sin atmósfera (0D)
Ecuación
La energía absorbida por el planeta corresponde a la radiación no reflejada, es decir,
$(1-a_v)I_s$
Esta energía calienta el planeta a una temperatura $T_p$. Este calentamiento resulta en radiación infrarroja, que según la ley de Stefan-Boltzmann se calcula como
$\sigma\epsilon T_p^4$
donde $\sigma$ es la constante de Stefan-Boltzmann y $\epsilon$ es la emisividad.
En un estado de equilibrio, ambas energías son iguales,
$(1-a_v)I_s=\sigma\epsilon T_p^4$
lo que permite obtener una temperatura $T_p$ mediante la siguiente ecuación:
 $ T_p =\left(\displaystyle\frac{(1- a_v ) I_s }{ \sigma \epsilon }\right)^{1/4}$ |
Si utilizamos esta ecuación para estimar la temperatura de diferentes planetas, se obtienen los siguientes datos:
Planeta | Intensidad [W/m^2] | Albedo [-] | Temperatura [C] | Rango [C]
:----------|:---------------------------|:-------------|:----------------------|:--------------:
Mercurio | 9126.49 | 0.088 | 345.83 | -180 a 430
Venus | 2613.78 | 0.76 | 51.17 | 465
Terra | 1367.56 | 0.306 | 86.54 | -89 a 58
Marte | 589.04 | 0.25 | 23.95 | -82 a 0
Júpiter | 50.52 | 0.503 | -128.09 | -150
Saturno | 15.04 | 0.342 | -158.22 | -170
Urano | 3.71 | 0.3 | -190.86 | -200
Netuno | 1.51 | 0.29 | -207.18 | -210
Es notable la desviación, especialmente en los planetas más cercanos al sol, lo cual se debe al efecto de sus respectivas atmósferas.
En este modelo, no se tienen en cuenta las variaciones en la superficie del planeta ni los cambios en la altura de su atmósfera. En ese sentido, el planeta se modela como un punto de dimensión cero (0D).
ID:(4669, 0)
Precesión del eje de la tierra
Descripción
Además de la nutación, el eje de la Tierra experimenta un movimiento giratorio conocido como precesión.
Precisión
La consecuencia de la precesión es que el momento en que experimentamos el verano e invierno va cambiando. Debido a que el período de precesión es de 26,000 años, cada 13,000 años se invierten las estaciones en el tiempo.
ID:(3087, 0)
Intensidad reflejada
Ecuación
Si la intensidad visible del sol es
| $ I_r = a_v I_s $ |
None
ID:(4668, 0)
Precesión de la orbita
Descripción
La intensidad solar fluctúa en función de la precisión de la órbita:
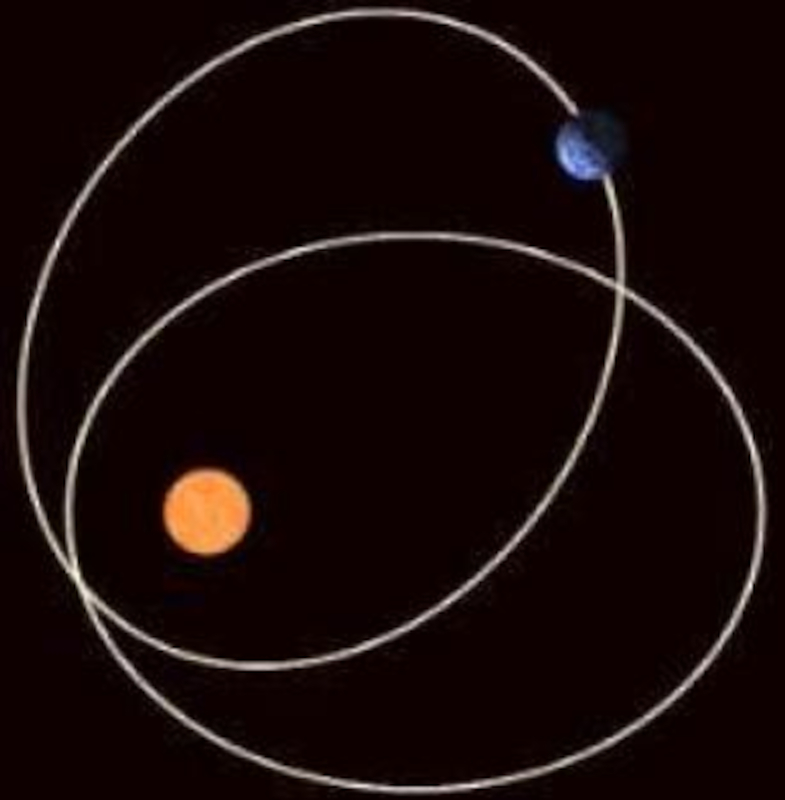
Precisión de la órbita
ID:(3089, 0)
Nutación del eje de la tierra
Descripción
El eje de la Tierra varía en su inclinación entre 22.1 y 24.5 grados. Este proceso se conoce como nutación.
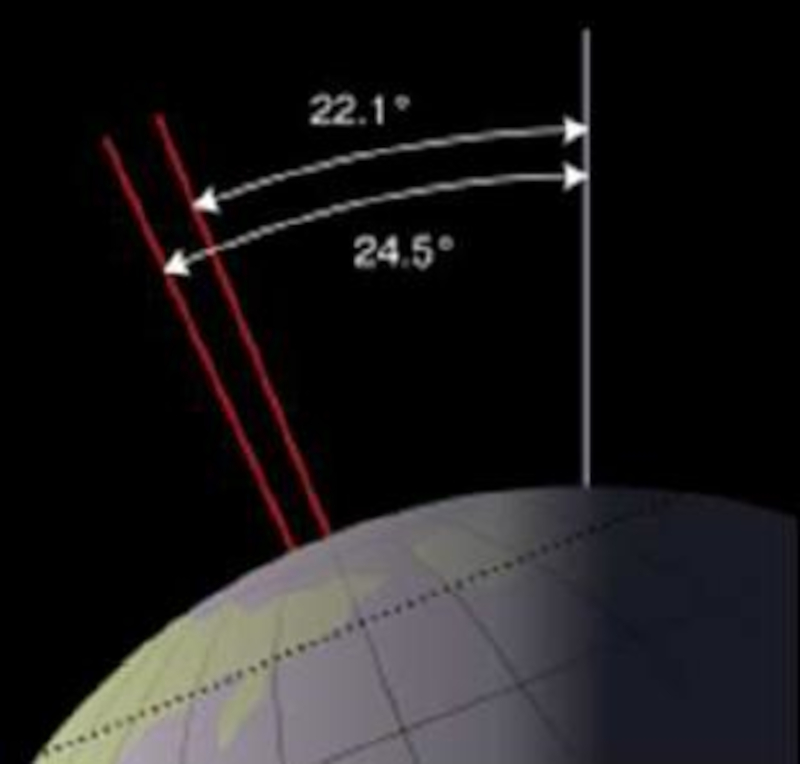
Nutación del eje de la tierra
La nutación se debe a efectos como la influencia de la Luna sobre la Tierra y la forma no perfectamente esférica de nuestro planeta. Cada efecto tiene su propio período característico, siendo el más largo de alrededor de 41,000 años. Se estima que el último valor máximo ocurrió hace aproximadamente 10,700 años (8,700 a.C.), coincidiendo con el final de la última Edad de Hielo.
ID:(3086, 0)
Ciclos de Milankovitch
Descripción
Las fluctuaciones en la orientación del eje y las variaciones en la órbita han llevado a una disminución en la radiación solar en la Tierra, lo que ha resultado en períodos de enfriamiento y en la formación de períodos glaciales.
Ciclos de Milankovitch
La última edad de hielo terminó hace aproximadamente 10.000 años.
ID:(3090, 0)