Storyboard

Die Schwankungen der Erdumlaufbahn wirken sich unmittelbar auf den Strahlungshaushalt und damit auf das Erdklima aus.

>Modell

ID:(538, 0)

Beschreibung

>Top

In einer ersten Annäherung kann davon ausgegangen werden, dass der Mars keine Atmosphäre hat, was eine relativ einfache Modellierung ermöglicht:

ID:(3070, 0)

Beschreibung

>Top

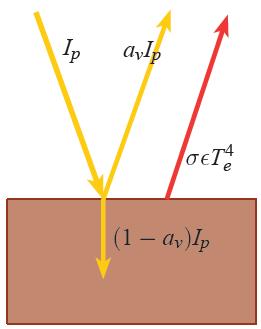
Bei einem Planeten ohne Atmosphäre wird ein Anteil der einfallenden Strahlung $I_p$ als $a_{
u}I_p$ reflektiert, ein weiterer Anteil wird als $(1-a_{
u})I_p$ absorbiert, und ein Anteil der Infrarotstrahlung $\sigma\epsilon T_e^4$ wird abgestrahlt.

ID:(3069, 0)

Gleichung

>Top, >Modell

Der Planet absorbiert und reemittiert die von der Sonne empfangene Strahlung. Die absorbierte Energie des Planeten entspricht der nicht reflektierten Strahlung und kann als

$(1-a_v)I_s$

ausgedrückt werden. Diese Energie erwärmt den Planeten auf eine Temperatur $T_p$. Die resultierende Erwärmung führt zur Infrarotstrahlung, die gemäß dem Stefan-Boltzmann-Gesetz wie folgt beschrieben werden kann:

$\sigma\epsilon T_p^4$

wobei $\sigma$ die Stefan-Boltzmann-Konstante und $\epsilon$ die Emissionsrate ist.

Im Gleichgewichtszustand sind die absorbierte Energie und die emittierte Energie gleich, was durch

$(1-a_v)I_s=\sigma\epsilon T_p^4$

beschrieben wird. Diese Gleichung ermöglicht es uns, die Temperatur $T_p$ des Planeten zu berechnen:

$ T_p =\left(\displaystyle\frac{(1- a_v ) I_s }{ \sigma \epsilon }\right)^{1/4}$

Bedingungen

Variablen

$a_{VIS}$

Albedo Visible (VIS)

$-$

7722

$I_s$

Durchschnittliche Intensität der Erde

$W/m^2$

6502

$\epsilon$

Emissions

$-$

5242

$T_p$

Planet Temperatur

$K$

6505

$\sigma$

Stefan-Boltzmann-Konstante

1.38e-23

$J/m^2K^4s$

5241

Beziehung

Bei Verwendung dieser Gleichung zur Abschätzung der Temperaturen verschiedener Planeten ergeben sich folgende Daten:

Planet | Intensität [W/m^2] | Albedo [-] | Temperatur [C] | Bereich [C]

:----------|:---------------------------|:-------------|:----------------------|:--------------:

Merkur | 9126,49 | 0,088 | 345,83 | -180 bis 430

Venus | 2613,78 | 0,76 | 51,17 | 465

Erde | 1367,56 | 0,306 | 86,54 | -89 bis 58

Mars | 589,04 | 0,25 | 23,95 | -82 bis 0

Jupiter | 50,52 | 0,503 | -128,09 | -150

Saturn | 15,04 | 0,342 | -158,22 | -170

Uranus | 3,71 | 0,3 | -190,86 | -200

Neptun | 1,51 | 0,29 | -207,18 | -210

Es ist interessant zu bemerken, dass insbesondere bei Planeten, die der Sonne näher sind, Abweichungen auftreten, die durch ihre jeweiligen Atmosphären beeinflusst werden.

In diesem Modell werden Oberflächenvariationen und Änderungen der atmosphärischen Höhe nicht berücksichtigt. Daher wird der Planet als punktförmiges Objekt mit null Dimensionen (0D) modelliert.

ID:(4669, 0)

Beschreibung

>Top

Neben der Nutation unterliegt die Achse der Erde einer rotationsartigen Bewegung, die als Präzession bezeichnet wird.

None

Die Konsequenz der Präzession ist, dass sich der Zeitpunkt von Sommer und Winter im Laufe der Zeit ändert. Aufgrund einer Präzessionsperiode von 26.000 Jahren kehren sich alle 13.000 Jahre die Jahreszeiten um.

ID:(3087, 0)

Gleichung

>Top, >Modell

Si la intensidad visible del sol es I_s y el albedo de la superficie a_v, la intensidad reflejada será con

ID:(4668, 0)

Beschreibung

>Top

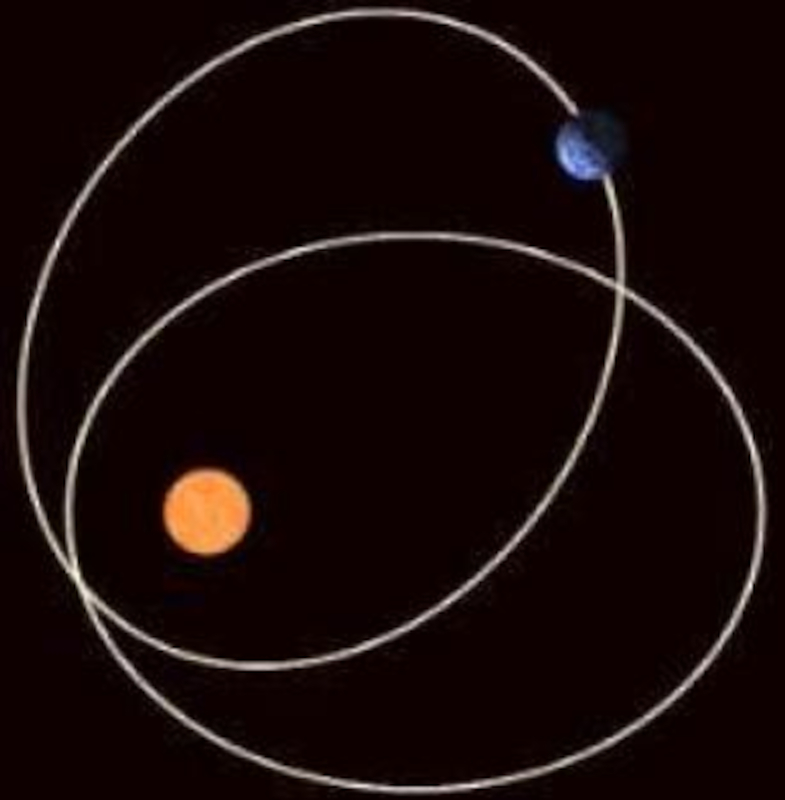
Die Intensität der Sonne schwankt je nach Genauigkeit der Umlaufbahn:

None

ID:(3089, 0)

Beschreibung

>Top

Die Neigung der Erdachse variiert zwischen 22,1 und 24,5 Grad. Dieser Prozess wird als Nutation bezeichnet.

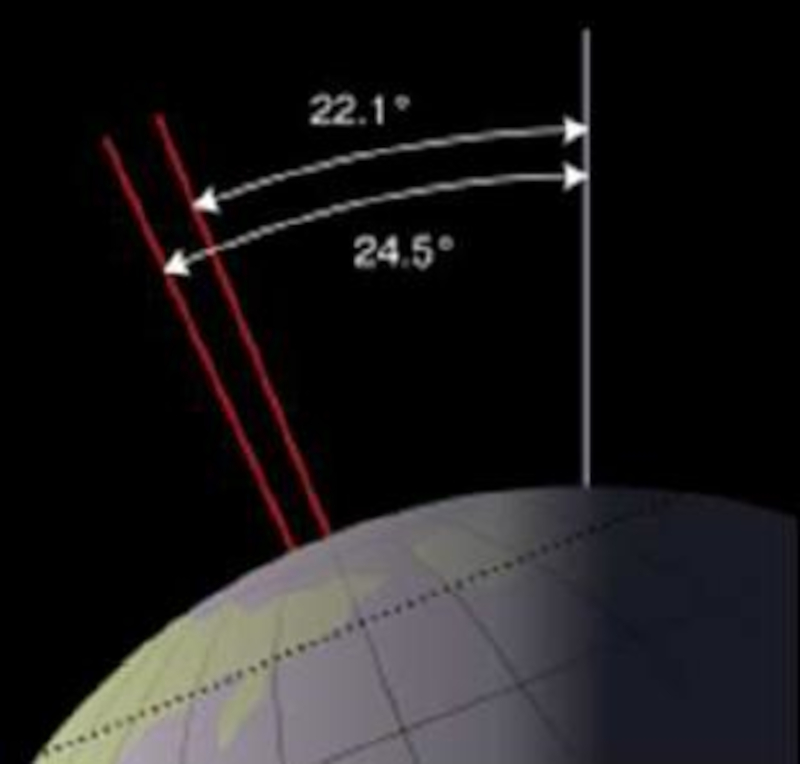
Die Nutation wird durch Effekte wie den Einfluss des Mondes auf die Erde und die nicht perfekt kugelförmige Form unseres Planeten verursacht. Jeder Effekt hat seine eigene typische Periode, wobei die längste etwa 41.000 Jahre beträgt. Es wird angenommen, dass der letzte maximale Wert vor etwa 10.700 Jahren (8700 v. Chr.) auftrat und mit dem Ende der letzten Eiszeit zusammenfiel.

ID:(3086, 0)

Beschreibung

>Top

Fluktuationen in der Ausrichtung der Erdachse und Variationen in der Umlaufbahn haben zu einer Abnahme der Sonnenstrahlung auf der Erde geführt, was zu Kälteperioden und der Entstehung von Eiszeitaltern geführt hat.

None

Das letzte Eiszeitalter endete vor etwa 10.000 Jahren.

ID:(3090, 0)