Usuario:
Transporte
Storyboard 
La convección transporta masas de aire y evaporación de agua generado en la superficie, lleva energía de la superficie a la atmósfera.
Las precipitaciones lleva energía de la atmósfera a la superficie.
Ambos procesos afectan el balance energético y con ello el clima.
ID:(1215, 0)
Distribución de calor transportado por calor latente
Descripción
Si observamos la distribución del calor transportado por calor latente en la superficie del planeta, se puede notar que depende de la humedad relativa. Por lo tanto, alcanza valores cercanos a $150 W/m^2$ sobre los océanos en zonas ecuatoriales, disminuyendo a $30 W/m^2$ en zonas continentales y llegando a cero en áreas desérticas:
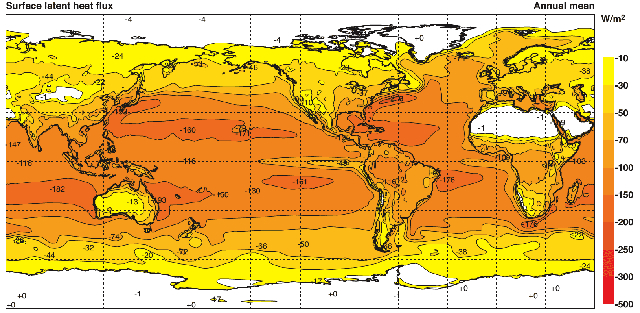
Promedio anual de calor transportado por calor latente calculado de ECMWF 40-años reanalizados (Kallberg et al 2005). Cuidado: este diagrama usa la convención de que un flujo ascendente es negativo a diferencia que el presente texto que la define como positiva.
Estos datos provienen del reanálisis de 40 años realizado por Kallberg P., Berrisford P., Hoskins B., Simmons A., Uppala S., Lamy-Thepaut S., Hine R., 2005: ERA-40 Atlas. Reading, Reino Unido, Proyecto de Reanálisis de ECMWF (Kallberg et al 2005).
ID:(9264, 0)
Mecanismo de calor transportado por convección
Imagen
Cuando el viento circula, desplaza masas de aire de temperatura más baja hacia zonas de mayor temperatura, lo que provoca una conducción de calor en el aire. A medida que el aire desplaza una masa de aire y trae una nueva con temperatura más baja, el proceso de transporte continúa sin detenerse, como se muestra en la imagen:
El viento desplaza aire previamente calentado y acarreando nuevo aire a menor temperatura
En este caso, podemos suponer que la temperatura del aire corresponde a la temperatura en la parte inferior de la atmósfera, $T_b.
ID:(3076, 0)
Mecanismo de transporte de calor latente
Descripción
Uno de los mecanismos clave en el proceso de flujo de energía en el sistema climático es la evaporación. En este proceso, el agua se evapora en un lugar, extrayendo energía de la superficie, y luego se transporta por convección hasta la atmósfera, donde libera nuevamente la energía mediante la condensación.
Ciclo del agua que indica los distintos flujos y los principales volúmenes de agua anuales.
La energía que fluye anualmente a través del transporte de calor latente es igual al flujo de $I_E\sim 80,W/m^2$ multiplicado por la superficie del planeta, con un radio $R\sim 6.37\times 10^{+6}m$ y el número de segundos en un año $t_e=3.15\times 10^{+7}s$.
$Q_e=4\pi R^2 I_E t_e=1.27\times 10^{24},J$
Si el calor latente es igual a $L_v=2256,kJ/kg$ y la densidad del agua es $\rho_w=1000,kg/m^3$, se obtiene el volumen de agua evaporada por año:
$V_w=\displaystyle\frac{Q_e}{\rho_wL_v}=5\times 10^{14}m^3$
De este volumen de agua, el 87% se evapora sobre los océanos, mientras que el resto proviene de zonas húmedas continentales. El agua regresa a la superficie a través de la lluvia o la nieve. Del total, el 77% corresponde a la lluvia sobre los océanos, lo cual es ligeramente superior a la proporción de superficie ocupada por los océanos.
ID:(9266, 0)
Diferencia de humedad relativa
Imagen
La humedad relativa promedio en la superficie de la tierra es del orden de
Como las nubes se forman por la condensación la atmósfera en esta zona debe de estar saturada. Si se asume que la atmósfera sin nubes no presenta mayor humedad entonces la humedad relativa debe ser del orden de la fracción de cobertura.
Con las humedades relativas es posible estimar las presiones de vapor de agua que existen sobre la superficie, borde inferior y superior de las nubes. Si se asumen las temperaturas de
| $ p_s = p_{ref} e^{- l_m / R T }$ |
y con la definición de humedad relativa
| $ RH =\displaystyle\frac{ p_v }{ p_s }$ |
concluir que la presiones de vapor de agua saturado
Altura | Temperatura [C] | $p_s$ [Pa] | HR [%] | $p_v$ [Pa]
:--------|:----------------:|:----------:|:----------:|:-----------:
Superficie | 14 | 1519 | 85 | 1291
Borde inferior | -1 | 588 | 42 | 247
Borde superior | -30 | 69 | 42 | 29
con lo que se puede asumir un valor promedio para la presión de vapor de agua en la atmósfera es 138 Pa y la diferencia tierra atmósfera 1154 Pa.
ID:(9268, 0)
Intensidad VIS que llega a la superficie del planeta
Ecuación
De la intensidad media de la tierra ($I_p$)6502, solo una fracción llega a la superficie de la Tierra. El factor que lo determina es la cobertura de atmósfera para radiación VIS ($\gamma_v$)6506, por lo que la intensidad VIS que llega a la superficie de la tierra ($I_{sev}$)6511 se expresa como:
| $ I_t =(1- \gamma ) I_s $ |
Con una intensidad solar de
$I_s \sim 342 W/m^2$
y una cobertura atmosférica de
$\gamma_v \sim 0.459$
la radiación que alcanza la superficie de la Tierra es:
$I_{sev} \sim 185 W/m^2$
Esto corresponde al 54.1% de la radiación solar. Esta radiación, que tiene en cuenta la pérdida de intensidad debido a la cobertura atmosférica, es lo que se conoce como insolación solar.
ID:(4673, 0)
Calor transportado por calor latente
Ecuación
El transporte de calor a través del calor latente, o flujo de calor latente (LHF) en inglés, ocurre además de la radiación infrarroja. Este fenómeno está aproximadamente relacionado con la diferencia de presiones de vapor de agua entre la superficie terrestre ($p_{v,e}$) y la atmósfera ($p_{v,a}$) de la siguiente manera:
 $I_E=c_aL_vC_Eu_z\displaystyle\frac{(p_{v,e}-p_{v,a})}{p_a}$ |
Si tomamos como referencia un flujo típico de calor transportado por calor latente de alrededor de $I_E\sim 80 W/m^2$, considerando una concentración molar del aire de $c_a\sim 42.4 mol/m^3$, el calor latente de evaporación $L_v\sim 40.6 kJ/mol$, una velocidad del viento del orden de $u_z\sim 8 m/s$, una diferencia de presión de vapor de agua del orden de $p_{ve}-p_{vb}\sim 1154 Pa$ y una presión atmosférica de $p\sim 10^5Pa$, se obtiene un coeficiente de transferencia de calor del orden de $C_E\sim 5.0\times 10^{-4}$.
ID:(9265, 0)
Calor transportado por convección
Ecuación
Además de la radiación infrarroja, existe un transporte de calor a través de la convección o el flujo de calor sensible (SHF). Ambos fenómenos son, en primera aproximación, proporcionales a la diferencia de temperatura entre la Tierra $T_e$ y la parte inferior de la atmósfera $T_b$:
| $ I_H = \rho_a c_p C_H u_z ( T_e - T_b )$ |
Si el flujo de calor típico transportado por convección es del orden de $I_H\sim 17 W/m^2$, y considerando que la densidad es del orden de $\rho_a\sim 1.225 kg/m^3$, la capacidad calorífica específica es $c_p\sim 1006.43 J/kg K$, y la velocidad del viento es del orden de $u_z\sim 8 m/s$, entonces, con una diferencia de temperatura de $T_e-T_b\sim 15.2 K$, el coeficiente de transferencia de calor es del orden de $C_H\sim 1.13\times 10^{-4}$.
ID:(4678, 0)
Simplificación transportado por calor latente
Ecuación
Dado que la concentración molar $c_a$ es proporcional a la presión $p_a$ según:
| $ p = c_m R T $ |
podemos reescribir
| $I_E=c_aL_vC_Eu_z\displaystyle\frac{(p_{v,e}-p_{v,a})}{p_a}$ |
como
| $ I_E = L_v C_E u_z \displaystyle\frac{( p_{v,e} - p_{v,a} )}{ R T_e }$ |
ID:(9275, 0)
Coeficiente constante de evaporación
Ecuación
El flujo de radiación debido a los elementos de transporte se expresa de la siguiente manera:
| $ I_d =( \kappa_l + \kappa_c ( T_e - T_b )) u $ |
donde se puede demostrar que el coeficiente constante de evaporación tiene la forma:
| $ \kappa_l = L_v C_E \displaystyle\frac{ p_{s,e} }{ R T_e }( RH_e - \gamma_v )$ |
Dado que el flujo de evaporación se puede expresar como:
| $I_E=c_aL_vC_Eu_z\displaystyle\frac{(p_{v,e}-p_{v,a})}{p_a}$ |
y queremos modelar el flujo como:
| $ I_d =( \kappa_l + \kappa_c ( T_e - T_b )) u $ |
podemos determinar el factor constante como:
| $ \kappa_l = L_v C_E \displaystyle\frac{ p_{s,e} }{ R T_e }( RH_e - \gamma_v )$ |
Si asumimos una concentración molar del aire de $c_a\sim 42.4$, un calor latente molar de $L_v\sim 40.6,kJ/mol$, una velocidad del viento de $u_z\sim 8,m/s$, una constante de transporte de calor latente de $C_E\sim 5.0\times 10^{-4}$, una presión de vapor de agua saturado de $p_{s,e}\sim 1519,Pa$, una humedad relativa de $RH_e\sim 85%$, una presión atmosférica de $p_a\sim 10^5,Pa$ y una cobertura visual de $\gamma_v\sim 42%$, la constante tiene un orden de magnitud de $\kappa_c\sim 5.66,J/m^3s$.
ID:(9271, 0)
Coeficiente de temperatura en el transporte
Ecuación
Dado que el flujo de transporte está dado por
| $ I_H = \rho_a c_p C_H u_z ( T_e - T_b )$ |
y el flujo de evaporación es
y se busca modelar el flujo como
| $ I_d =( \kappa_l + \kappa_c ( T_e - T_b )) u $ |
podemos determinar el factor de la temperatura como
| $ \kappa_c = \rho_a c_p C_H + C_E p_{s,e} \displaystyle\frac{ \gamma_v L_v ^2}{ R ^2 T_e ^3}$ |
Suponiendo que la densidad del aire es $\rho_a\sim 1.225,kg/m^3$, la concentración molar del aire es $c_a\sim 42.4$, el calor latente molar es $L_v\sim 40.6,kJ/mol$, la velocidad del viento es $u_z\sim 8,m/s$, la constante de transporte de calor es $C_H\sim 1.13\times 10^{-4}$ y la constante de transporte de calor latente es $C_E\sim 5.0\times 10^{-4}$, la presión de vapor de agua saturado es $p_{s,e}\sim 1519,Pa$, la humedad relativa es $RH_e\sim 85%$, la presión atmosférica es $p_a\sim 10^5,Pa$ y la cobertura visible es $\gamma_v\sim 42%$, el incremento de flujo por grado de diferencia de temperatura es del orden de $\kappa_c\sim 0.47,J/m^3s,K$.
ID:(9272, 0)
Flujo conducción y evaporación
Ecuación
La energía transmitido por conducción y evaporación ($I_d$)6522 depende de la diferencia entre la temperatura de la parte inferior de la atmósfera ($T_b$)6519 y la temperatura de la superficie de la tierra ($T_e$)6516, así como de la velocidad del viento ($u$)8094 y las constantes el coeficiente de calor latente ($\kappa_l$)8093 y el coeficiente de convección ($\kappa_c$)6521, de la siguiente manera:
| $ I_d =( \kappa_l + \kappa_c ( T_e - T_b )) u $ |
ID:(9270, 0)