Utilizador:
Cobertura visível (nuvens)
Descrição 
Em média, as nuvens cobrem mais de 40% da superfície da Terra:
Por serem visíveis, as nuvens refletem a luz, resultando em radiação visível e estão associadas ao albedo atmosférico.
ID:(3071, 0)
Estimativa da variação do albedo da atmosfera
Equação
Para estimar o albedo futuro da atmosfera $a_a$, adiciona-se ao albedo atual a variação $\delta a_a$:
 $ a_{at} = a_a + \delta a_a $ |
ID:(7483, 0)
Variações Visíveis de Cobertura
Equação
Da mesma forma, também devem ser consideradas as variações nos fatores de cobertura $\gamma_v$:
| $\gamma_{vt}=\gamma_v + \delta \gamma_v$ |
A mudança pode ser devida a variações no vapor de água e, consequentemente, na cobertura de nuvens. Portanto, a quantidade e distribuição de nuvens na atmosfera podem variar, o que afeta a quantidade de radiação solar que chega à superfície da Terra. Um maior fator de cobertura visível indica uma maior presença de nuvens, o que pode reduzir a quantidade de radiação solar direta e afetar o balanço energético da Terra.
A cobertura de nuvens visíveis desempenha um papel importante no sistema climático ao influenciar a distribuição de calor e a formação de precipitação. Ao considerar essas variações nos fatores de cobertura, podemos obter uma visão mais abrangente de como a radiação solar interage com a atmosfera e a superfície da Terra, e como isso afeta o clima e os padrões climáticos.
ID:(89, 0)
Estimativa de cobertura visível
Equação
A cobertura visível é em grande parte determinada pela relação entre a superfície coberta por nuvens $S_c$ e a superfície total do planeta $S_t$:
| $ \gamma_v =\displaystyle\frac{ S_c }{ S_t }$ |
o que corresponde a cerca de 42% na Terra.
ID:(7601, 0)
Estimativa de variação de cobertura visível
Equação
Para estimar a variação da cobertura visível, pode-se assumir, em uma primeira aproximação, uma relação linear com a variação do número de mols de água na atmosfera devido ao aumento da temperatura:
| $ \delta\gamma_v = c_v \displaystyle\frac{ \delta c }{ c }$ |
ID:(7589, 0)
Absorção de radiação pela atmosfera
Video
Em nível molecular, as moléculas podem oscilar com frequências que dependem de sua geometria. Isso significa que, quando a radiação atravessa um gás composto por moléculas e sua frequência coincide com uma das frequências naturais de oscilação dessas moléculas, a radiação será absorvida pelo gás. Como resultado, uma parte da radiação que atravessa a atmosfera é retida, dando origem à cobertura observada nos modelos climáticos.
Aqui está um vídeo histórico (de 1960) que mostra como as moléculas vibram de acordo com sua geometria:
Descrição do vídeo no YouTube:
O Estudo de Materiais Educacionais em Química, conhecido como Estudo CHEM, foi desenvolvido no início da década de 1960 na UC Berkeley\'s College of Chemistry, Lawrence Hall of Science e Harvey Mudd College, e continuou no Lawrence Hall of Science até a década de 1980. O livro didático foi escrito por Glenn T. Seaborg no início da década de 1960.
ID:(7330, 0)
Como funcionam os gases de efeito estufa
Imagem
A atmosfera contém vários gases que podem absorver a radiação que passa por ela. No espectro visível, é principalmente o vapor de água, e no espectro infravermelho, são o dióxido de carbono ($CO_2$), o metano ($CH_4$) e o óxido nitroso ($N_2O$).
Isso pode ser visualizado graficamente através dos espectros. A linha amarela representa o espectro como é emitido: na parte superior, pelo sol (visível) e pela terra (infravermelho). A linha vermelha mostra o que resta do espectro após ter passado pela atmosfera, destacando claramente as frequências que não conseguem atravessar devido à absorção:
ID:(10844, 0)
Variações de cobertura de infravermelho (NIR)
Equação
Da mesma forma, também devem ser consideradas as variações nos fatores de cobertura infravermelha $\gamma_i$:
| $\gamma_{it}=\gamma_i + \delta \gamma_i$ |
A variação na cobertura infravermelha ocorre principalmente devido a mudanças nos gases de efeito estufa e no vapor de água, resultantes de flutuações ambientais. Essas mudanças podem ser resultado de variações climáticas naturais e/ou ações humanas.
Os gases de efeito estufa, como dióxido de carbono (CO2), metano (CH4) e óxido nitroso (N2O), têm a capacidade de absorver e emitir radiação infravermelha, contribuindo para o efeito estufa e o aquecimento global. Atividades humanas, como a queima de combustíveis fósseis e o desmatamento, podem aumentar a concentração desses gases na atmosfera e, portanto, afetar a cobertura infravermelha.
Estudar e compreender essas variações nos fatores de cobertura infravermelha é importante para avaliar seu impacto no clima e no equilíbrio energético da Terra. Isso nos permite tomar medidas adequadas para mitigar os efeitos das mudanças climáticas e promover práticas sustentáveis.
ID:(7533, 0)
Variação do Fator de Cobertura Infravermelha
Equação
A variação do fator de cobertura infravermelho (IR) está associada à variação dos gases de efeito estufa. Eles são medidos em partes por milhão $ppm$ e partes por bilhão $ppb$, calculados a partir da densidade do gás $\rho$ no ar, conforme:
$ppmv =\displaystyle\frac{Gás}{10^6 Ar}=\displaystyle\frac{V_n}{M_g}\displaystyle\frac{10^{-6}g,Gás}{l,Ar}$
e
$ppbv =\displaystyle\frac{Gás}{10^9 Ar}=\displaystyle\frac{V_n}{M_g}\displaystyle\frac{10^{-9}g,Gás}{l,Ar}$
Onde $M_g$ é a massa molar do gás e $V_n$ é o volume nas condições normais (temperatura $0^{\circ}C$, pressão $10^5 Pa$, que corresponde a $22.71108 l$).
Como exemplo, se considerarmos o nível atual de $CO_2$ (massa molar de $44.0 g/mol$), veremos que a concentração de $379 ppmv$ (em 2005) corresponde a $0.736 g/l$ de $CO_2$. Para determinar a quantidade de $CO_2$ presente na atmosfera, precisamos saber quantos litros de ar existem. Como a camada teoricamente é infinita (cada vez mais diluída, mas ainda presente), temos um problema ao definir a altura da camada de ar. No entanto, se considerarmos que, pela lei barométrica, a pressão diminui conforme:
$p(z) = p_0 e^{M_agz/RT}$
Temos, de forma análoga, para a densidade:
$\rho(z) = \rho_0 e^{M_ag z/RT}$
Se integramos essa equação em relação a z, observamos que a quantidade é tal que todo o ar se concentraria com densidade da superfície em uma camada de altura
$z_0 =\displaystyle\frac{RT}{M_ag}= 8001.78m$
a uma temperatura de zero grau Celsius. Em outras palavras, o volume total de $CO_2$ na atmosfera pode ser calculado multiplicando a densidade estimada pelo volume de uma camada de $8001.78 m$ de altura que se estende por todo o planeta. Supondo um raio da Terra de $6370 km$ e uma densidade de $0.736e-3 g/L$, obtemos que a camada de altura $8001.78 m$ tem uma massa de $CO_2$ de $3000 Gt CO_2$.
Como a massa molar do carbono é de $12 g/mol$ e a do $CO_2$ é de $44.1 g/mol$, a massa de carbono na atmosfera é de $3000\cdot 14/44.1$, o que equivale a $817 Gt C$. A relação entre concentração e forçamento radiativo pode ser obtida na tabela na próxima página. As informações dos cenários indicam a quantidade de gases adicionados à atmosfera anualmente. Em geral, o forçamento radiativo FR está relacionado à variação da temperatura na atmosfera, conforme
$\Delta T = \delta T_b - \delta T_t$
is
| $ \Delta T = \lambda FR $ |
onde $\lambda$ é a sensibilidade climática que corresponde a $0.8 Km^2/W$. No caso do $CO_2$, podemos considerar o aumento de $13 ppm$ e o forçamento radiativo de $1.66 W/m^2$.
ID:(7323, 0)
Estimativa de variação da cobertura infravermelha total (NIR)
Equação
Para obter a cobertura total no infravermelho (NIR), representada como $\delta\gamma_i$, é necessário somar as contribuições de cada gás:
| $ \delta\gamma_{i,k} =\displaystyle\frac{ \Delta F_k }{(1- a_a ) I_s }\displaystyle\frac{ \delta c_k }{ c_k }$ |
onde $\alpha_{ij}$ representa a contribuição do gás $j$ para a cobertura no infravermelho do gás $i$. A soma é realizada para todos os gases relevantes.
Portanto, a variação na cobertura total no infravermelho pode ser calculada usando:
| $ \delta\gamma_i =\displaystyle\sum_k \delta\gamma_{i,k} $ |
Essa equação fornece a diferença relativa entre os valores finais e iniciais da cobertura no infravermelho.
É importante ressaltar que essas equações são uma representação simplificada dos processos envolvidos no cálculo da cobertura total no infravermelho e sua variação. Os cálculos reais podem levar em consideração fatores adicionais e complexidades específicas do sistema ou cenário sendo analisado.
ID:(10831, 0)
Estimativa da variação da cobertura infravermelha de um gás
Equação
A força radiativa $\Delta F_k$ para o gás de efeito estufa $k$ contribui com base na radiação que incide no planeta, que é igual à intensidade de insolamento solar $I_s$ multiplicada por $(1-a_a)$, onde $a_a$ é o albedo atmosférico.
Ao aumentar a concentração $c_k$ em uma quantidade $\delta c_k$, o aumento do fluxo que incide a partir da atmosfera é dado por:
| $ \delta\gamma_{i,k} =\displaystyle\frac{ \Delta F_k }{(1- a_a ) I_s }\displaystyle\frac{ \delta c_k }{ c_k }$ |
ID:(7590, 0)
Forçante radiativa dos gases principais
Descrição
No diagrama, é apresentado o forçamento radiativo dos principais gases na atmosfera:
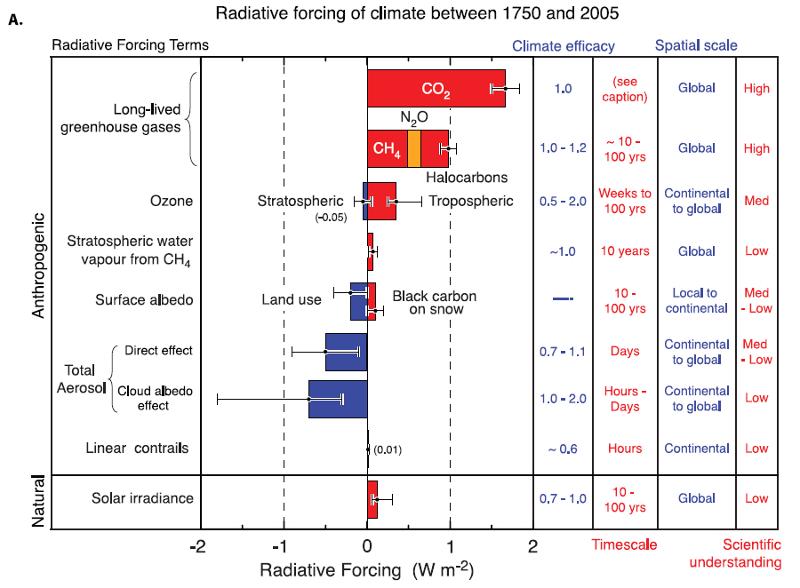
Este diagrama ilustra a contribuição relativa dos diferentes gases para o forçamento radiativo da atmosfera. Cada gás tem seu próprio impacto no aquecimento ou resfriamento do sistema climático.
Alguns gases, como o dióxido de carbono (CO2) e o metano (CH4), são gases de efeito estufa que retêm o calor na atmosfera e contribuem para o aquecimento global. Outros gases, como o óxido nitroso (N2O), também têm um efeito de aquecimento.
Por outro lado, alguns gases, como o dióxido de enxofre (SO2) e os aerossóis de sulfato, têm um efeito de resfriamento ao refletir a radiação solar e reduzir a quantidade de energia que chega à superfície da Terra.
Compreender a importância relativa desses gases no forçamento radiativo é crucial para avaliar seu impacto nas mudanças climáticas e para desenvolver estratégias eficazes de mitigação.
ID:(7325, 0)
Forçante radiativa de outros gases e aerossóis
Descrição
No gráfico são mostradas as forçantes radiativas de outros gases e aerossóis. Alguns deles contribuem para o resfriamento do planeta:
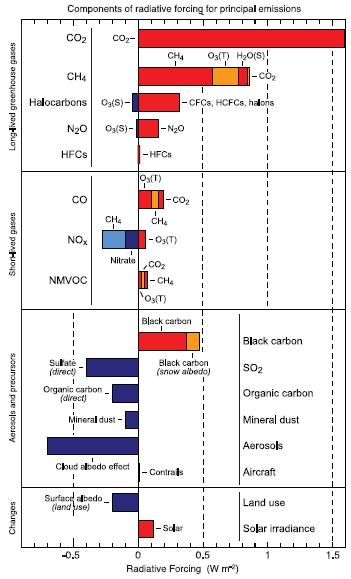
Essas forçantes radiativas representam a influência de diferentes gases e aerossóis no balanço energético da Terra. Alguns gases, como o dióxido de enxofre (SO2) e os aerossóis de sulfato, possuem efeitos de resfriamento ao refletir a radiação solar e reduzir a quantidade de radiação que atinge a superfície terrestre.
É importante compreender a contribuição desses gases e aerossóis no balanço radiativo global, pois eles têm implicações significativas para o clima e podem influenciar os padrões climáticos e o aquecimento global. Estudar e avaliar seu impacto nos permite tomar medidas adequadas para lidar com as mudanças climáticas e buscar soluções sustentáveis.
ID:(7326, 0)
Forçamento radiativo ao longo do tempo
Descrição
O gráfico apresenta as projeções das forçantes radiativas esperadas nos horizontes de 20 e 100 anos:
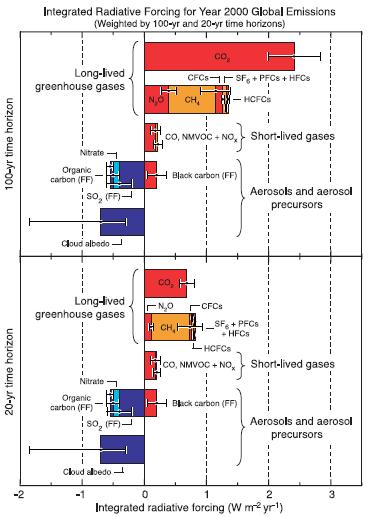
Essas projeções representam cenários potenciais de forçantes radiativas no futuro próximo e distante. É importante ressaltar que essas projeções são baseadas em modelos e suposições científicas atuais e estão sujeitas a incertezas.
A análise das forçantes radiativas a longo prazo é fundamental para compreender os possíveis impactos no clima e no aquecimento global. Esses resultados podem contribuir para informar políticas e ações que visem mitigar os efeitos das mudanças climáticas e promover a sustentabilidade ambiental.
ID:(7327, 0)
Mudanças na atmosfera
Descrição
Uma situação que ilustra o impacto da cobertura no clima ocorreu durante a proibição de voos comerciais por três dias após o ataque às Torres Gêmeas. A ausência de voos comerciais por 72 horas resultou em uma diminuição das trilhas de condensação (contrails), o que, por sua vez, levou a uma mudança na cobertura de nuvens e à redução das nuvens cirrus.
ID:(9247, 0)