Utilisateur:
Couverture visible (nuages)
Description 
En moyenne, les nuages couvrent plus de 40% de la surface de la Terre :
Étant visibles, les nuages reflètent la lumière, ce qui se traduit par un rayonnement visible et est associé à l\'albédo atmosphérique.
ID:(3071, 0)
Estimation de la variation de l\'albédo de l\'atmosphère
Équation
Pour estimer l\'albédo futur de l\'atmosphère $a_a$, on ajoute à l\'albédo actuel la variation $\delta a_a$:
 $ a_{at} = a_a + \delta a_a $ |
ID:(7483, 0)
Variations de couverture visibles
Équation
De la même manière, il convient également de tenir compte des variations des facteurs de couverture $\gamma_v$ :
| $\gamma_{vt}=\gamma_v + \delta \gamma_v$ |
Le changement peut être dû à des variations dans la vapeur d\'eau et, par conséquent, à la couverture nuageuse. Ainsi, la quantité et la répartition des nuages dans l\'atmosphère peuvent varier, ce qui affecte la quantité de rayonnement solaire atteignant la surface de la Terre. Un facteur de couverture visible plus élevé indique une présence accrue de nuages, ce qui peut réduire la quantité de rayonnement solaire direct et avoir un impact sur le bilan énergétique de la Terre.
La couverture nuageuse visible joue un rôle important dans le système climatique en influençant la distribution de la chaleur et la formation des précipitations. En tenant compte de ces variations des facteurs de couverture, nous pouvons obtenir une vision plus complète de la manière dont le rayonnement solaire interagit avec l\'atmosphère et la surface de la Terre, et de son impact sur le climat et les schémas climatiques.
ID:(89, 0)
Estimation de la couverture visible
Équation
La couverture visible est en grande partie déterminée par le rapport entre la surface couverte par les nuages $S_c$ et la surface totale de la planète $S_t$ :
| $ \gamma_v =\displaystyle\frac{ S_c }{ S_t }$ |
ce qui correspond à environ 42% sur Terre.
ID:(7601, 0)
Estimation de la variation de la couverture visible
Équation
Pour estimer la variation de la couverture visible, on peut supposer, dans une première approximation, une relation linéaire avec la variation du nombre de moles d\'eau dans l\'atmosphère due à l\'augmentation de la température:
| $ \delta\gamma_v = c_v \displaystyle\frac{ \delta c }{ c }$ |
ID:(7589, 0)
Absorption du rayonnement par l\'atmosphère
Video
Au niveau moléculaire, les molécules peuvent osciller avec des fréquences qui dépendent de leur géométrie. Cela signifie que si le rayonnement traverse un gaz de molécules et que sa fréquence est similaire à l\'une des fréquences propres d\'oscillation des molécules, il sera absorbé par le gaz. Ainsi, une partie du rayonnement qui traverse l\'atmosphère est retenue, ce qui donne lieu à l\'absorption observée dans les modèles climatiques.
Voici une vidéo historique (de 1960) montrant comment les molécules vibrent en fonction de leur géométrie :
Description de la vidéo sur YouTube :
L\'étude des matériaux éducatifs en chimie, plus connue sous le nom d\'étude CHEM, a été réalisée au début des années 1960 à la faculté de chimie de l\'UC Berkeley, au Lawrence Hall of Science et au Harvey Mudd College, et s\'est poursuivie au Lawrence Hall of Science jusqu\'aux années 1980. Le manuel a été rédigé par Glenn T. Seaborg au début des années 1960.
ID:(7330, 0)
Comment fonctionnent les gaz à effet de serre
Image
L'atmosphère contient divers gaz qui peuvent absorber la radiation qui la traverse. Dans le spectre visible, c'est principalement la vapeur d'eau, et dans le spectre infrarouge, ce sont le dioxyde de carbone ($CO_2$), le méthane ($CH_4$) et le protoxyde d'azote ($N_2O$).
Cela peut être visualisé graphiquement à travers les spectres. La ligne jaune représente le spectre tel qu'il est émis : en haut, par le soleil (visible) et par la terre (infrarouge). La ligne rouge montre ce qui reste du spectre après son passage à travers l'atmosphère, mettant clairement en évidence les fréquences qui ne passent pas en raison de l'absorption :
ID:(10844, 0)
Variations de la couverture infrarouge (NIR)
Équation
De la même manière, il convient également de tenir compte des variations des facteurs de couverture infrarouge $\gamma_i$ :
| $\gamma_{it}=\gamma_i + \delta \gamma_i$ |
La variation de la couverture infrarouge est principalement due aux changements dans les gaz à effet de serre et à la vapeur d\'eau, qui résultent des fluctuations environnementales. Ces changements peuvent être le résultat de variations climatiques naturelles et/ou d\'activités humaines.
Les gaz à effet de serre tels que le dioxyde de carbone (CO2), le méthane (CH4) et l\'oxyde nitreux (N2O) ont la capacité d\'absorber et d\'émettre un rayonnement infrarouge, contribuant à l\'effet de serre et au réchauffement climatique. Les activités humaines telles que la combustion de combustibles fossiles et la déforestation peuvent augmenter la concentration de ces gaz dans l\'atmosphère et donc influencer la couverture infrarouge.
Étudier et comprendre ces variations des facteurs de couverture infrarouge est important pour évaluer leur impact sur le climat et l\'équilibre énergétique de la Terre. Cela nous permet de prendre des mesures appropriées pour atténuer les effets du changement climatique et promouvoir des pratiques durables.
ID:(7533, 0)
Variation du facteur de couverture infrarouge
Équation
La variation du facteur de couverture infrarouge (IR) est associée à la variation des gaz à effet de serre. Ils sont mesurés en parties par million $ppm$ et en parties par milliard $ppb$, calculés à partir de la densité du gaz $\rho$ dans l\'air, selon les équations suivantes :
$ppmv =\displaystyle\frac{Gaz}{10^6 Air}=\displaystyle\frac{V_n}{M_g}\displaystyle\frac{10^{-6}g,Gaz}{l,Air}$
et
$ppbv =\displaystyle\frac{Gaz}{10^9 Air}=\displaystyle\frac{V_n}{M_g}\displaystyle\frac{10^{-9}g,Gaz}{l,Air}$
Où $M_g$ est la masse molaire du gaz et $V_n$ est le volume dans des conditions normales (température 0°C, pression $10^5 Pa$, ce qui correspond à $22.71108 L$).
À titre d\'exemple, si nous considérons le niveau actuel de $CO_2$ (masse molaire de $44.0 g/mol$), nous constatons qu\'une concentration de $379 ppmv$ (en 2005) correspond à $0.736 g/l$ de $CO_2$. Pour connaître la quantité de $CO_2$ présente dans l\'atmosphère, nous devons savoir combien de litres d\'air existent. Étant donné que la couche est théoriquement infinie (de plus en plus diluée mais toujours présente), nous avons un problème pour définir la hauteur de la couche d\'air. Cependant, si nous considérons que, selon la loi barométrique, la pression diminue selon :
$p(z) = p_0 e^{M_agz/RT}$
Nous obtenons de manière analogue la densité :
$\rho(z) = \rho_0 e^{M_ag z/RT}$
Si nous intégrons cette équation par rapport à z, nous observons que la quantité est telle que tout l\'air se concentrerait avec une densité de surface dans une couche d\'une hauteur de
$z_0 =\displaystyle\frac{RT}{M_ag}= 8001.78m$
à une température de zéro degré Celsius. En d\'autres termes, le volume total de $CO_2$ dans l\'atmosphère peut être calculé en multipliant la densité estimée par le volume d\'une couche de $8001.78 m$ de hauteur qui s\'étend sur toute la planète. En supposant un rayon de la Terre de $6370 km$ et une densité de $0.736e-3 g/L$, on obtient que la couche de hauteur $8001.78 m$ a une masse de $CO_2$ de $3000 Gt CO_2$.
Comme la masse molaire du carbone est de $12 g/mol$ et celle du $CO_2$ est de $44.1 g/mol$, la masse de carbone dans l\'atmosphère est de $3000\cdot 14/44.1$, ce qui donne $817 Gt C$. La relation entre la concentration et le forçage radiatif peut être obtenue à partir du tableau à la page suivante. Les informations disponibles sur les scénarios indiquent la quantité de gaz ajoutée à l\'atmosphère chaque année. En général, le forçage radiatif FR est lié à la variation de la température dans l\'atmosphère selon l\'équation :
$\Delta T = \delta T_b - \delta T_t$
is
| $ \Delta T = \lambda FR $ |
où $\lambda$ est la sensibilité climatique correspondant à $0.8 Km^2/W$. Dans le cas du $CO_2$, nous pouvons considérer une augmentation de $13 ppm$ et un forçage radiatif de $1.66 W/m^2$.
ID:(7323, 0)
Estimation de la variation de la couverture infrarouge totale (NIR)
Équation
Pour obtenir la couverture totale dans l\'infrarouge (NIR), représentée par $\delta\gamma_i$, il est nécessaire de faire la somme des contributions de chaque gaz:
| $ \delta\gamma_{i,k} =\displaystyle\frac{ \Delta F_k }{(1- a_a ) I_s }\displaystyle\frac{ \delta c_k }{ c_k }$ |
où $\alpha_{ij}$ représente la contribution du gaz $j$ à la couverture infrarouge du gaz $i$. La somme est effectuée pour tous les gaz pertinents.
Ainsi, la variation de la couverture totale dans l\'infrarouge peut être calculée à l\'aide:
| $ \delta\gamma_i =\displaystyle\sum_k \delta\gamma_{i,k} $ |
Cette équation fournit la différence relative entre les valeurs finales et initiales de la couverture infrarouge.
Il est important de noter que ces équations sont une représentation simplifiée des processus impliqués dans le calcul de la couverture totale dans l\'infrarouge et de sa variation. Les calculs réels peuvent prendre en compte des facteurs supplémentaires et des complexités spécifiques au système ou au scénario étudié.
ID:(10831, 0)
Estimation de la variation de couverture infrarouge d\'un gaz
Équation
Le forçage radiatif $\Delta F_k$ pour le gaz à effet de serre $k$ contribue en fonction du rayonnement qui pénètre dans la planète, qui est égal à l\'intensité de l\'insolation solaire $I_s$ multipliée par $(1-a_a)$, où $a_a$ est l\'albédo atmosphérique.
En augmentant la concentration $c_k$ d\'une quantité $\delta c_k$, l\'augmentation du flux qui pénètre depuis l\'atmosphère est donnée par :
| $ \delta\gamma_{i,k} =\displaystyle\frac{ \Delta F_k }{(1- a_a ) I_s }\displaystyle\frac{ \delta c_k }{ c_k }$ |
ID:(7590, 0)
Forçage radiatif des gaz principaux
Description
Le diagramme montre le forçage radiatif des principaux gaz dans l\'atmosphère :
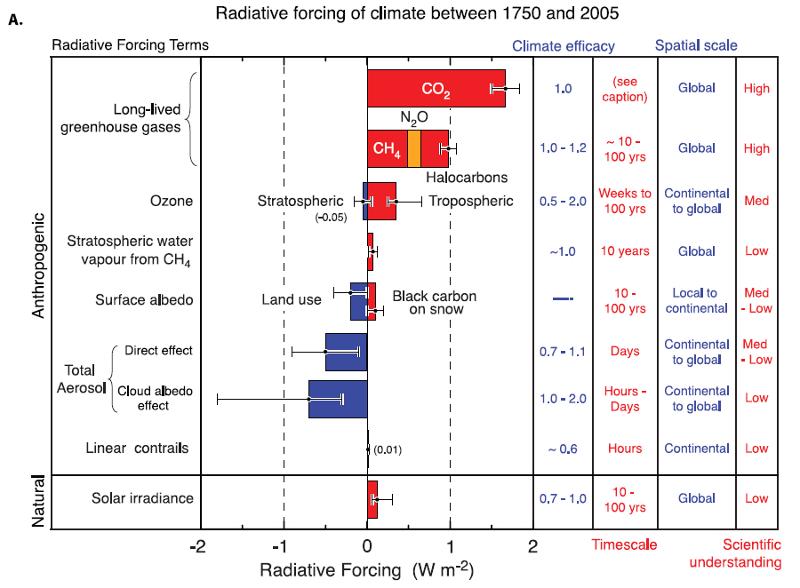
Ce diagramme illustre la contribution relative des différents gaz au forçage radiatif de l\'atmosphère. Chaque gaz a son propre impact sur le réchauffement ou le refroidissement du système climatique.
Certains gaz, tels que le dioxyde de carbone (CO2) et le méthane (CH4), sont des gaz à effet de serre qui retiennent la chaleur dans l\'atmosphère et contribuent au réchauffement climatique. D\'autres gaz, tels que le protoxyde d\'azote (N2O), ont également un effet de réchauffement.
En revanche, certains gaz, comme le dioxyde de soufre (SO2) et les aérosols de sulfate, ont un effet de refroidissement en réfléchissant le rayonnement solaire et en réduisant la quantité d\'énergie qui atteint la surface de la Terre.
Comprendre l\'importance relative de ces gaz dans le forçage radiatif est crucial pour évaluer leur impact sur le changement climatique et pour développer des stratégies d\'atténuation efficaces.
ID:(7325, 0)
Forçage radiatif des autres gaz et aérosols
Description
Le graphique présente les forçages radiatifs d\'autres gaz et aérosols. Certains d\'entre eux contribuent à refroidir la planète :
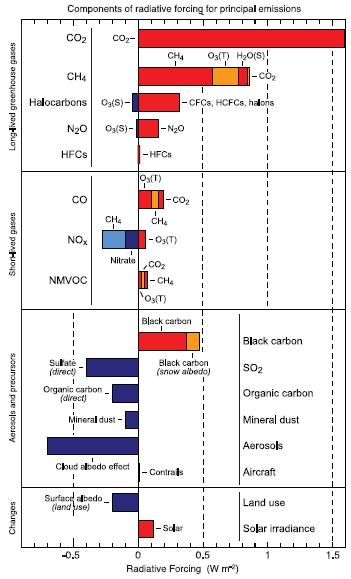
Ces forçages radiatifs représentent l\'influence de différents gaz et aérosols sur le bilan énergétique de la Terre. Certains gaz, tels que le dioxyde de soufre (SO2) et les aérosols de sulfate, ont des effets de refroidissement en réfléchissant le rayonnement solaire et en réduisant la quantité de rayonnement atteignant la surface terrestre.
Il est important de comprendre la contribution de ces gaz et aérosols à l\'équilibre radiatif global, car ils ont des implications significatives pour le climat et peuvent influencer les schémas climatiques et le réchauffement global. Étudier et évaluer leur impact nous permet de prendre les mesures appropriées pour faire face au changement climatique et rechercher des solutions durables.
ID:(7326, 0)
Forçage radiatif dans le temps
Description
Le graphique présente les projections des forçages radiatifs attendus sur les horizons de 20 et 100 ans :
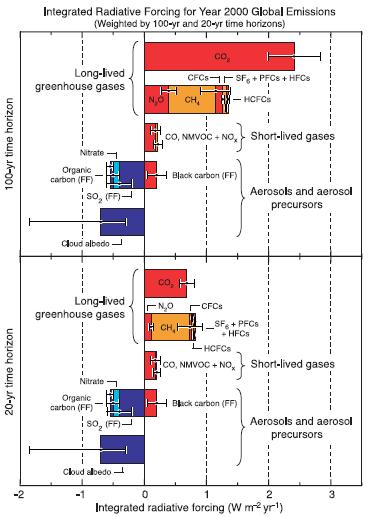
Ces projections représentent des scénarios potentiels de forçages radiatifs dans un avenir proche et lointain. Il est important de noter que ces projections sont basées sur des modèles scientifiques et des hypothèses actuelles et sont sujettes à des incertitudes.
L\'analyse des forçages radiatifs à long terme est essentielle pour comprendre les impacts potentiels sur le climat et le réchauffement global. Ces résultats peuvent contribuer à éclairer les politiques et les actions visant à atténuer les effets du changement climatique et à promouvoir la durabilité environnementale.
ID:(7327, 0)
Changements d'atmosphère
Description
Une situation illustrant l'impact de la couverture sur le climat s'est produite pendant l'interdiction des vols commerciaux pendant trois jours après l'attaque des tours jumelles. L'absence de vols commerciaux pendant 72 heures a entraîné une diminution des traînées de condensation (contrails), ce qui a conduit à un changement de la couverture nuageuse et à une réduction des nuages cirrus.
ID:(9247, 0)