Usuario:
Cambios en la atmósfera
Storyboard 
Los posibles cambios en la atmósfera son variados y van de cambios en el tipo de nubosidad, lo que afecta el albedo atmosférico, a variaciones de la cobertura. En el rango visible esto es ante todo la formación de mas nubes o la evaporación de estas. En el rango infrarrojo, que se asocia en especial a los gases invernadero, varia la cobertura infrarroja.
ID:(576, 0)
Cobertura visible (nubes)
Descripción
En promedio, las nubes cubren más del 40% de la superficie de la Tierra:
Cobertura de nubes
Dado que son visibles, las nubes reflejan la luz, lo que se traduce en radiación visible y está relacionado con el albedo atmosférico.
ID:(3071, 0)
Albedos atmosféricos según tipo de nube
Descripción
Las principales nubes y los rangos de altura y albedo se indican en la siguiente tabla:
Cumulus (Cu) 11.49% | Stratocumulus (Sc) 12.07% | Stratus (St) 1.76% | |
| Grosor optico | 0.0-3.6 | 3.6-23 | 23-379 |
ID:(7532, 0)
Estimación de variación del albedo de la atmósfera
Ecuación
Para estimar el albedo futuro de la atmósfera $a_a$, se suma al albedo actual la variación $\delta a_a$:
 $ a_{at} = a_a + \delta a_a $ |
ID:(7483, 0)
Coberturas según tipo de nube
Variable
Los distintos tipos de nubes cubren distintas fracciones de la superficie terrestre.
ID:(9980, 0)
Suma de superficies de nubes
Ecuación
Las superficies total de las nubes
| $S_a=\displaystyle\sum_iS_{a,i}$ |
ID:(7500, 0)
Fracción de cobertura de nubes por tipo
Ecuación
Para modelar el comportamiento climático se segmenta el globo en sectores de similar albedo que en el caso de la atmósfera se puede clasificar por tipo de nube. La fracción de cada tipo de nube se puede calcular de la superficie total de nubes sobre el planeta:
| $s_{a,i}=\displaystyle\frac{S_{a,i}}{S_a}$ |
ID:(10062, 0)
Calculo del albedo atmosférico
Ecuación
También aquí el albedo total es la suma ponderada de los albedos de las distintas zonas de la superficie
| $s_{a,i}=\displaystyle\frac{S_{a,i}}{S_a}$ |
según el tipo de nubosidad que exista. Por ello se tiene que
| $a_a =\displaystyle\sum_i s_{a,i}a_{a,i}$ |
ID:(7439, 0)
Fracción de la variación de la cobertura de nubes por tipo
Ecuación
Al igual que se clasifica sectores de nubes con similar albedo, se puede hacer lo análogo con las variaciones de dichas coberturas. En este caso se definen las relaciones:
| $\delta s_{a,i}=\displaystyle\frac{\delta S_{a,i}}{S_a}$ |
ID:(10063, 0)
Suma de variación de la cobertura de las nubes
Ecuación
La variación de la cobertura de las nubes debe ser nula ya que se expresan en función de la superficie total de nubes:
| $\sum_i\delta s_{a,i}=0$ |
ID:(7502, 0)
Calculo del cambio del albedo atmosférico
Ecuación
También aquí el albedo total es la suma ponderada de los albedos de las distintas zonas de la superficie
| $\delta s_{a,i}=\displaystyle\frac{\delta S_{a,i}}{S_a}$ |
según el tipo de nubosidad que exista. Por ello se tiene que
| $a_a =\displaystyle\sum_i s_{a,i}a_{a,i}$ |
y en forma análoga la variación del albedo es
| $\delta a_a =\displaystyle\sum_i\delta s_{a,i}a_{a,i}$ |
ID:(7322, 0)
Variaciones de la cobertura visible
Ecuación
De igual forma, también se deben considerar las variaciones en los factores de cobertura $\gamma_v$:
| $\gamma_{vt}=\gamma_v + \delta \gamma_v$ |
El cambio puede ser debido a variaciones en el vapor de agua y, por lo tanto, a la nubosidad. La cantidad y distribución de nubes en la atmósfera pueden variar, lo que afecta la cantidad de radiación solar que llega a la superficie terrestre. Un mayor factor de cobertura visible indica una mayor presencia de nubes, lo que puede reducir la cantidad de radiación solar directa y afectar el balance energético de la Tierra.
La nubosidad visible juega un papel importante en el sistema climático al influir en la distribución del calor y la formación de precipitaciones. Al considerar estas variaciones en los factores de cobertura, podemos obtener una visión más completa de cómo la radiación solar interactúa con la atmósfera y la superficie terrestre, y cómo afecta el clima y los patrones climáticos.
ID:(89, 0)
Estimación de la cobertura visible
Ecuación
La cobertura visible es en gran medida la relación entre la superficie cubierta por nubes $S_c$ y la superficie total del planeta $S_t$:
| $ \gamma_v =\displaystyle\frac{ S_c }{ S_t }$ |
lo que en la Tierra es del orden de 42%.
ID:(7601, 0)
Estimación de variación de cobertura visible
Ecuación
Para estimar la variación de la cobertura visible, se puede asumir, en una primera aproximación, una relación lineal con la variación de moles de agua en la atmósfera debido al aumento de temperatura:
| $ \delta\gamma_v = c_v \displaystyle\frac{ \delta c }{ c }$ |
ID:(7589, 0)
Absorción de radiación por la atmósfera
Video
Las moléculas pueden oscilar con frecuencias que dependen de su geometría. Esto significa que cuando la radiación atraviesa un gas compuesto por moléculas, si su frecuencia coincide con alguna de las frecuencias de oscilación propia de esas moléculas, la radiación será absorbida por el gas. Por lo tanto, una parte de la radiación que atraviesa la atmósfera será retenida, lo que da origen a la cobertura que observamos en los modelos climáticos.
A continuación, se muestra un video histórico (de 1960) que ilustra cómo las moléculas vibran en función de su geometría:
Vibration of Molecules CHEM Study
Descripción del video en YouTube:
El Estudio de Materiales Educativos Químicos, conocido como Estudio CHEM, se llevó a cabo a principios de la década de 1960 en la Universidad de California, la Facultad de Química de Berkeley, el Lawrence Hall of Science y el Harvey Mudd College. Continuó en el Lawrence Hall of Science hasta la década de 1980. El libro de texto fue escrito por Glenn T. Seaborg a principios de los años sesenta.
ID:(7330, 0)
Forma como trabajan gases invernadero
Imagen
La atmósfera contiene varios gases que pueden absorber la radiación que pasa a través de ella. En el rango visible, es principalmente el vapor de agua, y en el rango infrarrojo, son el dióxido de carbono ($CO_2$), el metano ($CH_4$) y el óxido nitroso ($N_2O$).
Esto se puede visualizar gráficamente mediante los espectros. La línea amarilla representa el espectro tal como se emite: en la parte superior, por el sol (visible) y por la tierra (infrarrojo). En rojo se muestra el espectro restante después de haber atravesado la atmósfera, destacándose claramente las frecuencias que no logran pasar debido a la absorción:
Espectro visible e infrarrojo (Wikipedia)
ID:(10844, 0)
Variaciones de la cobertura infrarrojo (NIR)
Ecuación
De igual forma, también deben considerarse las variaciones en los factores de cobertura infrarroja $\gamma_i$:
| $\gamma_{it}=\gamma_i + \delta \gamma_i$ |
La cobertura infrarroja varía principalmente debido a las fluctuaciones en los gases de efecto invernadero y en el vapor de agua, que son resultado de cambios ambientales. Estos cambios pueden ser causados por variaciones climáticas naturales y/o por acciones humanas.
Los gases de efecto invernadero, como el dióxido de carbono (CO2), el metano (CH4) y el óxido nitroso (N2O), tienen la capacidad de absorber y emitir radiación infrarroja, lo que contribuye al efecto invernadero y al calentamiento global. Las actividades humanas, como la quema de combustibles fósiles y la deforestación, pueden aumentar la concentración de estos gases en la atmósfera y, por lo tanto, afectar la cobertura infrarroja.
Es importante estudiar y comprender estas variaciones en los factores de cobertura infrarroja para evaluar su impacto en el clima y en el equilibrio energético de la Tierra. Esto nos permite tomar medidas adecuadas para mitigar los efectos del cambio climático y promover prácticas sostenibles.
ID:(7533, 0)
Variación del Factor de cobertura infrarrojo
Ecuación
La variación del factor de cobertura infrarrojo (IR) se asocian a la variación de los gases de invernadero. Estos se miden el $ppm$ (partes por millón) y $ppb$ (partes por billón) que se calculan de la densidad del gas $\rho$ en el aire según
$ppmv =\displaystyle\frac{gas}{10^6 aire}=\displaystyle\frac{V_n}{M_g}\displaystyle\frac{10^{-6}g,gas}{l,aire}$
y
$ppbv =\displaystyle\frac{gas}{10^9 aire}=\displaystyle\frac{V_n}{M_g}\displaystyle\frac{10^{-9}g,gas}{l,aire}$
donde $M_g$ es la masa molar del gas y $V_n$ es el volumen bajo condiciones normales (temperatura $0^{\circ}C$, presión $10^5,Pa$ que es $22.71108,l$).
A modo de ejemplo, si consideramos el actual nivel de $CO_2$ (masa molar $44.0 g/mol$) veremos que la concentración es de $379 ppmv$ (2005) corresponde a $0.736 g/l CO_2$. Para saber cual es la cantidad de $CO_2$ que existe en la atmósfera debemos saber cuantos litros de aire existen. Como la capa en teoría es infinita (cada vez mas diluida pero igualmente existente tenemos un problema definiendo la altura de la capa de aire. Sin embargo si consideramos que por la ley barométrica la presión baja como
$p(z) = p_0 e^{M_agz/RT}$
tenemos en forma análoga para la densidad
$\rho(z) = \rho_0 e^{M_ag z/RT}$
Si se integra esta ecuación en z se observara que la cantidad es tal como que todo el aire se concentrara con densidad de la superficie en una capa de alto
$z_0 =\displaystyle\frac{RT}{M_ag}= 8001.78m$
a temperatura cero. En otras palabras el volumen total de $CO_2$ en la atmósfera se puede calcular de la densidad ya estimada multiplicándola por el volumen de una capa de $8001.78 m$ de alto que se extiende
sobre todo el planeta. Si se asume un radio de la tierra de $6370 km$ y con la densidad de $0.736e-3,g/l$ se obtiene que la capa d altura $8001.78 m$ una masa de $CO_2$ de 3000 Gt $CO_2$.
Como el peso molar del C es de 14 g/mol y el del $CO_2$ es de $44.1 g/mol$ la masa del carbón en la atmósfera es de $3000\cdot 14/44.1$ lo que da $817 Gt C$. La relación entre la concentración y el forzamiento radiativo se puede obtener de la tabla en la próxima pagina. La información que se maneja de los escenarios indica la cantidad de gases agregados a la atmósfera anualmente. En general el forzamiento radiativo FR se relaciona con la variación de la temperatura en la atmósfera con
$\Delta T = \delta T_b - \delta T_t$
es
| $ \Delta T = \lambda FR $ |
donde $\lambda$ es la sensibilidad climática que corresponde a $0.8 Km^2/W$. Para el caso del $CO_2$ podemos considerar el caso del aumento en $13 ppm$ y el forzamiento radiativo de $1.66 W/m^2$.
ID:(7323, 0)
Estimación de variación de cobertura infrarroja (NIR) total
Ecuación
Para obtener la cobertura infrarroja (NIR) total, representada como $\delta\gamma_i$, se deben sumar las contribuciones de cada gas:
| $ \delta\gamma_{i,k} =\displaystyle\frac{ \Delta F_k }{(1- a_a ) I_s }\displaystyle\frac{ \delta c_k }{ c_k }$ |
donde $\alpha_{ij}$ representa la contribución del gas $j$ a la cobertura infrarroja del gas $i$. La suma se realiza sobre todos los gases relevantes.
Por lo tanto, la variación en la cobertura infrarroja total se puede calcular utilizando la fórmula de Kyon:
| $ \delta\gamma_i =\displaystyle\sum_k \delta\gamma_{i,k} $ |
Esta ecuación proporciona la diferencia relativa entre los valores finales e iniciales de la cobertura infrarroja.
Es importante tener en cuenta que estas ecuaciones son una representación simplificada de los procesos involucrados en el cálculo de la cobertura infrarroja total y su variación. Los cálculos reales pueden tener en cuenta factores adicionales y complejidades específicas del sistema o escenario que se está analizando.
ID:(10831, 0)
Estimación de variación de cobertura infrarroja de un gas
Ecuación
El forzamiento radiativo $\Delta F_k$ para el gas de efecto invernadero $k$ contribuye en función de la radiación solar incidente en el planeta, que es igual a la intensidad de insolación $I_s$ multiplicada por $(1-a_a)$, donde $a_a$ es el albedo de la atmósfera.
Al aumentar la concentración $c_k$ en una cantidad $\delta c_k$, el incremento del flujo que incide desde la atmósfera es igual a:
| $ \delta\gamma_{i,k} =\displaystyle\frac{ \Delta F_k }{(1- a_a ) I_s }\displaystyle\frac{ \delta c_k }{ c_k }$ |
ID:(7590, 0)
Forzamiento radiativo de los principales gases
Descripción
En el diagrama se muestra el forzamiento radiativo de los principales gases en la atmósfera:
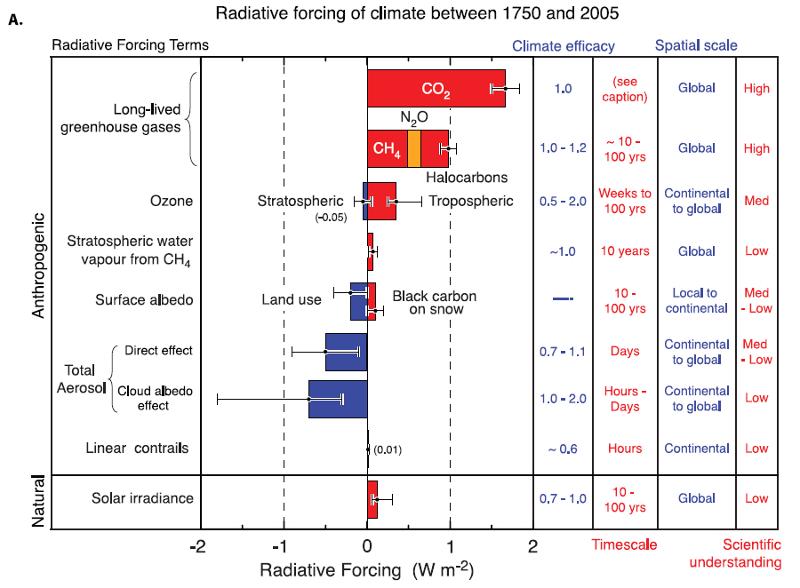
Forzamiento radiativo principales gases
Este diagrama ilustra la contribución relativa de los diferentes gases en el forzamiento radiativo de la atmósfera. Cada gas tiene su propio impacto en el calentamiento o enfriamiento del sistema climático.
Algunos gases, como el dióxido de carbono (CO2) y el metano (CH4), son gases de efecto invernadero que atrapan el calor en la atmósfera y contribuyen al calentamiento global. Otros gases, como el óxido nitroso (N2O), también tienen un efecto de calentamiento.
Por otro lado, algunos gases, como el dióxido de azufre (SO2) y los aerosoles de sulfato, tienen un efecto de enfriamiento al reflejar la radiación solar y reducir la cantidad de energía que llega a la superficie terrestre.
Comprender la importancia relativa de estos gases en el forzamiento radiativo es crucial para evaluar su impacto en el cambio climático y para desarrollar estrategias de mitigación efectivas.
ID:(7325, 0)
Forzamiento radiativo de otros gases y aerosoles
Descripción
El gráfico muestra las formaciones radiativas de otros gases y aerosoles. Algunos de ellos contribuyen a enfriar el planeta:
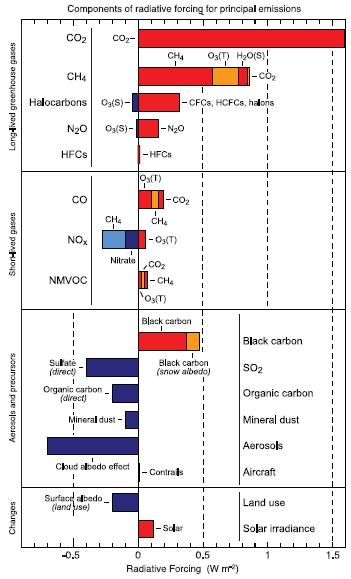
Forzamiento radiativo de otros gases y aerosoles
Estas formaciones radiativas representan la influencia de diferentes gases y aerosoles en el equilibrio energético de la Tierra. Algunos gases, como el dióxido de azufre (SO2) y los aerosoles de sulfato, tienen efectos de enfriamiento al reflejar la radiación solar y reducir la cantidad de radiación que llega a la superficie terrestre.
Es importante comprender la contribución de estos gases y aerosoles en el balance radiativo global, ya que tienen implicaciones significativas en el clima y pueden influir en los patrones climáticos y en el calentamiento global. Estudiar y evaluar su impacto nos permite tomar medidas adecuadas para abordar el cambio climático y buscar soluciones sostenibles.
ID:(7326, 0)
Forzamiento radiativo en el tiempo
Descripción
La gráfica muestra las proyecciones de los cambios radiativos esperados en el horizonte de 20 y 100 años:
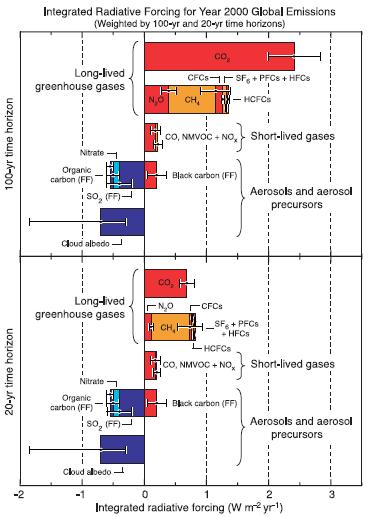
Forzamiento radiativo en el tiempo
Estas proyecciones representan los posibles escenarios de formaciones radiativas en un futuro cercano y lejano. Es importante tener en cuenta que estas proyecciones se basan en modelos y suposiciones científicas actuales y están sujetas a incertidumbres.
El análisis de las formaciones radiativas a largo plazo es esencial para comprender los posibles impactos en el clima y el calentamiento global. Estos resultados pueden ayudar a informar políticas y acciones que busquen mitigar los efectos del cambio climático y promover la sostenibilidad ambiental.
ID:(7327, 0)
Cambios en la atmósfera
Descripción
Una situación que ilustra el impacto de la cobertura en el clima ocurrió durante la prohibición de vuelos comerciales por tres días tras el ataque a las Torres Gemelas. La ausencia de vuelos comerciales durante 72 horas resultó en una disminución de las estelas de condensación (condense triles=contrails), lo que a su vez llevó a un cambio en la cobertura nubosa y a una reducción de las nubes cirrus.
ID:(9247, 0)
Variación de humedad global
Descripción
La variación de la temperatura lleva también a un aumento de la humedad en la atmósfera lo que a su vez afecta el clima.
ID:(93, 0)