Usuario:


Convección
Storyboard

La diferencia de presión atmosférica lleva a desplazamiento de masas de aire tanto a nivel de superficie como en las alturas.

El flujo vertical se denomina convección y es clave para la formación de nubes, generación de lluvias y flujo efectivo de energía entre superficie y atmósfera.

>Modelo

ID:(552, 0)


Convección
Descripción

>Top


Al calentarse una masa de aire esta tiende a dilatarse reduciendose su densidad.

La expansión en si crea una situación en que la presión en su parte superior es menor que en su parte inferior lo que da origen a una diferencia de presión y con ello a una fuerza.

Esta fuerza es analoga a la fuerza de sustentación en el agua, con la diferencia de que con la altura se va reduciendo hasta el punto que ya no supera la gravedad y el cuerpo no continua acendiendo.

ID:(40, 0)


Número de Rayleigh
Ecuación

>Top, >Modelo


El inicio de convección térmica esta descrito por el número de Rayleigh que incluye una serie de parámetros propios del aire y otros geométricos de la situación

$Ra=\displaystyle\frac{\rho^2 g c_p}{\eta\lambda}\displaystyle\frac{(T_e-T_t)}{T_e}h^3$

y que permite determinar cuando la situación se vuelve inestable.

Para un sistema entre dos placas con las temperaturas inferior T_e (superficie de la tierra) y superior T_t (capa superior de la atmósfera) la convección se iniciara al alcanzar un número de Rayleigh de 1708. Para el caso de dos superficies libres el valor crítico es 657.51. Para un sistema de un borde fijo y el otro libre 1,100.65.

En el caso de corrientes aéreas la densidad es \rho\sim 1.27,kg/m^3, capacidad calórica especifica c_p\sim 721.7,J/kg K, conductividad térmica \lambda\sim,0.024,W/m K y viscosidad del aire \eta\sim 1.8\times 10^{-5} Pa,s se obtiene que el numero de Rayleigh es

Ra\sim 2.6\times 10^{10},1/m^3,\displaystyle\frac{(T_e-T_t)}{T_e}h^3

por lo que con el gradiente

\displaystyle\frac{(T_e-T_t)}{T_e}\sim\displaystyle\frac{(14.2-(-30))}{273.15+14.2}\sim 0.16

se concluye que prácticamente siempre de tiene las condiciones para que exista convección.

ID:(9040, 0)


Aerodinámica de la convección
Ecuación

>Top, >Modelo


En general el flujo del aire se puede modelar mediante la ecuación de Navier Stokes

$\rho v\displaystyle\frac{dv}{dx}=(\rho_m-\rho) g$



que en el caso de un flujo unidimensional en una dimensión se puede escribir como

$\rho v\displaystyle\frac{dv}{dx}=(\rho_m-\rho) g$



donde \rho_m es la densidad del medio, \rho la densidad de la masa en ascenso y g la aceleración gravitacional.

Si la velocidad inicial es cero la integración de la ecuación nos dará

$v(z)^2=2g\displaystyle\int_0^zds\displaystyle\frac{(\rho_m(s)-\rho(s))}{\rho(s)}$

ID:(9938, 0)


Ecuación de Navier Stokes
Ecuación

>Top, >Modelo


El flujo de un liquido o gas es descritos mediante la ecuación de Navier Stokes

$\rho\left(\displaystyle\frac{\partial\vec{u}}{\partial t}+\vec{u}\cdot\nabla\vec{u}\right)=-\nabla p+\eta\nabla^2\vec{u}+\displaystyle\frac{1}{3}\nabla(\nabla\cdot\vec{u})+\rho\vec{g}$



que en la aproximación de baja viscosidad, una situación que se puede modelar dimensional y es un flujo estacionario se reduce a

\rho v\displaystyle\frac{dv}{dx}=-\displaystyle\frac{dp}{dx}-\rho g

El gradiente de la presión se modela en este caso con la presión barométrica dando

$\rho v\displaystyle\frac{dv}{dx}=(\rho_m-\rho) g$

ID:(9937, 0)


Velocidad de ascenso
Ecuación

>Top, >Modelo


Para el caso de que la masa de aire asciende en forma lenta la ecuación hidrodinámica de Navier Stokes en una dimensión se puede escribir como

$\rho v\displaystyle\frac{dv}{dx}=(\rho_m-\rho) g$



donde \rho_m es la densidad del medio, \rho la densidad de la masa en ascenso y g la aceleración gravitacional.

Si la velocidad inicial es cero la integración de la ecuación nos dara

$ v(z) ^2 = 2 g \displaystyle\int_0^zds\displaystyle\frac{( \rho_m(s) - \rho(s) )}{ \rho(s) }$

ID:(4869, 0)


CAPE
Ecuación

>Top, >Modelo


Como la densidad es proporcional al inverso de la temperatura

\rho\propto\displaystyle\frac{1}{T}

se tiene que el factor

\displaystyle\frac{\rho_m-\rho}{\rho}

en

$ v(z) ^2 = 2 g \displaystyle\int_0^zds\displaystyle\frac{( \rho_m(s) - \rho(s) )}{ \rho(s) }$



se puede reemplazar por

\displaystyle\frac{T-T_m}{T_m}

e introducir

$CAPE=g\displaystyle\int_0^z ds\displaystyle\frac{(T(s)-T_m(s))}{T_m(s)}$

que tiene unidades de energía y corresponde a la energía potencial de convección CAPE.

ID:(9923, 0)


Velocidad de ascenso en función del CAPE
Ecuación

>Top, >Modelo


Con la velocidad de ascenso dada por

$ v(z) ^2 = 2 g \displaystyle\int_0^zds\displaystyle\frac{( \rho_m(s) - \rho(s) )}{ \rho(s) }$



y la definición del CAPE

$CAPE=g\displaystyle\int_0^z ds\displaystyle\frac{(T(s)-T_m(s))}{T_m(s)}$



se tiene que la velocidad de ascenso en función del CAPE es

$ v =\sqrt{2 CAPE }$

ID:(8836, 0)


Energía potencial de convección
Imagen

>Top


El proceso de convección se describe con el diagrama de presión y temperatura en que se diagraman

- la adiabata de aire seco
- la adiabata de aire humedio
- la temperatura ambiental

y se determina como el volumen evolucionara:

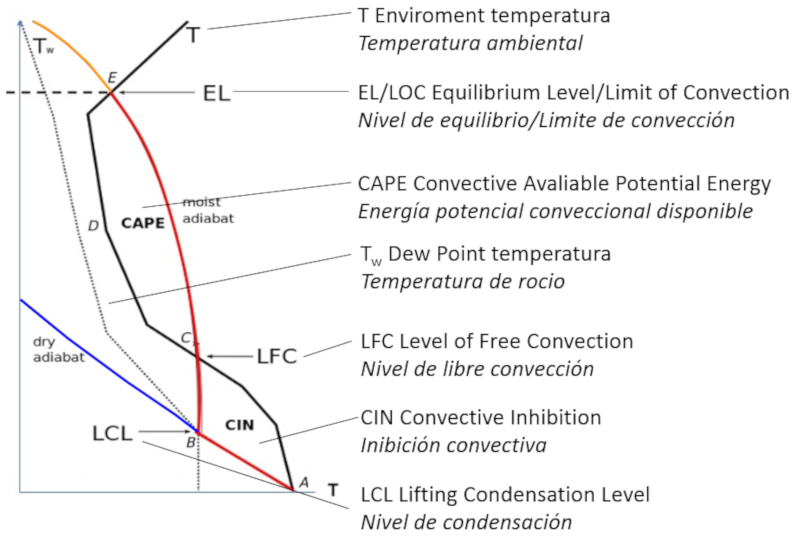
Diagrama de CAPE (Energía potencial de convección disponible)

En el diagrama se muestra como la masa de aire sube:

- sin condesar desde A a B donde inicia la condensación

- comienza a condesar y sube de B a C contra la resistencia CIN

- continua subiendo de C a D impulsado por la energía potencial de condensación

La fase CIN puede evitar que la masa sufra la convección y vuelva a decender.

ID:(3098, 0)


Coeficiente adiabático para aire seco
Ecuación

>Top, >Modelo


Para un proceso adiabático el trabajo es

p,dV=\displaystyle\frac{V,dp}{\gamma}

con \gamma la relación entre calores específicos

\gamma=\displaystyle\frac{c_p}{c_v}

que para un gas ideal es 5/3. De la primera ley de la termodinámica se tiene que

m,c_vdT=\displaystyle\frac{V,dp}{\gamma}

Como en el caso de la atmósfera es

dp=-\rho,g,dz=-\displaystyle\frac{m}{V},g,dz

se tiene que el gradiente adiabático es

\Gamma=-\displaystyle\frac{dT}{dz}

para el caso del aire seco es

$\Gamma=\displaystyle\frac{g}{c_p}$

que corresponde a 9.8 C/km.

ID:(9924, 0)


Relación de masas molares vapor de agua con aire
Ecuación

>Top, >Modelo


La relación de masas molares del vapor de agua con el aire se define como la relación de las masas molares de cada componente presentes en un volumen:

$\zeta=\displaystyle\frac{M_{mol,v}}{M_{mol,a}}$

Como los valores son fijos se puede estimar el valor, el que resulta ser igual a \zeta=0.625.

ID:(9925, 0)


Relación de mezcla de vapor de agua con aire
Ecuación

>Top, >Modelo


La relación de mezcla del vapor de agua con el aire se define como la relación de las masas de cada componente presentes en un volumen:

$\displaystyle\frac{M_v}{M_a}=\displaystyle\frac{n_vM_{mol,v}}{n_aM_{mol,a}}=\displaystyle\frac{p_v}{p_a}\displaystyle\frac{M_{mol,v}}{M_{mol,a}}\sim 0.01$



Donde $M_v$ y $M_a$ son las masas de vapor de agua y aire respectivamente, $n_v$ y $n_a$ son las moles de vapor de agua y aire, $M_{mol,v}$ y $M_{mol,a}$ son las masas molares de vapor de agua y aire, $p_v$ y $p_a$ son las presiones relativas de vapor de agua y aire, y $r$ es la relación de mezcla. Por ello se tiene que es

$ r =\displaystyle\frac{ M_v }{ M_a }$

$M_{m,v}$
Masa molar del agua
$kg/mol$
8060
$M_{m,a}$
Masa molar del aire
$kg$
8059
$r_s$
Relación de masas
$-$
8058

En el caso específico del vapor de agua en el aire, la relación de mezcla es proporcional a las presiones relativas, que se pueden cuantificar utilizando la presión de vapor de agua $p_v\sim 1500 Pa$ y la presión del aire $p_a\sim 10^5 Pa$. Al aplicar la ecuación de los gases y la definición de la masa molar, se obtiene que la relación de mezcla es aproximadamente $0.01$. Esto significa que la cantidad de vapor de agua en comparación con el aire es baja en condiciones normales.

ID:(7069, 0)


Relación de mezcla de vapor de agua con aire en moles
Ecuación

>Top, >Modelo


Con la relación de mezcla de vapor de agua en función de la masa:

$ r =\displaystyle\frac{ M_v }{ M_a }$



la relación entre moles y masas

$ n = \displaystyle\frac{ M }{ M_m }$



y la relación entre masas molares

$\zeta=\displaystyle\frac{M_{mol,v}}{M_{mol,a}}$



se obtiene la relación de mezcla de vapor de agua con aire en función de los moles

$\displaystyle\frac{n_v}{n_a}=\displaystyle\frac{r}{\zeta}$

ID:(9933, 0)


Variaciones de calor para aire húmedo
Ecuación

>Top, >Modelo


La variación del calor esta para aire seco:

$ \Delta Q = C_p \Delta T $



Para el caso de aire húmedo debe considerarse también la masa del vapor de agua. Como la proporción de masa es

$ r =\displaystyle\frac{ M_v }{ M_a }$



se tiene que la masa se puede escribir como

M=M_a(1+r)

donde M_a la masa del aire y con ello

$ \delta Q = M_a(1+ r ) c_p dT $

ID:(9927, 0)


Variaciones de trabajo para aire húmedo
Ecuación

>Top, >Modelo


La variación del trabajo esta para aire seco:

$ \delta W = p dV $



Para el caso de aire húmedo debe considerarse los moles del vapor de agua. Con la ecuación de los gases

$ p V = n R T $



se puede definir el numero total de moles en función de los moles del aire

n=n_a+n_v=n_a\left(1+\displaystyle\frac{n_v}{n_a}\right)=n_a\left(1+\displaystyle\frac{M_v}{M_{mol,v}}\displaystyle\frac{M_{mol,a}}{M_a}\right)=n_a\left(1+\displaystyle\frac{r}{\zeta}\right)

con lo que la ecuación de estado es

$\delta W=-\left(1+\displaystyle\frac{r}{\zeta}\right)n_aRT\displaystyle\frac{dV}{V}$

ID:(9928, 0)


Variaciones de temperatura y volumen para aire húmedo
Ecuación

>Top, >Modelo


En el caso del proceso adiabatico

$ \delta Q =0$



Como el calor es para el caso de aire húmedo es:

$ \delta Q = M_a(1+ r ) c_p dT $



y el trabajo

$\delta W=-\left(1+\displaystyle\frac{r}{\zeta}\right)n_aRT\displaystyle\frac{dV}{V}$



se obtiene con

$ \kappa \equiv1+\displaystyle\frac{ R }{ M_m c_V }$



se obtiene la ecuación de estado

$\displaystyle\frac{dT}{T}=-\displaystyle\frac{(1+r/\zeta)}{(1+r)}(\kappa-1)\displaystyle\frac{dV}{V}$

Al ser r\sim 0.01 el efecto del vapor de agua es me menor orden en la medida que este no se encuentre en estado saturado ya que en dicha situación un cambio de temperatura lleva a condensación o evaporación que si afecta el calor del sistema.

ID:(9926, 0)


Variación del vapor por condensación
Ecuación

>Top, >Modelo


En el caso de que el aire esta saturado, la presión del vapor de agua es:

$ p_s = p_{ref} e^{- l_m / R T }$



y con la ecuación de los gases expresada en función de la concentración

$ p = c_m R T $



se obtiene que

c_s=\displaystyle\frac{p_0e^{-l_m/RT}}{RT}

Si la temperatura varia en una pequeña cantidad dT se puede desarrollar la expresión en la temperatura dando la variación de la concentración en primera aproximación

dc_s=c_s\displaystyle\frac{l_m-RT}{RT^2}dT

Como el calor latente del agua es del orden de l_m\sim 40.65,kJ/mol que es mucho mayor que el factor RT por lo que la variación de la concentración se puede aproximar por

$dc_s=c_s\displaystyle\frac{l_m}{RT^2}dT$

ID:(9929, 0)


Variación del vapor por condensación en función de la masa
Ecuación

>Top, >Modelo


Como la concentración varia con la temperatura en primer orden como:

$dc_s=c_s\displaystyle\frac{l_m}{RT^2}dT$



y la concentración se define como

$ c_m \equiv\displaystyle\frac{ n }{ V }$



se concluye con

$ n = \displaystyle\frac{ M }{ M_m }$



que la variación de la masa es

$dM_s=M_s\displaystyle\frac{l_m}{RT^2}dT$

ID:(9934, 0)


Factor de mezcla para el caso saturado
Ecuación

>Top, >Modelo


Al estar saturado el ractor de mezcla

$ r =\displaystyle\frac{ M_v }{ M_a }$



se debe calcular con la masa saturada que se puede obtener de la concentración saturada multiplicando por el volumen y la masa molar

M_s=VM_{mol,v}c_s=\displaystyle\frac{M_{mol,v}V p_0}{RT}e^{-l_m/RT}

Como por el otro lado la masa del aire es

M_a=M_{mol,a}n_a=\displaystyle\frac{M_{mol,a}p_a V}{RT}

se obtiene que la relación de mezclado del vapor de agua saturado es

$r_s=\zeta_s\displaystyle\frac{p_0}{p_a}e^{-l_m/RT}$

ID:(9935, 0)


Variaciones de calor para aire saturado
Ecuación

>Top, >Modelo


La variación del calor esta para aire seco:

$ \Delta Q = C_p \Delta T $



Para el caso de aire saturado debe considerarse que la variación del vapor de agua lleva al aumento de la masa saturada la que aumenta según

$dM_s=M_s\displaystyle\frac{l_m}{RT^2}dT$



y que entrega el calor que se obtiene multiplicando este valor por el calor latente l_m

l_mdM_s=M_s\displaystyle\frac{l_m^2}{RT^2}dT

Como ademas la masa del vapor de agua se puede relacionar con la masa de aire por la relación de mezcla

$ r =\displaystyle\frac{ M_v }{ M_a }$



se concluye que el calor se modifica con la variación de la temperatura como

$\delta Q = M_a\left(c_p+\displaystyle\frac{l_m^2r_s}{RT^2}\right)dT$



donde la relación de mezcla es

$r_s=\zeta_s\displaystyle\frac{p_0}{p_a}e^{-l_m/RT}$

ID:(9931, 0)


Variaciones de trabajo para aire saturado
Ecuación

>Top, >Modelo


La variación del trabajo esta para aire seco:

$ \delta W = p dV $



Para el caso de aire saturado debe considerarse que la variación del vapor de agua lleva al aumento de la concentración saturada la que aumenta según

$dc_s=c_s\displaystyle\frac{l_m}{RT^2}dT$



con lo que la ecuación de estado es

$\delta W=-\left(1+\displaystyle\frac{l_mr_s}{RT}\right)n_aRT\displaystyle\frac{dV}{V}$



donde la relación de mezcla es

$r_s=\zeta_s\displaystyle\frac{p_0}{p_a}e^{-l_m/RT}$

ID:(9930, 0)


Variaciones de temperatura y volumen para aire saturado
Ecuación

>Top, >Modelo


En el caso del proceso adiabatico

$ \delta Q =0$



Como el calor es para el caso de aire húmedo es:

$\delta Q = M_a\left(c_p+\displaystyle\frac{l_m^2r_s}{RT^2}\right)dT$



y el trabajo

$\delta W=-\left(1+\displaystyle\frac{l_mr_s}{RT}\right)n_aRT\displaystyle\frac{dV}{V}$



se obtiene con

$ \kappa \equiv1+\displaystyle\frac{ R }{ M_m c_V }$



se obtiene la ecuación de estado

$\displaystyle\frac{dT}{T}=-\displaystyle\frac{\left(1+\displaystyle\frac{l_mr_s}{RT}\right)}{\left(1+\displaystyle\frac{l_m^2r_s}{c_pRT^2}\right)}(\kappa-1)\displaystyle\frac{dV}{V}$

Si se evalua el factor que se antepone a el factor (\kappa-1) se ve que su valor es del orden de 0.55 y que es en primer orden independiente de la temperatura. Con ello se puede definir un indice adiabatico para aire saturado con un valor del orden de \kappa_s\sim 1.22 en vez de los tradicionales 1.4.

ID:(9932, 0)


Coeficiente adiabático para aire saturado
Ecuación

>Top, >Modelo


Para el caso del aire no saturado el gradiente adiabático era

$\Gamma=\displaystyle\frac{g}{c_p}$



que con la ecuación del proceso adiabatico saturado

$\displaystyle\frac{dT}{T}=-\displaystyle\frac{\left(1+\displaystyle\frac{l_mr_s}{RT}\right)}{\left(1+\displaystyle\frac{l_m^2r_s}{c_pRT^2}\right)}(\kappa-1)\displaystyle\frac{dV}{V}$



con lo que el coeficiente adiabático para aire saturado es

$\Gamma=\displaystyle\frac{g}{c_p}\displaystyle\frac{1+\displaystyle\frac{l_mr_s}{RT}}{1+\displaystyle\frac{l_m^2r_s\epsilon}{c_pRT^2}}$

El valor se puede representar como el coeficiente adiabático no saturado multiplicado por un coeficiente que es del orden de 0.55. De esta forma el coeficiente adiabático de aire saturado es del orden de 5.4 C/km.

ID:(3097, 0)