Usuario:
Glaciares
Descripción 
Los glaciares constituyen excelentes medios para detectar y estudiar los cambios climáticos.
Ellos constituyen una importante reserva y mecanismo de regulación de la disponibilidad de agua dulce. Por ello su reducción, o incluso desaparición, puede llevar a grandes problemas para zonas urbanas que de ellos dependen. Un ejemplos son las ciudades del norte de Chile, incluyendo Santiago.
Adicionalmente permiten visualizar en forma simple los efectos del cambio climático. esto constituye una buena herramienta de divulgación.
ID:(95, 0)
Análisis de retroceso en Chile (1842-2004)
Imagen
Glaciar Cipreses (Cuenca del Cachapoal):
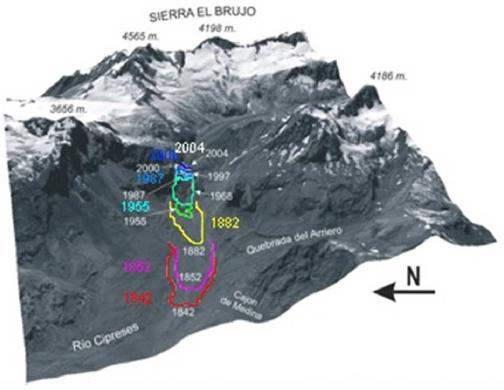
Variación entre 1842 y 2004
ID:(7410, 0)
Retroceso de glaciares en los Alpes
Imagen
El cartel en los Alpes indica que el glaciar en 1990 llegaba hasta este punto y ya tenia un retiro de 1687 metros desde 1900. En la lejanía se observa la posición actual mostrando que el retiro se ha vuelto aun más dramático (fecha desconocida, probablemente fines del 2000):
Reducción de glaciares en los Alpes
ID:(7405, 0)
Comparación glaciares en Austria (1900-2000)
Imagen
Glaciar Pasterze con Großglockner (3798 metros sobre el nivel del mar):
Comparación entre 1900 y 2000
ID:(7407, 0)
Comparación glaciares en Austria (1904-2000)
Imagen
Glaciar Gepatschferner:
Comparación entre 1904 y 2000
ID:(7409, 0)
Comparación glaciares en Austria (1940-2000)
Imagen
Glaciar Pasterze con Großglockner (3798 metros sobre el nivel del mar) y Johannisberg (3467 metros sobre el nivel del mar):
Comparación entre 1940 y 2000
ID:(7406, 0)
Comparación glaciares en Suiza (1940-2000)
Imagen
Glaciar Rhone (Rodano) con Hotel Belvedere (2274 metros sobre el nivel del mar):
Comparación entre 1940 y 2000
ID:(7408, 0)
Variaciones en el Artico
Imagen
El deshielo del artico ha sido dramatico a principio del siglo 21 lo que se ve en los diagramas de cobertura de 2003, 2007 y 2010:
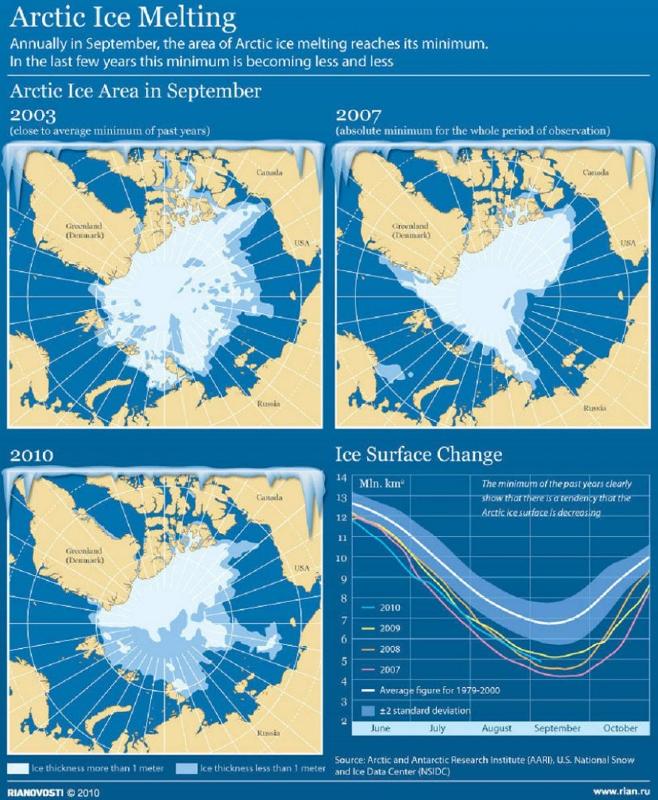
Cobertura del Artico
ID:(7430, 0)
Adelgazamiento de glaciares
Imagen
Desde mediados del siglo pasado se ha comenzado a estudiar y registrar el balance de masa de una serie de glaciares, observándose un adelgazamiento que se estaría acelerando en los últimos años:
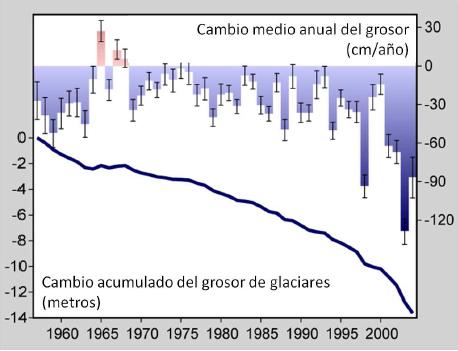
Adelgazamiento medio de glaciares\\n(Datos reportados por WGMS y NSIDC. Grafica sacada de http://www.wikiwand.com/)
Si en el pasado se tenían reducciones de unos 30 cm/año hoy son aproximadamente tres veces mas. El adelgazamiento acumulada (curva continua) llega a mostrar que desde 1950 se tiene la perdida de 14 metros.
ID:(7404, 0)
Variaciones Groenlandia y Antartica
Imagen
En los grandes casquetes de hielo este se reduce hasta en 1.5 metros por año (y en otros aumenta 0.5 metros por año):
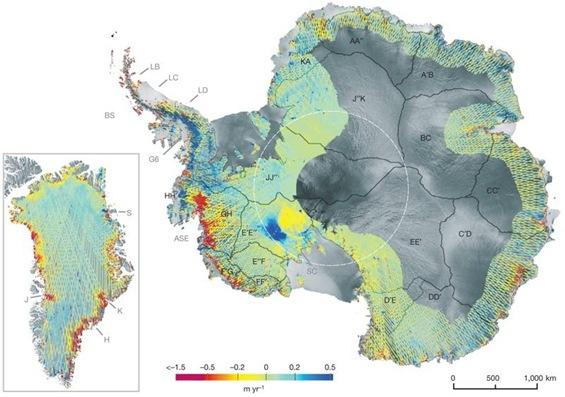
Variaciones Groenlandia y Antártica\\nPritchard, H.D., R.J. Arthern, D.G. Vaughan, and L.A. Edwards. 2009. Extensive dynamic thinning on the margins of the Greenland and Antarctic ice sheets. Nature 461, 971-975.
ID:(7425, 0)
Dinámica de adelgazamiento
Imagen
El sol irradia con una intensidad
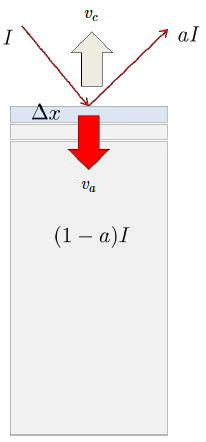
Proceso de ablación y acumulación\\n
El balance de ambas tasas lleva a una modificación de la altura del glaciar que se puede describir mediante una taza de balance de masa y que corresponde a la diferencia de las anteriores.
ID:(7411, 0)
Taza de ablación
Ecuación
Para calcular la tasa de ablación (velocidad de derretimiento), asumiremos que el glaciar tiene una altura h y que está a una temperatura $\Delta T$ menor que el punto de fusión. La energía captada por una capa de altura $\Delta x$ se conduce en parte al interior del glaciar, contribuyendo al derretimiento de la capa y a su calentamiento. Si l es el calor latente y $\rho_e$ la densidad del hielo, un elemento de volumen con superficie $S$ y altura $\Delta x$ requerirá de la energía
$\Delta Ql = S\Delta x l \rho_e$
para fundirse.
Para calentarla a la temperatura de fusión $\Delta T_m$, se necesitará
$\Delta Q_c = S\Delta x\rho_ec\Delta T_m$
donde c es el calor específico. Finalmente, la conducción térmica eliminará calor
$\Delta Q_{\lambda}=\displaystyle\frac{\lambda S\Delta T_b}{h}\Delta t$
donde $\lambda$ es la conductividad térmica, $\Delta T_b$ es la diferencia de temperatura superficie-base y $\Delta t$ es el tiempo transcurrido.
El calor total será, por lo tanto
$\Delta Q_l + \Delta Q_c + \Delta Q_{\lambda} = (1 - a_{ev})(1 - \gamma_v)S I_s\Delta t$
que tras reemplazar por las expresiones resulta en
$S\Delta xl\rho_e + S\Delta x\rho_ec\Delta T_m + (\lambda/h)S \Delta T_b \Delta t = (1 - a_{ev})(1 - \gamma_v)S I_s\Delta t$
Despejando
 $ v_a =\displaystyle\frac{(1 - a_{ev} )(1 - \gamma_v ) I_s - ( \lambda / h ) \Delta T_b }{ \rho_e (l + c \Delta T_m )}$ |
Por lo tanto, un aumento de la temperatura conduce a un aumento de la tasa de ablación.
ID:(7432, 0)
Tasa de acumulación
Ecuación
La tasa de acumulación, denotada como
| $ v_c =\displaystyle\frac{ \Delta x }{ \Delta t }$ |
ID:(7612, 0)
Tasa de balance de masa
Ecuación
La radiación solar se refleja parcialmente y se absorbe en parte por la superficie. Si $I_s$ es el flujo de radiación, $a_{ev}$ es el albedo visible de la Tierra y $\gamma_v$ es el factor de cobertura, la fracción absorbida es
$(1 - a_{ev})(1 -\gamma_v)I_s$
El calor proporcionado se conduce en parte hacia el interior del glaciar y en parte contribuye a derretir una capa de espesor $\Delta x$ en un tiempo $\Delta t$.
De esta manera, la superficie del glaciar se reduciría a una tasa de ablación (velocidad de derretimiento)
$v_a =\displaystyle\frac{\Delta x}{\Delta t}$
debido al efecto de derretimiento, mientras que crecería a una tasa de acumulación $v_c$ (velocidad de deposición de nieve) debido al efecto de la nieve que se deposita en su superficie. Por lo tanto, se produciría una fusión si la velocidad total
| $ v_b = v_c - v_a$ |
resulta ser negativa.
ID:(7434, 0)
Variación de la altura del glaciar
Ecuación
La taza de balance de masa que se calcula de la taza de acumulación y la taza de ablación
| $ v_b = v_c - v_a$ |
permite estimar la variación en la altura especifica del glaciar (en un lugar en particular)
| $\Delta h=v_b\Delta t$ |
ID:(8249, 0)