Écoulement intérieur et érosion
Storyboard 
Le flux interne se produit à travers les capillaires formés entre les particules du sol. Chaque fois que ces capillaires ont des dimensions plus grandes que celles des petites plaques d'argile, il y a un risque que ces particules d'argile soient emportées par ce flux. Si cela se produit, le sol pourrait perdre une partie de sa teneur en argile, ce qui aurait un impact sur ses propriétés mécaniques, sa stabilité et son soutien à la vie organique.
ID:(379, 0)
Débit selon l'équation de Hagen-Poiseuille
Concept 
Le profil de a vitesse dans un rayon du cylindre ($v$) en le rayon de position dans un tube ($r$) nous permet de calculer le volumique flux ($J_V$) dans un tube en intégrant sur toute la surface, ce qui nous conduit à la loi bien connue de Hagen-Poiseuille.
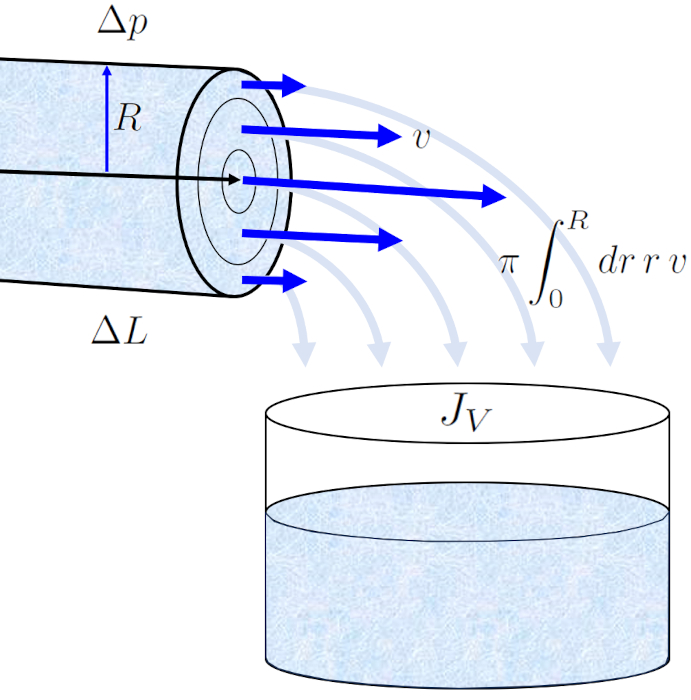
Le résultat est une équation qui dépend de ERROR:5417,0 élevé à la quatrième puissance. Cependant, il est essentiel de noter que ce profil d'écoulement n'est valable que dans le cas d'un écoulement laminaire.
Ainsi, avec cela, on déduit de a viscosité ($\eta$) que le volumique flux ($J_V$) devant un longueur du tube ($\Delta L$) et ERROR:6673,1, l'expression :
| $ J_V =-\displaystyle\frac{ \pi R ^4}{8 \eta }\displaystyle\frac{ \Delta p }{ \Delta L }$ |
Les articles originaux qui ont donné naissance à cette loi avec un nom combiné étaient:![]() "Ueber die Gesetze, welche des der Strom des Wassers in röhrenförmigen Gefässen bestimmen" (Sur les lois régissant l'écoulement de l'eau dans des récipients cylindriques), Gotthilf Hagen, Annalen der Physik und Chemie 46:423442 (1839).
"Ueber die Gesetze, welche des der Strom des Wassers in röhrenförmigen Gefässen bestimmen" (Sur les lois régissant l'écoulement de l'eau dans des récipients cylindriques), Gotthilf Hagen, Annalen der Physik und Chemie 46:423442 (1839).![]() "Recherches expérimentales sur le mouvement des liquides dans les tubes de très-petits diamètres", Jean-Louis-Marie Poiseuille, Comptes Rendus de l'Académie des Sciences 9:433544 (1840).
"Recherches expérimentales sur le mouvement des liquides dans les tubes de très-petits diamètres", Jean-Louis-Marie Poiseuille, Comptes Rendus de l'Académie des Sciences 9:433544 (1840).
ID:(2216, 0)
Écoulement intérieur et érosion
Modèle 
Le flux interne se produit à travers les capillaires formés entre les particules du sol. Chaque fois que ces capillaires ont des dimensions plus grandes que celles des petites plaques d'argile, il y a un risque que ces particules d'argile soient emportées par ce flux. Si cela se produit, le sol pourrait perdre une partie de sa teneur en argile, ce qui aurait un impact sur ses propriétés mécaniques, sa stabilité et son soutien à la vie organique.
Variables
Calculs
Calculs
Équations
Une autre quation utile est celle correspondant la conservation de l' nergie, qui s'applique dans les cas o la viscosit , un processus entra nant une perte d' nergie, peut tre n glig e. Si l'on consid re l' quation classique de l' nergie $E$, qui prend en compte l\' nergie cin tique, l\' nergie potentielle gravitationnelle et une force externe d pla ant le liquide sur une distance $\Delta z$, on peut l\'exprimer de la mani re suivante :
$E=\displaystyle\frac{m}{2}v^2+mgh+F\Delta x$
Si l\'on consid re l\' nergie l\'int rieur d\'un volume $\Delta x\Delta y\Delta z$, on peut remplacer la masse par :
$m=\rho \Delta x\Delta y\Delta z$
Et puisque la pression est donn e par :
$F=p \Delta S =p \Delta y\Delta z$
On obtient l\' quation de la densit d\' nergie :
| $ e =\displaystyle\frac{1}{2} \rho v ^2+ \rho g h + p $ |
(ID 3159)
Quand une a différence de pression ($\Delta p_s$) agit sur une section avec une aire de $\pi R^2$, avec le rayon du tube ($R$) comme le rayon de courbure ($r$), elle g n re une force repr sent e par :
$\pi r^2 \Delta p$
Cette force pousse le liquide contre la r sistance visqueuse, donn e par :
En galant ces deux forces, nous obtenons :
$\pi r^2 \Delta p = \eta 2\pi r \Delta L \displaystyle\frac{dv}{dr}$
Ce qui nous conduit l' quation :
$\displaystyle\frac{dv}{dr} = \displaystyle\frac{1}{2\eta}\displaystyle\frac{\Delta p}{\Delta L} r$
Si nous int grons cette quation d'une position d finie par le rayon de courbure ($r$) jusqu'au bord o se trouve le rayon du tube ($R$) (en tenant compte que la vitesse au bord est nulle), nous pouvons obtenir a vitesse dans un rayon du cylindre ($v$) en fonction de le rayon de courbure ($r$) :
O :
est a vitesse maximal ($v_{max}$) au centre de l' coulement.
(ID 3627)
Si nous supposons que a densité d'énergie ($e$) est conserv , alors pour une cellule o la vitesse moyenne est a vitesse dans un rayon du cylindre ($v$), la densit est a densité ($\rho$), la pression est a pression de la colonne d'eau ($p$), la hauteur est a hauteur de la colonne ($h$), et l'acc l ration gravitationnelle est a accélération gravitationnelle ($g$), nous avons ce qui suit :
| $ e =\displaystyle\frac{1}{2} \rho v ^2+ \rho g h + p $ |
En un point 1, cette quation sera gale la m me quation en un point 2 :
$e(v_1,p_1,h_1)=e(v_2,p_2,h_2)$
o a vitesse moyenne du fluide au point 1 ($v_1$), a hauteur ou profondeur 1 ($h_1$) et a pression dans la colonne 1 ($p_1$) repr sentent la vitesse, la hauteur et la pression au point 1, respectivement, et a vitesse moyenne du fluide au point 2 ($v_2$), a hauteur ou profondeur 2 ($h_2$) et a pression dans la colonne 2 ($p_2$) repr sentent la vitesse, la hauteur et la pression au point 2, respectivement. Par cons quent, nous avons :
| $\displaystyle\frac{1}{2} \rho v_1 ^2+ \rho g h_1 + p_1 =\displaystyle\frac{1}{2} \rho v_2 ^2+ \rho g h_2 + p_2 $ |
(ID 4504)
Dans le cas o il n'y a pas de pression hystrostatique, la loi de Bernoulli pour a densité ($\rho$), a pression dans la colonne 1 ($p_1$), a pression dans la colonne 2 ($p_2$), a vitesse moyenne du fluide au point 1 ($v_1$) et < var>5416
| $\displaystyle\frac{1}{2} \rho v_1 ^2 + p_1 =\displaystyle\frac{1}{2} \rho v_2 ^2 + p_2 $ |
peut tre r crit avec ERROR:6673
| $ dp = p - p_0 $ |
et en gardant l'esprit que
$v_2^2 - v_1^2 = \displaystyle\frac{1}{2}(v_2-v_1)(v_1+v_2)$
avec
| $ \bar{v} = \displaystyle\frac{ v_1 + v_2 }{2}$ |
et
| $ \Delta v = v_2 - v_1 $ |
il faut que
| $ \Delta p = - \rho \bar{v} \Delta v $ |
(ID 4835)
Exemples
Le profil de a vitesse dans un rayon du cylindre ($v$) en le rayon de position dans un tube ($r$) nous permet de calculer le volumique flux ($J_V$) dans un tube en int grant sur toute la surface, ce qui nous conduit la loi bien connue de Hagen-Poiseuille.

Le r sultat est une quation qui d pend de ERROR:5417,0 lev la quatri me puissance. Cependant, il est essentiel de noter que ce profil d' coulement n'est valable que dans le cas d'un coulement laminaire.
Ainsi, avec cela, on d duit de a viscosité ($\eta$) que le volumique flux ($J_V$) devant un longueur du tube ($\Delta L$) et ERROR:6673,1, l'expression :
| $ J_V =-\displaystyle\frac{ \pi R ^4}{8 \eta }\displaystyle\frac{ \Delta p }{ \Delta L }$ |
Les articles originaux qui ont donn naissance cette loi avec un nom combin taient:![]() "Ueber die Gesetze, welche des der Strom des Wassers in r hrenf rmigen Gef ssen bestimmen" (Sur les lois r gissant l' coulement de l'eau dans des r cipients cylindriques), Gotthilf Hagen, Annalen der Physik und Chemie 46:423442 (1839).
"Ueber die Gesetze, welche des der Strom des Wassers in r hrenf rmigen Gef ssen bestimmen" (Sur les lois r gissant l' coulement de l'eau dans des r cipients cylindriques), Gotthilf Hagen, Annalen der Physik und Chemie 46:423442 (1839).![]() "Recherches exp rimentales sur le mouvement des liquides dans les tubes de tr s-petits diam tres", Jean-Louis-Marie Poiseuille, Comptes Rendus de l'Acad mie des Sciences 9:433544 (1840).
"Recherches exp rimentales sur le mouvement des liquides dans les tubes de tr s-petits diam tres", Jean-Louis-Marie Poiseuille, Comptes Rendus de l'Acad mie des Sciences 9:433544 (1840).
(ID 2216)
ID:(379, 0)
