Column of water in the sea
Storyboard 
In the case of the ocean, the density of water, depending on its temperature and salinity, varies with depth. For this reason the pressure cannot be calculated with the traditional pressure formula for the water column. It is necessary to consider the effect of the variation in density and calculate by integrating the mass along the column the pressure that occurs at the depth that we wish to estimate.
ID:(1598, 0)
Characterization of the ocean layers
Image 
Ekman's transport causes the boundaries between the surface and deepest layers in the ocean to shift. These are characterized by sudden changes in parameters depending on the temperature. In particular there are changes in:
• Temperature (thermocline)
• Salinity (halocline)
• Density (pycnocline)

ID:(11684, 0)
Column with variable density
Image 
To calculate the pressure under the sea at a given depth, one must first estimate the mass of a volume element at a certain depth:
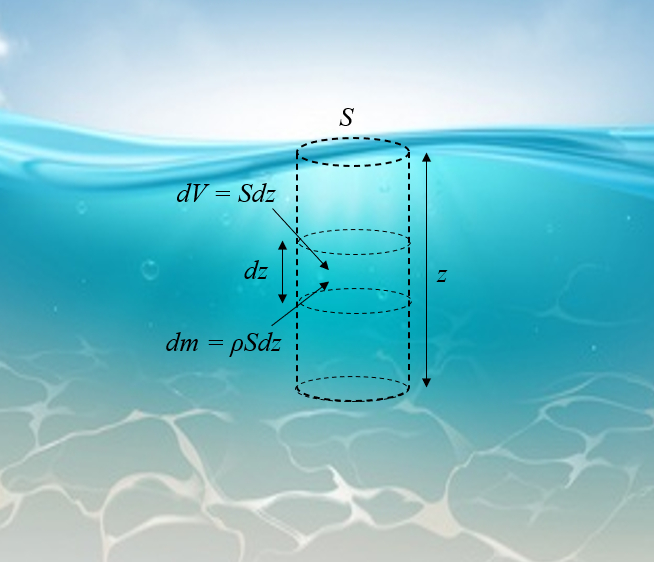
The problem in this case is that the density is not constant so the typical relationship of the pressure of the water column cannot be applied.
ID:(12008, 0)
Mass element
Equation 
A water element of a height
| $ dm = \rho S dz $ |
ID:(12010, 0)
Force element
Equation 
Con la definición de la fuerza gravitacional
| $ F_g = m_g g $ |
el aumento de la fuerza en función de la masa es
| $ dF = g \, dm $ |
ID:(12012, 0)
Variation of force with depth
Equation 
Con la variación de la masa
| $ dm = \rho S dz $ |
y la variación de la fuerza en función de la masa
| $ dF = g \, dm $ |
con lo que se obtiene
| $ dF = \rho g S dz $ |
ID:(12009, 0)
Pressure element
Equation 
Con la definición de la presión
| $ p \equiv\displaystyle\frac{ F }{ S }$ |
la presión aumenta con la fuerza según
| $ dp =\displaystyle\frac{ dF }{ S }$ |
en donde se asume que la sección no varia.
ID:(12013, 0)
Pressure increase ratio with depth
Equation 
Con la definición de la presión
| $ dF = \rho g S dz $ |
el aumento de la fuerza
| $ dp =\displaystyle\frac{ dF }{ S }$ |
lleva a un aumento de la presión
| $ dp = \rho g dz $ |
ID:(12011, 0)
Density modeling
Image 
If you look at the curve of the density of ocean water as a function of depth, you see that it has the shape of an inverted exponential. In other words, the upper part is allowed to compress, reaching a limit where the weight of the column does not lead to greater compression:
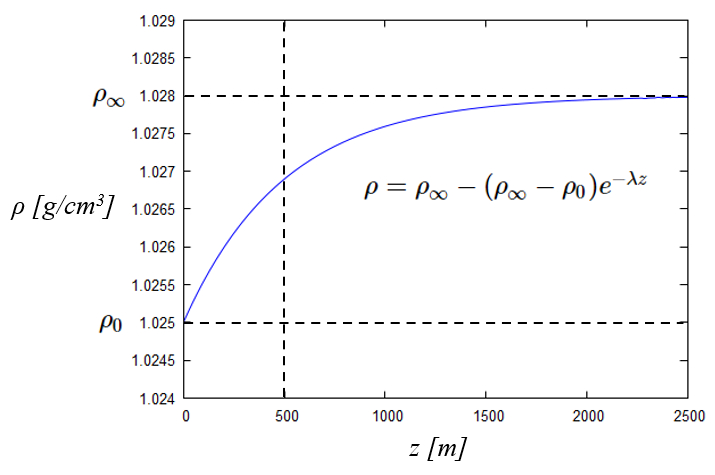
ID:(12014, 0)
Seawater Density Model
Equation 
If you observe the curve of density with depth you can model this with a value for surface density
| $ \rho = \rho_{\infty} - (\rho_{\infty}-\rho_0)e^{-\lambda z }$ |
ID:(11882, 0)
Depth pressure calculation
Equation 
Con el incremento de la presión
| $ dp = \rho g dz $ |
se puede mediante integración calcular la presión para cualquier profundidad:
| $ p = p_0 + g\displaystyle\int_0^z \rho\,du$ |
ID:(11881, 0)
Pressure as a function of depth
Equation 
Si se emplea la función de la densidad
| $ \rho = \rho_{\infty} - (\rho_{\infty}-\rho_0)e^{-\lambda z }$ |
en la ecuación de la presión
| $ p = p_0 + g\displaystyle\int_0^z \rho\,du$ |
se obtiene
| $ p = p_0 + \rho_{\infty} g z - \displaystyle\frac{( \rho_{\infty} - \rho_0 ) g }{ \lambda }(1- e^{- \lambda z })$ |
ID:(11883, 0)
0
Video
Video: Column of water in the sea
