Flutuação
Storyboard 
Quando um corpo está submerso em um meio líquido, ele experimenta a pressão desse meio. Como a pressão aumenta com a profundidade, ela é maior na parte inferior do corpo do que na parte superior, criando uma força dirigida para cima em direção à superfície, conhecida como força de empuxo. Se essa força for maior que a gravidade do corpo, ele subirá até a superfície e flutuará. Se for menor, reduzirá a velocidade com que afunda, mas continuará descendo até tocar o fundo.
ID:(1609, 0)
Flutuação
Storyboard 
Quando um corpo está submerso em um meio líquido, ele experimenta a pressão desse meio. Como a pressão aumenta com a profundidade, ela é maior na parte inferior do corpo do que na parte superior, criando uma força dirigida para cima em direção à superfície, conhecida como força de empuxo. Se essa força for maior que a gravidade do corpo, ele subirá até a superfície e flutuará. Se for menor, reduzirá a velocidade com que afunda, mas continuará descendo até tocar o fundo.
Variáveis
Cálculos
Cálculos
Equações
A press o definida como:
A diferen a de press o :
A se o transversal do corpo multiplicada pela sua altura igual ao seu volume:
Portanto, a for a de empuxo em um corpo submerso :
$F_b = S \Delta p = \rho S \Delta h g = \rho V_s g$
Ou seja:
La força de empuxo ($F_b$) determinada por la densidade líquida ($\rho_w$), o volume deslocado ($V_b$) e la aceleração gravitacional ($g$) como:
o que se op e a la força gravitacional ($F_g$) com la massa de objeto flutuante ($M_s$) segundo:
portanto, com ERROR:8663 e la massa de objeto flutuante ($M_s$),
$F_b = \rho_w V_w g = M_w g = M_s g = F_g$
temos:
Dado que com la massa de objeto flutuante ($M_s$) e ERROR:8663,
relaciona-se com la densidade do objeto ($\rho_s$) e o volume do objeto ($V_s$) por
enquanto v lido que com la densidade líquida ($\rho_w$) e o volume de lastro ($V_w$) temos
obtemos a rela o
Uma vez que o volume deslocado ($V_b$) O volume submerso ($V_s$), mas incluindo o volume de lastro ($V_w$), temos
e a equa o para la densidade líquida ($\rho_w$) representada por
podemos calcular ERROR:8663 como
La força de empuxo ($F_b$) determinado por la densidade líquida ($\rho_w$), o volume deslocado ($V_b$) e la aceleração gravitacional ($g$) como:
o que se op e a la força gravitacional ($F_g$) com la massa de objeto flutuante ($M_s$) como:
Se ambas as for as forem iguais:
o objeto flutuar .
Exemplos
Quando um objeto suspenso em um dinam metro submerso em um l quido, observa-se que a for a indicada por ele diminui, o que indica a exist ncia de uma for a de empuxo uma força de empuxo ($F_b$) gerada pelo l quido.
Quando um objeto flutua, a for a de empuxo la força de empuxo ($F_b$) deve ser igual a la força gravitacional ($F_g$), explicando por que ele n o afunda nem emerge.
Para explicar a sustenta o experimentada por um corpo submerso, necess rio estudar as press es verticais s quais ele est exposto. Como a face inferior do corpo est a uma profundidade maior que a face superior, a press o na parte inferior maior do que na parte superior, resultando em uma for a resultante ascendente que gera a sustenta o observada. Este fen meno semelhante quando um corpo flutua na superf cie, onde n o h press o de gua sobre ele; novamente, a press o na parte inferior que gera sustenta o.
Portanto, no caso em que o corpo est submerso, obtemos:
$\Delta p = p_2 - p_1 = \rho_w g h_2-\rho_w g h_1=\rho_w g (h_2 - h_1) = \rho_w g d$
Ou de forma semelhante na superf cie:
Finalmente, a for a de sustenta o obtida utilizando a defini o de press o, que para la pressão na base ($\Delta p$) com la força de empuxo ($F_b$) e la seção de corpo flutuante ($S_s$) corresponde a:
Um corpo flutua se a for a de empuxo la força de empuxo ($F_b$) for igual ao peso do corpo la força gravitacional ($F_g$):
Isso implica que a rela o entre la massa de objeto flutuante ($M_s$) e ERROR:8663 estabelece:
O que corresponde ao princ pio de Arquimedes [1].
que afirma:
Qualquer objeto flutuante desloca seu pr prio peso em l quido.
![]() [1] "Peri ton Eightumenon" (Sobre corpos flutuantes), Arquimedes, 287 a 212 AC.
[1] "Peri ton Eightumenon" (Sobre corpos flutuantes), Arquimedes, 287 a 212 AC.
Dado que com la massa de objeto flutuante ($M_s$) e ERROR:8663,
relaciona-se com la densidade do objeto ($\rho_s$) e o volume do objeto ($V_s$) por
enquanto v lido que com la densidade líquida ($\rho_w$) e o volume de lastro ($V_w$) temos
obtemos a rela o
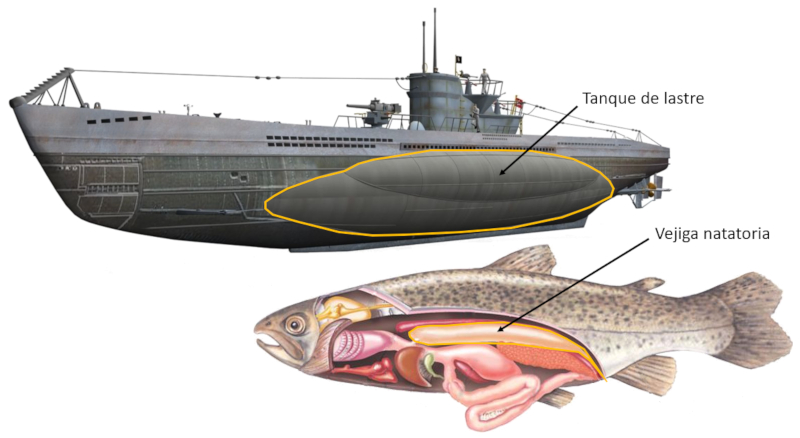
Assim, um objeto com densidade maior que a da gua pode flutuar, desde que tenha um volume de ar abaixo da linha d' gua (superf cie da gua). No caso de um barco, isso corresponde ao espa o ocupado pela carga e/ou passageiros, enquanto em um submarino s o os tanques de lastro e em um peixe a bexiga natat ria.
importante destacar que:
Para um objeto submerso, a suspens o, ascens o ou descida n o dependem da profundidade em que se encontra. No entanto, a capacidade de bombear ar para o tanque de lastro ou bexiga natat ria depende da press o circundante.
A densidade da gua n o homog nea no mar, o que significa que um objeto submerso deve ajustar o volume utilizado no tanque de lastro ou na bexiga natat ria medida que se move.
Submarinos e peixes t m a capacidade de ajustar a profundidade em que permanecem na gua. Eles podem subir superf cie (flutuar) ou descer, limitados apenas pela press o que podem suportar. Isso alcan ado pelo uso de tanques de lastro (em submarinos) e bexigas natat rias (em peixes), que s o espa os nos quais o ar pode se expandir, ocupando um maior volume de gua deslocada.
Para alcan ar isso, a igualdade entre ERROR:8663 e la massa de objeto flutuante ($M_s$) pode ser reescrita em termos de la densidade líquida ($\rho_w$), la densidade do objeto ($\rho_s$) e o volume do objeto ($V_s$), permitindo o ajuste de o volume de lastro ($V_w$):
permitindo que uma seja igual ou exceda a outra. Em resumo, se o volume de lastro ($V_w$) for aumentado, a flutuabilidade aumenta, causando ascens o; reduzindo o volume resulta em descida. Se o volume permanecer o mesmo, eles permanecem suspensos.
Um estudo interessante sobre como as baleias usam o rg o de espermacete para controlar a flutuabilidade por meio de calor e gorduras pode ser encontrado no estudo "Buoyancy Control as a Function of the Spermaceti Organ in the Sperm Whale" de Malcolm R. Clarke, publicado na J.mar.bio.Ass U.K. (1978) 58, 27-71.
La pressão da coluna de água ($p$) calculado a partir de la força da coluna ($F$) e la altura da coluna líquida ($S$) da seguinte forma:
A La pressão na base ($\Delta p$) que existe no plano mais profundo do corpo com o rascunho de objeto ($d$), la densidade líquida ($\rho_w$) e la aceleração gravitacional ($g$) ent o:
La força de empuxo ($F_b$) pode ser expresso em termos de o volume deslocado ($V_b$), la densidade líquida ($\rho_w$) e la aceleração gravitacional ($g$) com:
Nota: O volume considerado aqui o volume submerso. Se o corpo n o estiver completamente submerso, apenas o volume correspondente ao l quido deslocado deve ser considerado.
La força gravitacional ($F_g$) baseia-se em la massa gravitacional ($m_g$) do objeto e em uma constante que reflete a intensidade da gravidade na superf cie do planeta. Esta ltima identificada por la aceleração gravitacional ($g$), que igual a $9.8 m/s^2$.
Consequentemente, conclui-se que:
Se la força gravitacional ($F_g$) for igual a la força de empuxo ($F_b$):
o objeto flutuar .
Se la força de empuxo ($F_b$) e la força gravitacional ($F_g$) forem iguais, o objeto flutuar . Neste caso, isso significa que la massa de objeto flutuante ($M_s$) deve ser igual a ERROR:8663, resultando em:
Nota: esta rela o s poss vel se o objeto 'pesar menos que a gua', o que significa que a gua deslocada ocupa um volume igual ou maior que o do objeto.
Quando um corpo est submerso, o volume de lastro ($V_w$) no tanque de lastro inclu do com o volume do objeto ($V_s$) no total de o volume deslocado ($V_b$). Portanto, temos:
Com o volume da gua deslocada igual soma de o volume de lastro ($V_w$) e o volume submerso ($V_s$), que pode ser calculado com la densidade líquida ($\rho_w$), podemos determinar ERROR:8663:
A condi o float com o volume de lastro ($V_w$), la densidade líquida ($\rho_w$), la densidade do objeto ($\rho_s$) e o volume do objeto ($V_s$):
ID:(1609, 0)