Druyd:Knowledge

Solución de la ecuación de balance

Storyboard

Las ecuaciones para la temperatura de la superficie de la tierra, parte de abajo y parte superior de la atmósfera pueden ser resueltas mediante técnicas de perturbación. Esto es se suponen pequeñas variaciones de la intensidad solar, albedos y factores de cobertura y se estima como estos afectan la variación de dichas temperaturas.

>Modelo

ID:(575, 0)

Fundamentos del modelo

Descripción

Dado que los parámetros del modelo varían poco alrededor de sus valores medios, es posible realizar un desarrollo de Taylor alrededor de dichos valores medios. De esta manera, se obtienen ecuaciones lineales que pueden ser resueltas de forma exacta.

ID:(84, 0)

Modelo básico de flujo radiativo

Imagen

El siguiente diagrama ilustra los flujos radiativos principales (visible e infrarrojo) en un modelo simplificado de la Tierra:

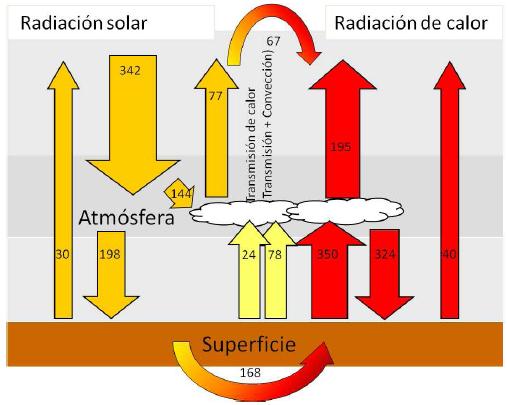
Este diagrama representa de manera simplificada la interacción de la radiación en la Tierra. La radiación visible del sol alcanza la superficie terrestre, donde puede ser reflejada hacia el espacio exterior, absorbida por la superficie terrestre y convertida en radiación infrarroja, o absorbida por la atmósfera. A su vez, la Tierra emite radiación infrarroja hacia el espacio.Estos flujos radiativos son fundamentales para comprender el equilibrio energético de nuestro planeta y los procesos que regulan el clima.

ID:(7331, 0)

Suposición evolución de la sociedad

Descripción

Para simular el desarrollo futuro del clima, se asumieron cuatro posibles escenarios:- A1: Crecimiento económico rápido, el consumo de energía se triplica para el año 2100. Aumento de la población hasta 9 mil millones en 2050 y posterior disminución lenta.- A2: Crecimiento económico moderado, el consumo de energía aumenta gradualmente pero se triplica para el año 2100. Aumento continuo de la población hasta 15 mil millones en 2100.- B1: Crecimiento económico rápido, el consumo de energía disminuye para el año 2100. Aumento de la población hasta 9 mil millones en 2050 y posterior disminución lenta.- B2: Crecimiento económico más lento, el consumo de energía aumenta significativamente pero se estabiliza para el año 2100. Aumento lento de la población hasta 10 mil millones en 2100.En cada uno de estos escenarios se estima:- El consumo de energía y la forma en que se genera.- La producción y el tipo de alimentos consumidos.Además, se estima la generación de los gases correspondientes.

ID:(7324, 0)

Ecuaciones de equilibrio

Descripción

En caso de equilibrio, se cumplen las siguientes tres ecuaciones de equilibrio radiativo:

$(1 - a_a)(1 - \gamma_{\nu})I_s - \kappa (T_e - T_b) - \sigma\epsilon_eT_e^4 + \sigma\epsilon_b T_b^4 = 0$

$\kappa(T_e - T_b) + \gamma_i\sigma\epsilon_e T_e^4 - 2\sigma\epsilon_bT_b^4 = 0$

$(1 - a_a)\gamma_{\nu} + \sigma\epsilon_b T_b^4 - 2\sigma\epsilon_t T_t^4 = 0$

donde $T_e$ es la temperatura de la Tierra, $T_b$ es la temperatura en la parte inferior de la atmósfera y $T_t$ es la temperatura en la parte superior. Además, se tiene que la radiación solar promedio es $I_s$, los albedos de la atmósfera y la Tierra son $a_a$ y $a_e$ respectivamente, $\gamma_{u}$ y $\gamma_i$ son los factores de cobertura en el rango visible e infrarrojo, $\epsilon_e$ y $\epsilon_a$ son las emisividades de la Tierra y la atmósfera, y $\sigma$ es la constante de Stefan-Boltzmann.

ID:(85, 0)

Ecuaciones aproximadas

Descripción

Empleando las aproximaciones, se obtiene para la ecuación que en una aproximación lineal es:

$-\kappa(\delta T_e-\delta T_b)-4\sigma\epsilon_e T_e^3\delta T_e+4\sigma\epsilon_b T_b^3\delta T_b-\delta a_e(1-\gamma_{\nu})I_s-(1-a_e)\delta\gamma_{\nu}I_s=0$

En forma análoga se obtiene para la segunda ecuación la expresión:

$\kappa(\delta T_e-\delta T_b)+\sigma\epsilon_e T_e^4\delta\gamma_i+4\gamma_i\sigma\epsilon_e T_e^3\delta T_e+4\sigma\epsilon_t T_t^3\delta T_t-8\sigma\epsilon_b T_b^3\delta T_b=0$

y para la tercera:

$-2\sigma \epsilon_t T_t^3\delta T_t+\sigma\epsilon_b T_b^3\delta T_b-\gamma_{\nu}I_s\delta a_a+(1-a_a) I_s\delta\gamma_i=0$

Las tres ecuaciones forman un sistema de ecuaciones lineales para calcular las variaciones de las temperaturas $\delta T_e$, $\delta T_b$ y $\delta T_t$ en función de las variaciones de los albedos $\delta a_e$ y $\delta a_a$ y de los factores de cobertura $\delta \gamma_{u}$ y $\delta \gamma_i$.

ID:(87, 0)

Simulador del modelo

Descripción

Las ecuaciones de balance radiativo nos permiten calcular las temperaturas en la superficie de la Tierra $T_e$, en la parte inferior de la atmósfera $T_b$ y en la parte superior $T_t$. Estas ecuaciones se representan de la siguiente manera:

Ecuación 1: El cambio en la temperatura en la superficie de la Tierra se calcula mediante la ecuación

$M_eC_e\displaystyle\frac{dT_e}{dt}=(1-a_e)(1-\gamma_v)I_s-\kappa(T_e-T_b)-\sigma\epsilon T_e^4+\sigma\epsilon T_b^4$

donde $M_e$ es la masa de la Tierra, $C_e$ es la capacidad calorífica de la Tierra, $a_e$ es el albedo de la Tierra, $\gamma_v$ es la fracción de radiación visible absorbida por la atmósfera, $I_s$ es la radiación solar incidente, $\kappa$ es la conductividad térmica, $\sigma$ es la constante de Stefan-Boltzmann y $\epsilon$ es la emisividad de la Tierra.

Ecuación 2: El cambio en la temperatura en la parte inferior de la atmósfera se calcula mediante la ecuación

$M_bC_b\displaystyle\frac{dT_b}{dt}=\kappa(T_e-T_b)+\gamma_i\sigma\epsilon T_e^4-2\sigma\epsilon T_b^4+\sigma\epsilon T_t^4=0$

donde $M_b$ es la masa de la atmósfera, $C_b$ es la capacidad calorífica de la atmósfera y $\gamma_i$ es la fracción de radiación infrarroja absorbida por la atmósfera.

Ecuación 3: El cambio en la temperatura en la parte superior de la atmósfera se calcula mediante la ecuación

$M_tC_t\displaystyle\frac{dT_t}{dt}=(1-a_a)\gamma_vI_s+\sigma\epsilon T_b^4-2\sigma\epsilon T_t^4=0$

donde $M_t$ es la masa de la parte superior de la atmósfera y $C_t$ es la capacidad calorífica de la parte superior de la atmósfera.Estas ecuaciones representan el equilibrio entre la radiación solar incidente, la radiación emitida por la Tierra y la radiación transferida entre las diferentes capas de la Tierra y la atmósfera. Al resolver estas ecuaciones, podemos obtener las temperaturas en cada una de estas capas.

ID:(6867, 0)

Solución numérica

Descripción

El sistema de ecuaciones puede resolverse de forma analítica. Si evaluamos las expresiones para los parámetros de las condiciones actuales de la Tierra ($a_e = 0.152$, $a_a = 0.535$, $\gamma_{
u} = 0.421$, $\gamma_i=0.897$, $\kappa = 2.226 , \text{W/m}^2 \text{K}^{-1}$, $\epsilon_e = \epsilon_b = \epsilon_t = 1$, $I_s = 342 , \text{W/m}^2$, $T_e = 14.8^\circ \text{C}$, $T_b = 1.79^\circ \text{C}$ y $T_t = -30.98^\circ \text{C}$), se obtendría:

$\delta T_e = 0.240\delta I_s - 97.978\delta\gamma_v+123.671\delta \gamma_i - 84.112\delta a_e - 22.827\delta a_a$

$\delta T_b = 0.193\delta I_s - 66.120\delta \gamma_v + 136.209\delta \gamma_i - 64.106\delta a_e - 25.142\delta a_a$

$\delta T_t = 0.172\delta I_s - 23.693\delta \gamma_v + 99.662\delta \gamma_i-46.905\delta a_e - 40.745\delta a_a$

ID:(7319, 0)

Calentamiento Global bajo distintos escenarios

Imagen

Si se consideran los distintos escenarios B1, A1B y A1 se puede estudiar la probable evolución de la temperatura sobre la superficie del planeta.

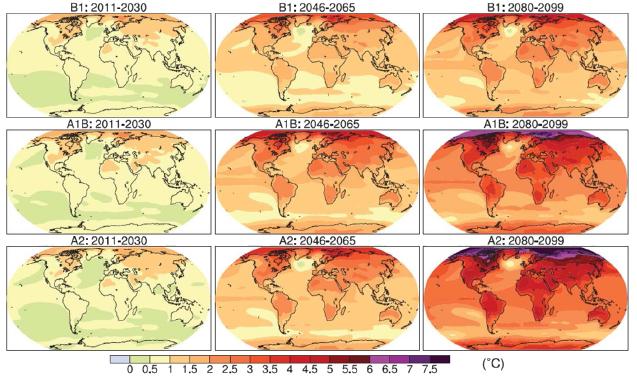
Calentamiento Global bajo distintos escenarios

5.3-------7.67.57.68.27.67.6-8.78.78.711.38.79.3-7.17.17.015.17.010.421-------535657415351-16418118782136110-5255295502433282356.0-------11.212.110.011.010.09.0-23.116.012.316.511.711.2-30.313.14.328.95.213.81.1-------1.50.50.31.20.60.0-0.80.40.00.9-0.4-0.2--2.10.40.00.2-1.0-0.5310-------416421415424377384-630452500598359505-7352892748892365976.7-------9.37.26.19.68.16.1-14.57.46.112.08.36.3-16.67.05.416.55.76.9

Escenarios	1990	A1FI	A1B	A1T	A2	B1	B2
Población (1E+9)
2020
2050
2100
GDP (1E+12 1990US$/yr)
2020
2050
2100
CO2, fosil (GtC/yr)
2020
2050
2100
CO2, agro (GtC/yr)
2020
2050
2100
Metano, (MtCH4/yr)
2020
2050
2100
NO, (MtN/yr)
2020
2050
2100

ID:(7333, 0)

Calentamiento Global (ejemplo)

Imagen

La siguiente gráfica muestra el calentamiento según zona geográfica:

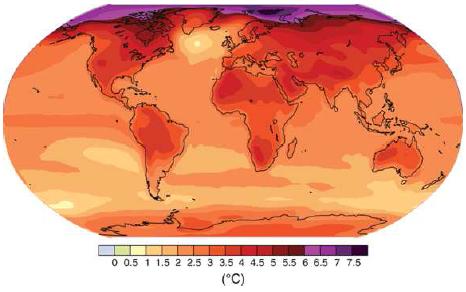
Calentamiento Global (ejemplo)

ID:(7332, 0)

Solución de la ecuación de balance

Modelo

Variables

Símbolo

Texto

Variable

Valor

Unidades

Calcule

Valor MKS

Unidades MKS

$I_s$

I_s

Intensidad de radiación solar

W/m^2

$I_{st}$

I_st

Nueva intensidad de radiación solar

W/m^2

$T_{bt}$

T_bt

Nueva temperatura atmosférica inferior

$T_{tt}$

T_tt

Nueva temperatura atmosférica superior

$T_{et}$

T_et

Nueva temperatura superficie terrestre

$T_b$

T_b

Temperatura de la atmosférica inferior

$T_e$

T_e

Temperatura de la superficie del planeta

$T_t$

T_t

Temperatura en la parte superior de la atmosférica

$\delta\gamma_i$

dgamma_i

Variación de la cobertura infrarroja (NIR)

$\delta\gamma_v$

dgamma_v

Variación de la cobertura visible (VIS)

$\delta I_s$

dI_s

Variación de la intensidad de radiación solar

W/m^2

$\delta T_b$

dT_b

Variación de la temperatura atmosférica inferior

$\delta T_t$

dT_t

Variación de la temperatura atmosférica superior

$\delta T_e$

dT_e

Variación de la temperatura superficie terrestre

$\delta a_a$

da_a

Variación del albedo de la cobertura atmosférica

$\delta a_e$

da_e

Variación del albedo de la superficie terrestre

Cálculos

Ecuación

Número

Primero, seleccione la ecuación:

, luego, seleccione la variable:

Símbolo

Ecuación

Resuelto

Traducido

Cálculos

Símbolo

Ecuación

Resuelto

Traducido

Variable

Dado

Calcule

Objetivo :

Ecuación

A utilizar

Ecuaciones

$\delta T_e = 0.240\delta I_s - 97.978\delta\gamma_v+123.671\delta \gamma_i - 84.112\delta a_e - 22.827\delta a_a$

dT_e = 0.240dI_s - 97.978dg_v +123.671dg_i - 84.112da_e - 22.827da_a

(ID 7440)

$\delta T_b = 0.193\delta I_s - 66.120\delta \gamma_v + 136.209\delta \gamma_i - 64.106\delta a_e - 25.142\delta a_a$

dT_b = 0.193dI_s - 66.120dg_v + 136.209dg_i - 64.106da_e - 25.142da_a

(ID 7441)

$\delta T_t = 0.172\delta I_s - 23.693\delta \gamma_v + 99.662\delta \gamma_i-46.905\delta a_e - 40.745\delta a_a$

dT_t = 0.172dI_s - 23.693dg_v + 99.662dg_i-46.905da_e - 40.745da_a

(ID 7442)

$ I_{st} = I_s + \delta I_s $

I_st = I_s + dI_s

(ID 7604)

$ T_{et} = T_e + \delta T_e $

T_et = T_e + dT_e

(ID 7605)

$ T_{bt} = T_b + \delta T_b $

T_bt = T_b + dT_b

(ID 7606)

$ T_{tt} = T_t + \delta T_t $

T_tt = T_t + dT_t

(ID 7607)

Ejemplos

Fundamentos del modelo

Dado que los par metros del modelo var an poco alrededor de sus valores medios, es posible realizar un desarrollo de Taylor alrededor de dichos valores medios. De esta manera, se obtienen ecuaciones lineales que pueden ser resueltas de forma exacta.

(ID 84)

Modelo b sico de flujo radiativo

El siguiente diagrama ilustra los flujos radiativos principales (visible e infrarrojo) en un modelo simplificado de la Tierra:

Este diagrama representa de manera simplificada la interacci n de la radiaci n en la Tierra. La radiaci n visible del sol alcanza la superficie terrestre, donde puede ser reflejada hacia el espacio exterior, absorbida por la superficie terrestre y convertida en radiaci n infrarroja, o absorbida por la atm sfera. A su vez, la Tierra emite radiaci n infrarroja hacia el espacio.Estos flujos radiativos son fundamentales para comprender el equilibrio energ tico de nuestro planeta y los procesos que regulan el clima.

(ID 7331)

Suposici n evoluci n de la sociedad

Para simular el desarrollo futuro del clima, se asumieron cuatro posibles escenarios:- A1: Crecimiento econ mico r pido, el consumo de energ a se triplica para el a o 2100. Aumento de la poblaci n hasta 9 mil millones en 2050 y posterior disminuci n lenta.- A2: Crecimiento econ mico moderado, el consumo de energ a aumenta gradualmente pero se triplica para el a o 2100. Aumento continuo de la poblaci n hasta 15 mil millones en 2100.- B1: Crecimiento econ mico r pido, el consumo de energ a disminuye para el a o 2100. Aumento de la poblaci n hasta 9 mil millones en 2050 y posterior disminuci n lenta.- B2: Crecimiento econ mico m s lento, el consumo de energ a aumenta significativamente pero se estabiliza para el a o 2100. Aumento lento de la poblaci n hasta 10 mil millones en 2100.En cada uno de estos escenarios se estima:- El consumo de energ a y la forma en que se genera.- La producci n y el tipo de alimentos consumidos.Adem s, se estima la generaci n de los gases correspondientes.

(ID 7324)

Ecuaciones de equilibrio

En caso de equilibrio, se cumplen las siguientes tres ecuaciones de equilibrio radiativo:

$(1 - a_a)(1 - \gamma_{\nu})I_s - \kappa (T_e - T_b) - \sigma\epsilon_eT_e^4 + \sigma\epsilon_b T_b^4 = 0$

$\kappa(T_e - T_b) + \gamma_i\sigma\epsilon_e T_e^4 - 2\sigma\epsilon_bT_b^4 = 0$

$(1 - a_a)\gamma_{\nu} + \sigma\epsilon_b T_b^4 - 2\sigma\epsilon_t T_t^4 = 0$

donde $T_e$ es la temperatura de la Tierra, $T_b$ es la temperatura en la parte inferior de la atm sfera y $T_t$ es la temperatura en la parte superior. Adem s, se tiene que la radiaci n solar promedio es $I_s$, los albedos de la atm sfera y la Tierra son $a_a$ y $a_e$ respectivamente, $\gamma_{u}$ y $\gamma_i$ son los factores de cobertura en el rango visible e infrarrojo, $\epsilon_e$ y $\epsilon_a$ son las emisividades de la Tierra y la atm sfera, y $\sigma$ es la constante de Stefan-Boltzmann.

(ID 85)

Ecuaciones aproximadas

Empleando las aproximaciones, se obtiene para la ecuaci n que en una aproximaci n lineal es:

$-\kappa(\delta T_e-\delta T_b)-4\sigma\epsilon_e T_e^3\delta T_e+4\sigma\epsilon_b T_b^3\delta T_b-\delta a_e(1-\gamma_{\nu})I_s-(1-a_e)\delta\gamma_{\nu}I_s=0$

En forma an loga se obtiene para la segunda ecuaci n la expresi n:

$\kappa(\delta T_e-\delta T_b)+\sigma\epsilon_e T_e^4\delta\gamma_i+4\gamma_i\sigma\epsilon_e T_e^3\delta T_e+4\sigma\epsilon_t T_t^3\delta T_t-8\sigma\epsilon_b T_b^3\delta T_b=0$

y para la tercera:

$-2\sigma \epsilon_t T_t^3\delta T_t+\sigma\epsilon_b T_b^3\delta T_b-\gamma_{\nu}I_s\delta a_a+(1-a_a) I_s\delta\gamma_i=0$

Las tres ecuaciones forman un sistema de ecuaciones lineales para calcular las variaciones de las temperaturas $\delta T_e$, $\delta T_b$ y $\delta T_t$ en funci n de las variaciones de los albedos $\delta a_e$ y $\delta a_a$ y de los factores de cobertura $\delta \gamma_{u}$ y $\delta \gamma_i$.

(ID 87)

Simulador del modelo

Las ecuaciones de balance radiativo nos permiten calcular las temperaturas en la superficie de la Tierra $T_e$, en la parte inferior de la atm sfera $T_b$ y en la parte superior $T_t$. Estas ecuaciones se representan de la siguiente manera:

Ecuaci n 1: El cambio en la temperatura en la superficie de la Tierra se calcula mediante la ecuaci n

$M_eC_e\displaystyle\frac{dT_e}{dt}=(1-a_e)(1-\gamma_v)I_s-\kappa(T_e-T_b)-\sigma\epsilon T_e^4+\sigma\epsilon T_b^4$

donde $M_e$ es la masa de la Tierra, $C_e$ es la capacidad calor fica de la Tierra, $a_e$ es el albedo de la Tierra, $\gamma_v$ es la fracci n de radiaci n visible absorbida por la atm sfera, $I_s$ es la radiaci n solar incidente, $\kappa$ es la conductividad t rmica, $\sigma$ es la constante de Stefan-Boltzmann y $\epsilon$ es la emisividad de la Tierra.

Ecuaci n 2: El cambio en la temperatura en la parte inferior de la atm sfera se calcula mediante la ecuaci n

$M_bC_b\displaystyle\frac{dT_b}{dt}=\kappa(T_e-T_b)+\gamma_i\sigma\epsilon T_e^4-2\sigma\epsilon T_b^4+\sigma\epsilon T_t^4=0$

donde $M_b$ es la masa de la atm sfera, $C_b$ es la capacidad calor fica de la atm sfera y $\gamma_i$ es la fracci n de radiaci n infrarroja absorbida por la atm sfera.

Ecuaci n 3: El cambio en la temperatura en la parte superior de la atm sfera se calcula mediante la ecuaci n

$M_tC_t\displaystyle\frac{dT_t}{dt}=(1-a_a)\gamma_vI_s+\sigma\epsilon T_b^4-2\sigma\epsilon T_t^4=0$

donde $M_t$ es la masa de la parte superior de la atm sfera y $C_t$ es la capacidad calor fica de la parte superior de la atm sfera.Estas ecuaciones representan el equilibrio entre la radiaci n solar incidente, la radiaci n emitida por la Tierra y la radiaci n transferida entre las diferentes capas de la Tierra y la atm sfera. Al resolver estas ecuaciones, podemos obtener las temperaturas en cada una de estas capas.

(ID 6867)

Soluci n num rica

El sistema de ecuaciones puede resolverse de forma anal tica. Si evaluamos las expresiones para los par metros de las condiciones actuales de la Tierra ($a_e = 0.152$, $a_a = 0.535$, $\gamma_{
u} = 0.421$, $\gamma_i=0.897$, $\kappa = 2.226 , \text{W/m}^2 \text{K}^{-1}$, $\epsilon_e = \epsilon_b = \epsilon_t = 1$, $I_s = 342 , \text{W/m}^2$, $T_e = 14.8^\circ \text{C}$, $T_b = 1.79^\circ \text{C}$ y $T_t = -30.98^\circ \text{C}$), se obtendr a:

$\delta T_e = 0.240\delta I_s - 97.978\delta\gamma_v+123.671\delta \gamma_i - 84.112\delta a_e - 22.827\delta a_a$

$\delta T_b = 0.193\delta I_s - 66.120\delta \gamma_v + 136.209\delta \gamma_i - 64.106\delta a_e - 25.142\delta a_a$

$\delta T_t = 0.172\delta I_s - 23.693\delta \gamma_v + 99.662\delta \gamma_i-46.905\delta a_e - 40.745\delta a_a$

(ID 7319)

Calentamiento Global bajo distintos escenarios

Si se consideran los distintos escenarios B1, A1B y A1 se puede estudiar la probable evoluci n de la temperatura sobre la superficie del planeta.

Calentamiento Global bajo distintos escenarios

Escenarios	1990	A1FI	A1B	A1T	A2	B1	B2
Poblaci n (1E+9)
2020
2050
2100
GDP (1E+12 1990US$/yr)
2020
2050
2100
CO2, fosil (GtC/yr)
2020
2050
2100
CO2, agro (GtC/yr)
2020
2050
2100
Metano, (MtCH4/yr)
2020
2050
2100
NO, (MtN/yr)
2020
2050
2100

(ID 7333)

Calentamiento Global (ejemplo)

La siguiente gr fica muestra el calentamiento seg n zona geogr fica:

Calentamiento Global (ejemplo)

(ID 7332)

ID:(575, 0)