Usuario:
Modelo simplificado
Imagen 
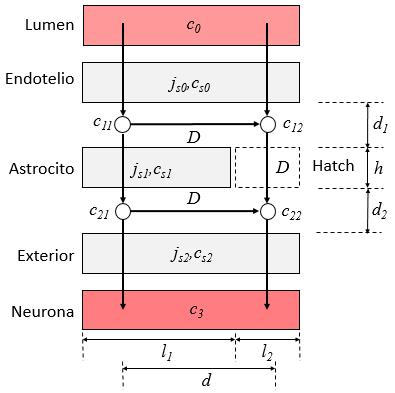
En la medida que la difusión a lo largo del perímetro es menor el sistema se puede modelar con cuatro concentraciones básicas:
- $c_{11}$ en cavidad entre endotelio y membrana laminar
- $c_{12}$ en primera cavidad frente al hatch
- $c_{21}$ en cavidad entre membrana laminar y membrana exterior
- $c_{22}$ en segunda cavidad frente al hatch
Se consideran ademas las dimensiones geométricas:
- $l_1$ perímetro sin el hatch
- $l_2$ ancho del hatch
- $h$ largo del hatch (que es de mayor largo que la membrana)
- $d_1$ ancho primera cavidad
- $d_2$ ancho segunda cavidad
Se incluyen las constantes de difusión
- $D_0$ a través del endotelio
- $D_1$ a través de la membrana laminar
- $D_2$ a través de la membrana exterior
- $D$ a través del medio liquido (perimetral y hatch)
Se asume además de que el sistema no llega al limite de saturación.
ID:(8855, 0)
Simulación básica 0.5 s
Descripción
Si se considera un sistema que inicialmente no tiene glucosa y que esta en contacto con un lumen con 5.5 mmol/l y con un nervio con 0 mmol/l se tienen los datosque en los primeros 0.5 s muestran que las concentraciones en los cuatro puntos $c_{11}$, $c_{12}$, $c_{21}$ y $c_{22}$ se disparan:con flujos entre ellos:y flujos hacia y desde:
ID:(8878, 0)
Simulación básica 600 s
Descripción
Si se considera un sistema que inicialmente no tiene glucosa y que esta en contacto con un lumen con 5.5 mmol/l y con un nervio con 0 mmol/l se tienen los datosque en los primeros 600 s muestran que las concentraciones en los cuatro puntos $c_{11}$, $c_{12}$, $c_{21}$ y $c_{22}$ se disparan:con flujos entre ellos:y flujos hacia y desde:Conclusión:Con los parámetros seteados para la glucosa pasa - inicialmente la membrana es muy lenta pero su superficie mucho mayor que el hatch existiendo flujos similares (62.8% membrana y 37.2% hatch)- en forma asintomática fluye la mayor parte hacia el hatch pasando por este siendo el flujo 99.0% por el hatch y 1.0% por la membrana.Esto significaría que para procesos rápidos la difusión perimetral no juega un papel primordial y la difusión es tanto por la membrana como el hatch. En situaciones lentas sin embargo el hatch juega un papel importante.
ID:(8879, 0)
Modelo de 2 Canales
Modelo
Variables
Cálculos
a 
,
luego, seleccione la variable: 
a 
Cálculos
Variable
Dado
Calcule
Objetivo :
Ecuación
A utilizar
Ecuaciones
Ejemplos
En la medida que la difusi n a lo largo del per metro es menor el sistema se puede modelar con cuatro concentraciones b sicas:
- $c_{11}$ en cavidad entre endotelio y membrana laminar
- $c_{12}$ en primera cavidad frente al hatch
- $c_{21}$ en cavidad entre membrana laminar y membrana exterior
- $c_{22}$ en segunda cavidad frente al hatch
Se consideran ademas las dimensiones geom tricas:
- $l_1$ per metro sin el hatch
- $l_2$ ancho del hatch
- $h$ largo del hatch (que es de mayor largo que la membrana)
- $d_1$ ancho primera cavidad
- $d_2$ ancho segunda cavidad
Se incluyen las constantes de difusi n
- $D_0$ a trav s del endotelio
- $D_1$ a trav s de la membrana laminar
- $D_2$ a trav s de la membrana exterior
- $D$ a trav s del medio liquido (perimetral y hatch)
Se asume adem s de que el sistema no llega al limite de saturaci n.
(ID 8855)
(ID 8865)
Si se considera un sistema que inicialmente no tiene glucosa y que esta en contacto con un lumen con 5.5 mmol/l y con un nervio con 0 mmol/l se tienen los datosque en los primeros 0.5 s muestran que las concentraciones en los cuatro puntos $c_{11}$, $c_{12}$, $c_{21}$ y $c_{22}$ se disparan:con flujos entre ellos:y flujos hacia y desde:
(ID 8878)
Si se considera un sistema que inicialmente no tiene glucosa y que esta en contacto con un lumen con 5.5 mmol/l y con un nervio con 0 mmol/l se tienen los datosque en los primeros 600 s muestran que las concentraciones en los cuatro puntos $c_{11}$, $c_{12}$, $c_{21}$ y $c_{22}$ se disparan:con flujos entre ellos:y flujos hacia y desde:Conclusi n:Con los par metros seteados para la glucosa pasa - inicialmente la membrana es muy lenta pero su superficie mucho mayor que el hatch existiendo flujos similares (62.8% membrana y 37.2% hatch)- en forma asintom tica fluye la mayor parte hacia el hatch pasando por este siendo el flujo 99.0% por el hatch y 1.0% por la membrana.Esto significar a que para procesos r pidos la difusi n perimetral no juega un papel primordial y la difusi n es tanto por la membrana como el hatch. En situaciones lentas sin embargo el hatch juega un papel importante.
(ID 8879)
ID:(1088, 0)