Boyle-Mariotte Law
Storyboard 
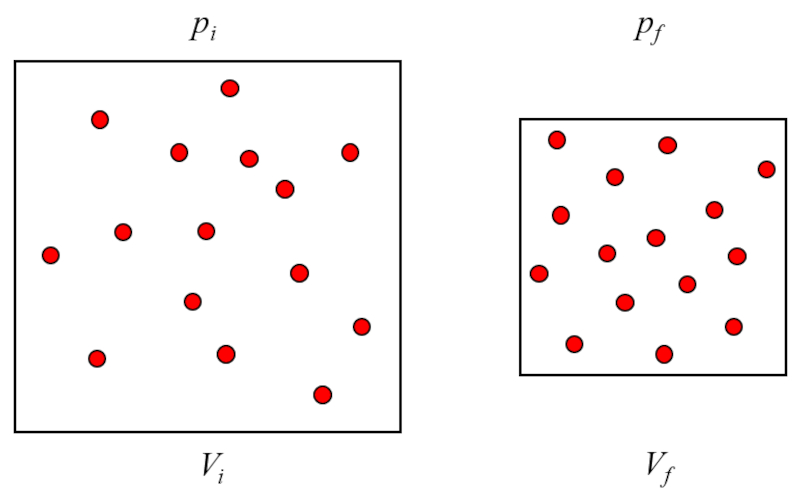
Boyle's Law states that the product of the pressure ($p$) and the volume ($V$) of a gas remains constant when the absolute temperature and the amount of substance do not vary.
This means that the pressure ($p$) varies inversely proportional to the volume ($V$).
ID:(1472, 0)
Boyle-Mariotte Law
Storyboard 
Boyle's Law states that the product of 5224 and 5226 of a gas remains constant when the absolute temperature and the amount of substance do not vary. This means that 5224 varies inversely proportional to 5226.
Variables
Calculations
Calculations
Equations
Boyle's law states that with the absolute temperature ($T$) constant, the product of the pressure ($p$) and the volume ($V$) is equal to the boyle's law constant ($C_b$):
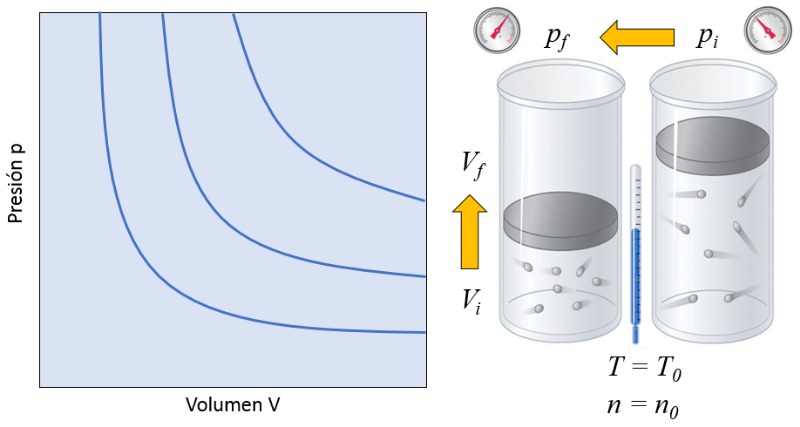
This means that if a gas transitions from an initial state (the pressure in initial state ($p_i$) and the volume in state i ($V_i$)) to a final state (the pressure in final state ($p_f$) and the volume in state f ($V_f$)), maintaining the absolute temperature ($T$) constant, it must always satisfy Boyle's law:
$p_i V_i = C_b = p_f V_f$
Therefore, it follows that:
If in an isothermal change where the content does not vary, the pressure in initial state ($p_i$), the pressure in final state ($p_f$), the volume in state i ($V_i$), and the volume in state f ($V_f$) are related by:
Then, we can introduce the density ($\rho$), which, along with the mass ($M$) and the volume ($V$), satisfies:
This leads us to the density in state i ($\rho_i$) and the density in state f ($\rho_f$) as:
Examples
The Boyle-Mariotte law, also known simply as Boyle's law, describes the inverse relationship between the pressure and volume of a gas at constant temperature. It states that for a fixed amount of gas, when the temperature is held constant, the pressure of the gas increases as the volume decreases, and vice versa. This means that if you compress a gas by reducing its volume, its pressure will increase proportionally, and if you expand the volume, the pressure will decrease proportionally. This relationship is fundamental in understanding gas behavior and is expressed mathematically by the product of pressure and volume being a constant for a given amount of gas at a constant temperature.
The pressure ($p$) is generated when gas particles collide with the surface of the gas container. Since the absolute temperature ($T$) is constant, the energy of the particles does not vary, and the collisions of these particles with the surfaces of the gas container will not vary in the transferred impulse. However, the number of impacts depends on the number of particles near the surface, which in turn is proportional to the the particle concentration ($c_n$) of the gas.
On the other hand, density is inversely proportional to the volume ($V$), leading to the following relationship:
$p \propto c_n \propto \displaystyle\frac{1}{V}$
In a gas, if both the absolute temperature ($T$) and the number of particles ($N$) are kept constant, it is observed that the volume ($V$) and the pressure ($p$) vary inversely. Whenever the volume ($V$) is reduced, the pressure ($p$) increases, and vice versa,
$p \propto \displaystyle\frac{1}{V}$
as illustrated in the following graph:
The relationship between the number of particles ($N$) and the absolute temperature ($T$) is that their product is equal to a boyle's law constant ($C_b$), which corresponds to Boyle's law [1], named after its discoverer Robert Boyle:
Sometimes we talk about the Boyle-Mariotte law, remembering the French physicist Edme Mariotte who discovered the same law independently in 1676.
![]() [1] "New Experiments Physico-Mechanical, Touching the Spring of the Air, and Its Effects," Robert Boyle, Oxford: printed by H. Hall, Printer to the University, for Tho. Robinson (1660).
[1] "New Experiments Physico-Mechanical, Touching the Spring of the Air, and Its Effects," Robert Boyle, Oxford: printed by H. Hall, Printer to the University, for Tho. Robinson (1660).
Robert Boyle was an Irish scientist born in 1627. He is considered one of the founders of modern chemistry and is known for his contributions to the field of gas behavior. Boyle's most significant contribution is his statement of the Boyle's Law, which describes the relationship between the pressure and volume of a gas at constant temperature. Boyle conducted experiments in the mid-17th century that demonstrated that the pressure and volume of a gas are inversely proportional to each other. This relationship became known as Boyle's Law and laid the foundation for the understanding of gas behavior.
Boyle's law states that with the absolute temperature ($T$) constant, the product of the pressure ($p$) and the volume ($V$) is equal to the boyle's law constant ($C_b$):
This means that if a gas transitions from an initial state (the pressure in initial state ($p_i$) and the volume in state i ($V_i$)) to a final state (the pressure in final state ($p_f$) and the volume in state f ($V_f$)), maintaining the absolute temperature ($T$) constant, it must always satisfy Boyle's law:
$p_i V_i = C_b = p_f V_f$
Therefore, it follows that:
If in an isothermal change where the content does not vary, the pressure in initial state ($p_i$), the pressure in final state ($p_f$), the volume in state i ($V_i$), and the volume in state f ($V_f$) are related by:
Then, we can introduce the density ($\rho$), which, along with the mass ($M$) and the volume ($V$), satisfies:
This leads us to the density in state i ($\rho_i$) and the density in state f ($\rho_f$) as:
Boyle's law establishes a relationship between the volume ($V$) and the pressure ($p$), stating that their product is equal to the boyle's law constant ($C_b$) in the following manner:
Boyle's law establishes a relationship between the volume ($V$) and the pressure ($p$), stating that their product is equal to the boyle's law constant ($C_b$) in the following manner:
If a gas transitions from an initial state (i) to a final state (f) with the absolute temperature ($T$) constant, the following relationship holds for the pressure in initial state ($p_i$), the pressure in final state ($p_f$), the volume in state i ($V_i$), and the volume in state f ($V_f$):
Boyle's law for the initial state (the density in state i ($\rho_i$), the pressure in initial state ($p_i$)) and the final state (the density in state f ($\rho_f$), the pressure in final state ($p_f$)) is given by:
ID:(1472, 0)