Osmotic pressure
Storyboard 
Osmotic pressure is generated in a solution when a semipermeable membrane is present. This membrane allows the solvent to pass through while retaining the solute on one side, creating a pressure imbalance. As a result, there is a reduction in pressure on the solvent side, driving the solvent to move through the membrane toward the side containing the solute.
This process continues until the pressure on the solute side increases enough to balance the initial pressure reduction or until the solute becomes diluted enough that the pressure difference is eliminated, reaching osmotic equilibrium.
ID:(660, 0)
Gas phase, water vapor
Definition 
The gaseous phase, which in our case corresponds to water vapor, is the phase in which atoms can move relatively freely.

In this phase, there is only minimal interaction that can affect the behavior of atoms without significantly confining them.
ID:(15142, 0)
Liquid phase, water
Image 
The liquid phase, which in our case corresponds to water, is the phase in which atoms can move relatively freely while maintaining their unity and adapting to the shape that contains them.

In this phase, no specific structure is observed.
ID:(15140, 0)
Phase diagram of water
Exercise 
One of the most relevant phase diagrams for our planet is that of water. This diagram exhibits the three classical phases: solid, liquid, and gas, along with several phases featuring different crystalline structures of ice.
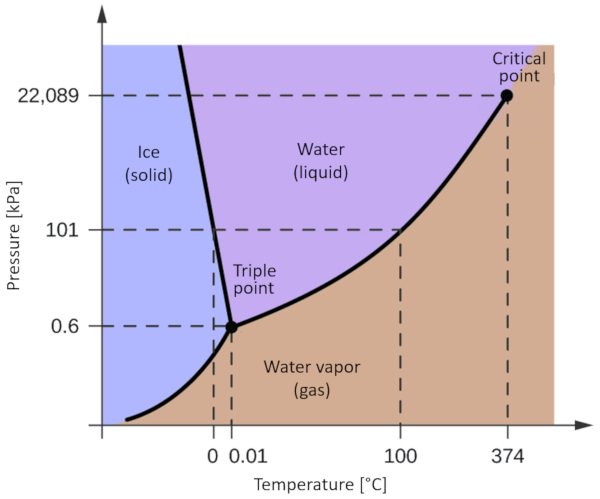
The significant distinction compared to other materials is that within a pressure range spanning from 611 Pa to 209.9 MPa, the solid phase occupies a greater volume than the liquid phase. This characteristic is reflected in the phase diagram as a negative slope along the boundary line separating the solid phase (hexagonal ice) and the liquid phase (water).
ID:(836, 0)
Solid phase, ice
Equation 
The solid phase, which in our case corresponds to ice, is the phase in which atoms cannot move relatively and can only oscillate around their equilibrium point.

In this phase, one can observe a structure that is often crystalline and, therefore, regular.
ID:(15141, 0)
Osmotic pressure
Storyboard 
Osmotic pressure is generated in a solution when a semipermeable membrane is present. This membrane allows the solvent to pass through while retaining the solute on one side, creating a pressure imbalance. As a result, there is a reduction in pressure on the solvent side, driving the solvent to move through the membrane toward the side containing the solute. This process continues until the pressure on the solute side increases enough to balance the initial pressure reduction or until the solute becomes diluted enough that the pressure difference is eliminated, reaching osmotic equilibrium.
Variables
Calculations
Calculations
Equations
If there is the pressure difference ($\Delta p$) between two points, as determined by the equation:
we can utilize the water column pressure ($p$), which is defined as:
This results in:
$\Delta p=p_2-p_1=p_0+\rho_wh_2g-p_0-\rho_wh_1g=\rho_w(h_2-h_1)g$
As the height difference ($\Delta h$) is:
the pressure difference ($\Delta p$) can be expressed as:
The number of moles ($n$) corresponds to the number of particles ($N$) divided by the avogadro's number ($N_A$):
If we multiply both the numerator and the denominator by the particle mass ($m$), we obtain:
$n=\displaystyle\frac{N}{N_A}=\displaystyle\frac{Nm}{N_Am}=\displaystyle\frac{M}{M_m}$
So it is:
Como la energ a molar libre de Gibbs es
se tiene que para el equilibrio entre un sistema con y sin material disuelto (
$\displaystyle\frac{V}{N_A}dp=\displaystyle\frac{V}{N_A}(p - \Phi)=\mu dN=\mu (N-N_s)$
Como sin material disuelto se debe asumir que el vapor satisface la ecuaci n de los gases se tiene que
$\mu\sim \displaystyle\frac{R}{N_A} T$
con lo que se obtiene que
Examples
When a semipermeable membrane is placed at the bottom of a U-shaped tube and water is added, it can be observed that adding dissolved material causes the column with the solute to rise:
This phenomenon is due to the negative pressure generated by osmotic pressure.
The osmotic pressure ($\Psi$) behaves like the pressure of an ideal gas of the number of ions ($N_s$) in the volume ($V$) at the absolute temperature ($T$), using the universal gas constant ($R_C$) as described by:
If two columns of water are separated at their base by a semipermeable membrane that allows water to pass through but blocks the solute present in one of them, the columns will exhibit different heights. This is because the presence of a solute reduces the osmotic pressure, leading to an adjustment in the height of the column to balance the pressure difference.
If the pressure in the first column is the pressure in column 1 ($p_1$), the pressure in the second column (without solute) is the pressure in column 2 ($p_2$), and the osmotic pressure is the osmotic pressure ($\Psi$), we can express the relationship as follows:
The height difference, denoted by the height difference ($\Delta h$), implies that the pressure in both columns is distinct. In particular, the pressure difference ($\Delta p$) is a function of the liquid density ($\rho_w$), the gravitational Acceleration ($g$), and the height difference ($\Delta h$), as follows:
When two liquid columns are connected with the height of liquid column 1 ($h_1$) and the height of liquid column 2 ($h_2$), a the height difference ($\Delta h$) is formed, which is calculated as follows:
the height difference ($\Delta h$) will generate the pressure difference that will cause the liquid to flow from the higher column to the lower one.
When two liquid columns are connected with the pressure in column 1 ($p_1$) and the pressure in column 2 ($p_2$), a the pressure difference ($\Delta p$) is formed, which is calculated according to the following formula:
the pressure difference ($\Delta p$) represents the pressure difference that will cause the liquid to flow from the taller column to the shorter one.
The number of moles ($n$) corresponds to the number of particles ($N$) divided by the avogadro's number ($N_A$):
the avogadro's number ($N_A$) is a universal constant with a value of 6.028E+23 1/mol, and is therefore not included among the variables used in the calculation.
The number of moles ($n$) is determined by dividing the mass ($M$) of a substance by its the molar Mass ($M_m$), which corresponds to the weight of one mole of the substance.
Therefore, the following relationship can be established:
The molar mass is expressed in grams per mole (g/mol).
The water column pressure ($p$) is with the liquid density ($\rho_w$), the column height ($h$), the gravitational Acceleration ($g$) and the atmospheric pressure ($p_0$) equal to:
The water column pressure ($p$) is with the liquid density ($\rho_w$), the column height ($h$), the gravitational Acceleration ($g$) and the atmospheric pressure ($p_0$) equal to:
ID:(660, 0)
