Ocupación de estados
Definición 
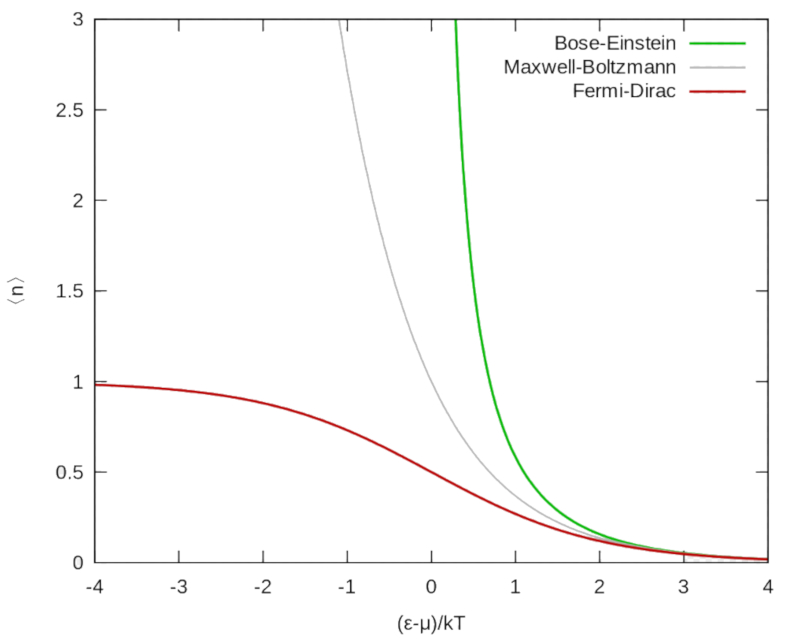
Si se compara la ocupación de estados se obtiene que
- la distribución de Fermi-Direc (FD) disminuye con la energía por temperatura
- la distribución de Bose Einstein (BE) aumenta con la energía por temperatura
- la distribución de Maxwell-Boltzmann (MB) muestra un comportamiento intermedio
- ambas distribuciones de los gases cuanticos (FD, BE) convergen a alta energía por temperatura a la distribución de Maxwell Boltzmann
ID:(13508, 0)
Potencial químico en las tres distribuciones
Imagen 
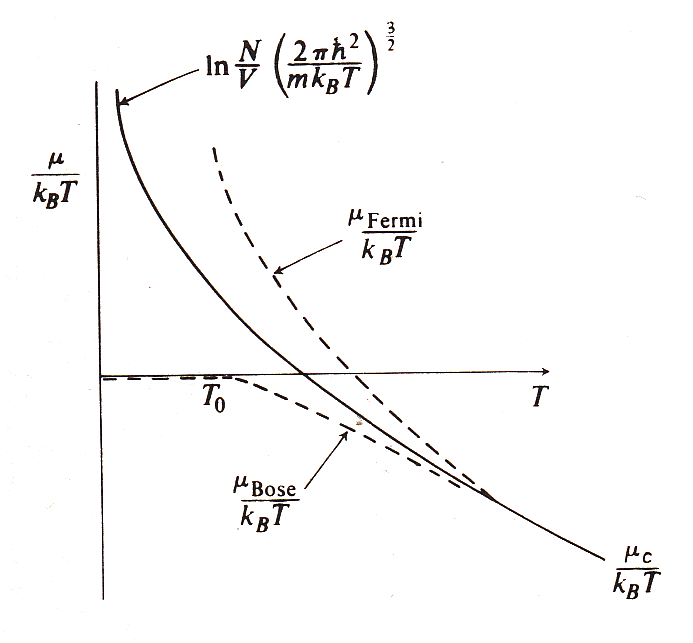
En el caso del potencial químico se observa
- en la distribución de Fermi-Direc (FD) que decrece al aumentar la temperatura volviéndose negativo
- en la distribución de Bose Einstein (BE) que presenta el condensado (en que es cero) y de igual forma decrece con el aumento de la temperatura
- en la distribución de Maxwell-Boltzmann (MB) muestra un comportamiento intermedio
- ambas distribuciones de los gases cuanticos (FD, BE) convergen a alta energía por temperatura altas a la distribución de Maxwell Boltzmann
ID:(13509, 0)
Límites de Estadísticas de Gases Cuánticos
Descripción 
Variables
Cálculos
Cálculos
Ecuaciones
Ejemplos
En el caso de la distribuci n Maxwell Boltzmann la funci n partici n cl sica es\\n\\n
$Z_{MB}=\displaystyle\sum_{n_1,n_2,\ldots}\displaystyle\frac{N!}{n_1!n_2!\ldots}e^{-\beta(\epsilon_1+\epsilon_2+\ldots}$
con la condici n de que con
| $ N =\displaystyle\sum_ r n_r $ |
\\n\\nSi observamos la funci n partici n notaremos que corresponde a una serie binomial por lo que\\n\\n
$Z_{MB}=(e^{-\beta\epsilon_1}+e^{-\beta\epsilon_2}+\ldots)^N$
por lo que con
| $ \ln Z_{MB} = N \ln\left(\displaystyle\sum_ r e^{- \beta \epsilon_r }\right)$ |
(ID 3736)
El n mero de part culas en el estado
| $ n_r =\displaystyle\frac{1}{e^{ \alpha + \beta \epsilon_r }-1}$ |
y en el caso de fermiones con mediante
| $ n_r =\displaystyle\frac{1}{e^{ \alpha + \beta \epsilon_r }+1}$ |
o sea en general con
| $n_r=\displaystyle\frac{1}{e^{\alpha+\beta\epsilon_r}\pm 1}$ |
(ID 3732)
En el caso bajas concentraciones en
$n_r\ll 1$
\\n\\ny por ello\\n\\n
$e^{\alpha+\beta\epsilon_r}\gg 1$
en
| $n_r=\displaystyle\frac{1}{e^{\alpha+\beta\epsilon_r}\pm 1}$ |
nos da con caso
| $n_r=e^{-\alpha-\beta\epsilon_r}$ |
(ID 3734)
Si se compara la ocupaci n de estados se obtiene que
- la distribuci n de Fermi-Direc (FD) disminuye con la energ a por temperatura
- la distribuci n de Bose Einstein (BE) aumenta con la energ a por temperatura
- la distribuci n de Maxwell-Boltzmann (MB) muestra un comportamiento intermedio
- ambas distribuciones de los gases cuanticos (FD, BE) convergen a alta energ a por temperatura a la distribuci n de Maxwell Boltzmann

(ID 13508)
Tanto para bosones como para fermiones el factor alfa debe ser elegido de modo que la suma del numero de part culas sobre todos los estados sea igual al numero total de part culas por lo que con se tiene que
| $ N =\displaystyle\sum_ r \displaystyle\frac{1}{e^{ \alpha + \beta \epsilon_r }\pm 1}$ |
(ID 3731)
Como el n mero de part culas por estado
| $n_r=e^{-\alpha-\beta\epsilon_r}$ |
y la suma sobre todos los estados debe ser igual al n mero total
| $ N =\displaystyle\sum_ r n_r $ |
se obtiene que
| $ \alpha =- \ln N +\ln\left(\displaystyle\sum_ r e^{- \beta \epsilon_r }\right)$ |
(ID 3735)
La funci n partici n para un gas de bosones es con igual a
| $ \ln Z_{BE} = \alpha N -\displaystyle\sum_ r \ln(1-e^{- \beta \epsilon_r - \alpha })$ |
mientras que la del gas de fermiones es con igual a
| $ \ln Z_{FD} = \alpha N +\displaystyle\sum_ r \ln(1+e^{- \alpha - \beta \epsilon_r })$ |
por lo que en general con tiene la forma
| $ \ln Z_{BE/FD} = \alpha N \pm\displaystyle\sum_ r \ln(1\pm e^{- \alpha - \beta \epsilon_r })$ |
(ID 3733)
Con las funciones de particion del gas de bosones y fermiones en el limite cl sico es con alpha $-$, beta $1/J$, energía de la partícula en el estado $r$ $J$, función partición de Bose-Einstein/Fermi-Dirac $-$ y numero de partículas $-$
| $ \ln Z_{BE/FD} = \alpha N \pm\displaystyle\sum_ r \ln(1\pm e^{- \alpha - \beta \epsilon_r })$ |
que con alpha $-$, beta $1/J$, energía de la partícula en el estado $r$ $J$ y numero de partículas en el estado $r$ $-$
| $n_r=e^{-\alpha-\beta\epsilon_r}$ |
\\n\\nen la aproximaci n cl sica es\\n\\n
$n_r\ll 1,,e^{-\alpha-\beta\epsilon_r}\ll 1$
\\n\\nCon ello se puede desarrollar el logaritmo en serie de Taylor dando\\n \\n
$\ln Z_{BE/FD}\displaystyle\sim\alpha N\pm\displaystyle\sum_r(\pm e^{-\alpha-\beta\epsilon})=\alpha N+N$
Con la expresi n para
| $ \alpha =- \ln N +\ln\left(\displaystyle\sum_ r e^{- \beta \epsilon_r }\right)$ |
se obtiene con beta $1/J$, energía de la partícula en el estado $r$ $J$, función partición de Maxwell-Boltzmann $-$ y numero de partículas $-$
| $ \ln Z_{MB} = N \ln\left(\displaystyle\sum_ r e^{- \beta \epsilon_r }\right)$ |
\\n\\nque\\n\\n
$\ln Z_{BE/FD}=-N\ln N+N+\ln Z_{MB}$
Como con
| $\ln N!\sim N\ln N-N$ |
se obtiene finalmente que con es
| $ Z_{BE/FD} =\displaystyle\frac{1}{ N !} Z_{MB} $ |
(ID 3737)
En el caso del potencial qu mico se observa
- en la distribuci n de Fermi-Direc (FD) que decrece al aumentar la temperatura volvi ndose negativo
- en la distribuci n de Bose Einstein (BE) que presenta el condensado (en que es cero) y de igual forma decrece con el aumento de la temperatura
- en la distribuci n de Maxwell-Boltzmann (MB) muestra un comportamiento intermedio
- ambas distribuciones de los gases cuanticos (FD, BE) convergen a alta energ a por temperatura altas a la distribuci n de Maxwell Boltzmann

(ID 13509)
ID:(514, 0)
