Storyboard

Every area of physics is characterized by a key concept and one or more associated equations. In mechanics, it revolves around describing motion, with Newton's laws as the key equations. In electromagnetism, the focus is on understanding the interaction of electric charges, where the primary equation is Coulomb's law, which dictates that the force decreases quadratically with distance. Similarly, in quantum mechanics, we have Schrödinger's equation and the concept of the wave function.

In statistical mechanics, the challenge lies in modeling systems composed of multiple particles, which may initially appear impossible to solve. However, with a rather straightforward idea, the problem is reduced to counting states based on microscopic parameters and calculating the probabilities associated with macroscopic states. Microscopic states are described in terms of the phase space unique to mechanics, and they are quantified to determine the probability distribution, allowing us to statistically analyze the likelihood of the system exhibiting a specific behavior.

>Model

ID:(307, 0)

Description

>Top

In mechanics we learn that we can model how bodies behave. However, if we consider a system as a gas we will have 10^{23} particles, the application of the concepts of mechanics becomes complicated. On the one hand there is the high complexity of solving a system of 10^{23} equations, on the other hand we would not know what to do with this result. Therefore, we must seek another approach.

One possibility would be not to work with individual solutions but rather with their distributions. That is, not to calculate the behavior of each particle but rather to develop a theory that, based on concepts of quantum mechanics or mechanics, allows us to calculate the distribution that tells us how the solutions are distributed.

The question now is how can we calculate these distributions?

ID:(502, 0)

Description

>Top

Video 'What is NOT Random' by Derek Muller

It is not about Statistical Mechanics but it helps to understand many related concepts that are discussed (with images from the video) in the next few slides.

ID:(13040, 0)

Image

>Top

Laplace introduces the concept of an observer (later caricatured as Laplace's demon) who observes all the positions of all the particles in a system and all the interactions that exist and can with it:
- forecast future developments
- determine past history

With this the world becomes deterministic. There is no chance. Nor would free will exist:

- every decision that we apparently make is the deterministic consequence of the situation in which we found ourselves

- in that sense we would not be responsible for our actions since there is no possibility that we can freely choose

ID:(13041, 0)

Image

>Top

Physics is therefore the rules that allow me to calculate the new state from a previous state.
As an analogy, if one considers a video it can be broken down into multiple pixels. From one frame to the other only a few pixels change.

The rules of behavior therefore indicate

- which pixels change

- in what way do they change

ID:(13042, 0)

Image

>Top

The key question is whether a system in a simple state (little information) evolves in such a way that the information is preserved. This is, complex as it may seem, it does not increase the amount of information it contains.

As the equations of motion are invariant under a reversal of time, this would mean that the system can return to its initial state spontaneously. It would seem that it is 'ordered' because it never really 'messed up'.

However, we know that this is not the case:

Systems do not return spontaneously to their initial 'ordered' state, so there is a natural 'disordering'.

Disordering means that more information is required to describe the system. Thus

Information is not preserved over time and tends to increase.

The amount of information in a system is called its entropy.

ID:(13043, 0)

Image

>Top

The increase in information leads to:
- there are more than one new state that the system can assume, not existing the possibility of predicting which state the system assumes
- it may be possible to determine the system that originates the final state

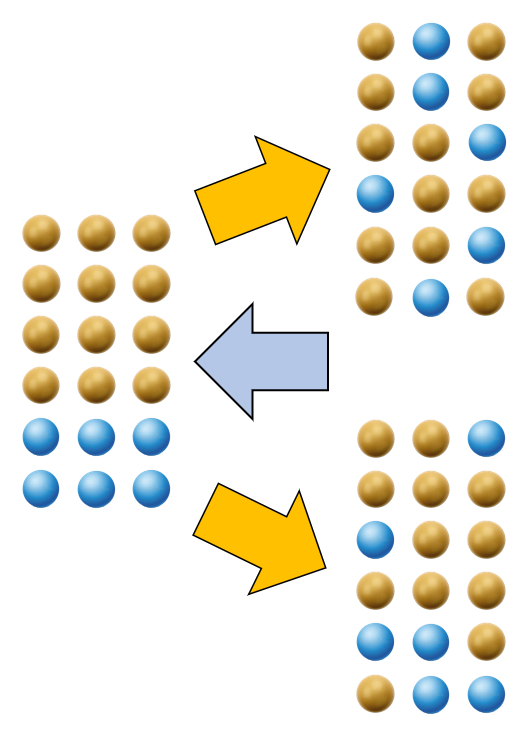
This leads to

- you can only give a probability of a new state that the system will assume

- in an analogous way, the return to the original system is associated with a probability and this can be infinitesimal

ID:(13046, 0)

Image

>Top

Long before quantum mechanics was discovered within thermodynamics, the so-called Gibbs paradox arose. This arises when one tries to add the entropy of two individual systems and compares it with that of a system the size of both combined.

The solution of the paradox leads to the determination that the particles of which the system is made up have to be indistinguishable. This leads to the fact that when they interact it is not possible to know which one corresponds to which implying that new alternatives are created:

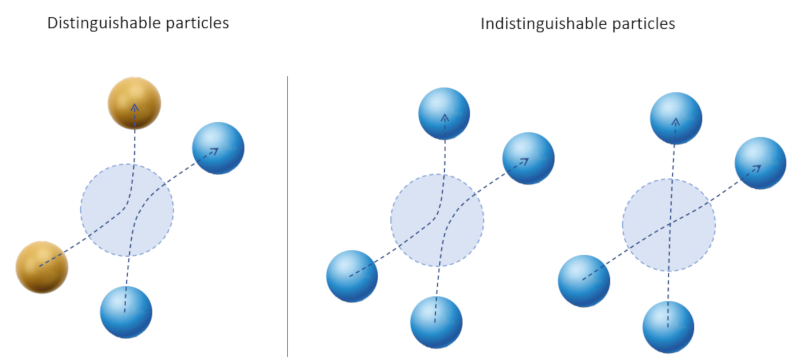
The new alternatives correspond to additional information that must be had to define the possible states.

Note: Derek Muller video of Veritasium's explores the quantum mechanical effect without alluding to the Gibbs paradox.

ID:(13044, 0)

Image

>Top

Statistical mechanics does not seek to solve the equations of motion of the system. It seeks to recognize how the equations of motion limit the possible states, recognizing general patterns that allow describing the state of the system and its evolution.

In the analogy of an image, the situation of maximum information (entropy) and in turn of perfect chaos is a frame of pixels chosen at random.

A real system presents a structure, an order, which in the analogy of the painting would correspond to an image in which structures such as the grouping of colors are recognized. Variations within said pixels will not be recognized, being an equivalent frame for the observer. The analogous occurs in a physical system in which there are multiple variations on the conditions that describe the same macro-state of the system. In that sense

statistical mechanics studies assemblies (sets) of possible states based on macroscopic parameters that limit them and determines their probability of their existence.

ID:(13045, 0)

Description

>Top

The multiple alternatives that mean 10^{23} particles are on a microscopic level.

Yet many of those microscopic states are very similar if not identical on a macroscopic level.

If in the end there is only a discrete number of possible macroscopic states, its probability of existence can be estimated as a function of the number of microscopic states that are associated with them.

In this way statistical mechanics solves the problem

• determining the possible microscopic states

• determining the macroscopic states that are associated with the microscopic ones

• determining through the number of microscopic states the probability of each macroscopic state

ID:(11400, 0)

Description

>Top

When seeking to describe the state of the system of 10^{23} particles we resort to mechanics establishing the equations the equations that define the possible physical states of the system.

For it:

possible states in the phase system p-q are considered

The restrictions that exist on the possible states are studied (example given total energy)

methods are sought to be able to count the number of states that exist under the given restrictions

ID:(11401, 0)

Description

>Top

When obtaining the possible macroscopic states and the frequency it is necessary to develop a work of statistical analysis :.

• establish the probability distribution of each macroscopic state

• study how the distribution evolves as a function of the macroscopic parameters of the system

• in most cases the result is that there is a high probability macroscopic state and

• the distribution provides information about the dispersion that the different parameters may have

ID:(11402, 0)

0

Video

Video: What is Statistical Mechanics?