Storyboard

>Model

ID:(557, 0)

Equation

>Top, >Model

Cuando se definió la entropía al principio la asociamos con el numero de combinaciones posibles \Omega con mediante

\\n\\ndonde k era la constante de Boltzmann. Si empleamos el modelo del tablero de ajedrez veremos que la cantidad de formas en que podemos combinar las partículas N_s en los casilleros del tablero se calculan con combinatórica dando\\n\\n

$\Omega=\displaystyle\frac{(N+N_s)!}{N!N_s!}$

\\n\\nPor ello la variación de la entropía por la distribución del soluto es igual a\\n\\n

$\Delta S=k\ln\left(\displaystyle\frac{(N+N_s)!}{N!N_s!}\right)$

\\n\\nComo el logaritmo de un factorial se puede aproximar por\\n\\n

$\ln N!=N\ln N-N$

la variación de la entropía se puede expresar con como

ID:(4150, 0)

Equation

>Top, >Model

En el caso de una solución débil\\n\\n

$N_s\ll N$

se puede expandir el cambio de entropía con constante de Boltzmann $J/K$, numero de partículas de soluto $-$, numero de partículas del solvente $-$ and variación de la entropía por mezcla $J/K$

\\n\\nen torno a N_s/N\ll 1 lo que nos da con\\n\\n

$\ln\displaystyle\frac{1}{1+x}\sim -x+\displaystyle\frac{1}{2}x^2\ldots$

\\n\\ny\\n\\n

$\ln\displaystyle\frac{x}{1+x}\sim \ln x-x+\displaystyle\frac{1}{2}x^2\ldots$

que \Delta S es con constante de Boltzmann $J/K$, numero de partículas de soluto $-$, numero de partículas del solvente $-$ and variación de la entropía por mezcla $J/K$

ID:(4151, 0)

Equation

>Top, >Model

Como la función de Gibbs es igual con a

$G(T,p,N,N_s)= N g_0(T,p) + \Psi V - T \Delta S $

en donde g_0 es la energía libre de Gibbs molar del solvente, \Psi la presión de las partículas del soluto y \Delta S la variación de la entropía por efecto de la mezcla.

Como la variación de la entropía es con constante de Boltzmann $J/K$, numero de partículas de soluto $-$, numero de partículas del solvente $-$ and variación de la entropía por mezcla $J/K$

se tiene que la energía libre de Gibbs de la mezcla es con constante de Boltzmann $J/K$, numero de partículas de soluto $-$, numero de partículas del solvente $-$ and variación de la entropía por mezcla $J/K$

ID:(4152, 0)

Equation

>Top, >Model

Para obtener el potencial químico del solvente basta derivar la función de Gibbs con constante de Boltzmann $J/K$, energía libre de Gibbs de la solución $J$, energía libre de Gibbs del solvente por partícula $J$, numero de partículas de soluto $-$, numero de partículas del solvente $-$, presión de las partículas del soluto $Pa$ and temperature $K$

respecto del número de partículas del solvente N con

De esta forma se obtiene con

ID:(4153, 0)

Image

>Top

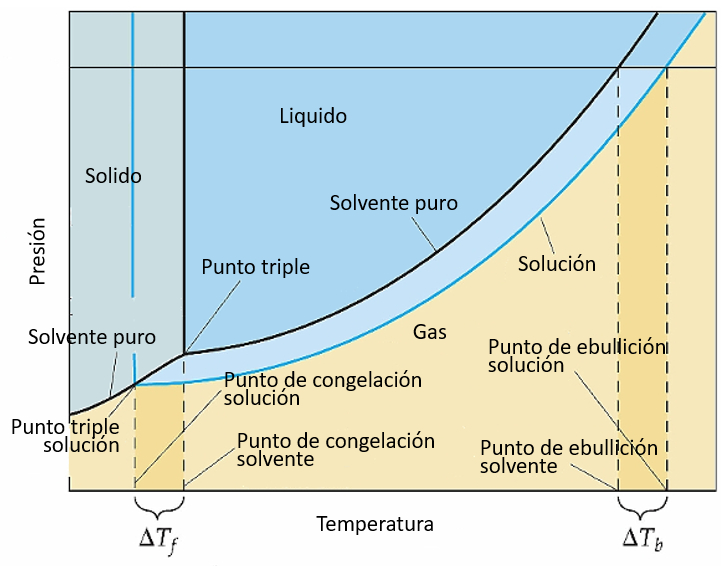
In a phase diagram of a solution, the boundaries between phases shift in such a way that, at the same pressure, the melting point decreases while the boiling point increases:

ID:(1980, 0)

Equation

>Top, >Model

El potencial químico de una solución es igual con constante de Boltzmann $J/K$, energía libre de Gibbs del solvente por partícula $J$, numero de partículas de soluto $-$, numero de partículas del solvente $-$, potencial químico del solvente $J$ and temperature $K$ a

\\n\\nque se puede expandir en torno a una temperatura en particular T_0, que puede ser por ejemplo la temperatura de ebullición o congelación, dando\\n\\n

$\mu_L^0(T,p)=\mu_L(T_0,p)+\left(\displaystyle\frac{\partial\mu_L}{\partial T}\right)_p(T-T_0)-\displaystyle\frac{N_s}{N}k_BT$

Como con entropía molar $J/mol K$, numero de Avogadro $-$, numero de partículas $-$, potencial químico $J$ and temperature $K$

se tiene finalmente que el potencial químico de una solución es con entropía molar $J/mol K$, numero de Avogadro $-$, numero de partículas $-$, potencial químico $J$ and temperature $K$

ID:(9046, 0)

Equation

>Top, >Model

El potencial químico del solido es igual a una función \mu_S(T,p,N) que se puede expandir en torno a una temperatura en particular T_0, que puede ser por ejemplo la temperatura de ebullición o congelación, dando\\n\\n

$\mu_S^0(T,p)=\mu_S(T_0,p)+\left(\displaystyle\frac{\partial\mu_S}{\partial T}\right)_p(T-T_0)$

Como con entropía molar $J/mol K$, numero de Avogadro $-$, numero de partículas $-$, potencial químico $J$ and temperature $K$ es

se tiene finalmente que el potencial químico de una solución es entropía molar $J/mol K$, numero de Avogadro $-$, numero de partículas $-$, potencial químico $J$ and temperature $K$

ID:(9048, 0)

Equation

>Top, >Model

El potencial químico del vapor es igual a una función \mu_V(T,p,N) que se puede expandir en torno a una temperatura en particular T_0, que puede ser por ejemplo la temperatura de ebullición o congelación, dando\\n\\n

$\mu_V^0(T,p)=\mu_V(T_0,p)+\left(\displaystyle\frac{\partial\mu_V}{\partial T}\right)_p(T-T_0)$

Como con entropía molar $J/mol K$, numero de Avogadro $-$, numero de partículas $-$, potencial químico $J$ and temperature $K$

se tiene finalmente que el potencial químico de una solución es con entropía molar $J/mol K$, numero de Avogadro $-$, numero de partículas $-$, potencial químico $J$ and temperature $K$

ID:(9047, 0)

Equation

>Top, >Model

Como el potencial químico en función de la energía de Gibbs es con

y ademas con

\\n\\nse tiene que\\n\\n

$\left(\displaystyle\frac{\partial\mu}{\partial T}\right)_p=-S$

\\n\\nComo S es extensible, se tiene que se puede escribir en función de su valor molar s\\n\\n

$S(T,p)=\displaystyle\frac{N}{N_A}s(T,p)$

y finalmente con

ID:(9049, 0)

Equation

>Top, >Model

If the temperatura de fusión ($T_f$) represents the boiling temperature, the molar entropy of the liquid ($s_L$) corresponds to the molar entropy of the liquid, and the molar entropy of the solid ($s_S$) to that of the solid, then the enthalpy of evaporation the calor latente molar del cambio de fase solido liquido ($l_S$) is calculated using the following formula:

$ l_S = T_f ( s_L - s_S )$

Conditions

Variables

$l_S$

Calor latente molar del cambio de fase solido liquido

$J/mol$

9497

$s_L$

Molar entropy of the liquid

$J/mol K$

9855

$s_S$

Molar entropy of the solid

$J/mol K$

9856

$T_f$

Temperatura de fusión

$K$

9498

Relation

ID:(9051, 0)

Equation

>Top, >Model

If the boiling temperature ($T_b$) is the boiling temperature, the molar entropy of vapor ($s_V$) represents the molar entropy of the vapor, and the molar entropy of the liquid ($s_L$) represents that of the liquid, then the enthalpy of evaporation the calor latente molar del cambio de fase liquido vapor ($l_V$) is calculated using the following expression:

$ l_V = T_b ( s_V - s_L )$

Conditions

Variables

$T_b$

Boiling temperature

$K$

9861

$l_V$

Calor latente molar del cambio de fase liquido vapor

$J/mol$

9501

$s_L$

Molar entropy of the liquid

$J/mol K$

9855

$s_V$

Molar entropy of vapor

$J/mol K$

9854

Relation

ID:(9050, 0)

Equation

>Top, >Model

Otro efecto que varia en soluciones es el punto de ebullición. Al momento de hervir el solvente a una temperatura T y presión p en su estado puro, el potencial químico de este en forma liquida debe de ser igual a aquel en forma de vapor:\\n\\n

$\mu_L^0(T,p)=\mu_V^0(T,p)$

Si se considera como temperatura de referencia T_0 la del punto de ebullición del liquido T_b, el potencial quimico de la solución es con constante de Boltzmann $J/K$, molar entropy of the liquid $J/mol K$, numero de Avogadro $-$, numero de partículas de soluto $-$, numero de partículas del solvente $-$, potencial químico del liquido $J$, temperatura del sistema $K$ and temperature $K$

y el del vapor molar entropy of vapor $J/mol K$, numero de Avogadro $-$, potencial químico del vapor $J$, temperatura del sistema $K$ and temperature $K$

\\n\\nse tiene que la temperatura de ebullición de la solución T_s estará definida por\\n\\n

$\displaystyle\frac{s_L}{N_A}(T_s-T_b)-\displaystyle\frac{N_s}{N}k_BT_s=\displaystyle\frac{s_V}{N_A}(T_s-T_b)$

Con boiling temperature $K$, calor latente molar del cambio de fase liquido vapor $J/mol$, molar entropy of the liquid $J/mol K$ and molar entropy of vapor $J/mol K$

y con

se tiene que con

ID:(4065, 0)

Equation

>Top, >Model

Otro efecto que varia en soluciones es el punto de congelación. Al momento de congelarse el solvente a una temperatura T y presión p en su estado puro, el potencial químico de este en forma solida debe de ser igual a aquel en forma de liquida:\\n\\n

$\mu_S^0(T,p)=\mu_L^0(T,p)$

Si se considera como temperatura de referencia T_0 la del punto de ebullición del liquido T_b, el potencial químico de la solución es constante de Boltzmann $J/K$, molar entropy of the liquid $J/mol K$, numero de Avogadro $-$, numero de partículas de soluto $-$, numero de partículas del solvente $-$, potencial químico del liquido $J$, temperatura del sistema $K$ and temperature $K$

y el del solido con molar entropy of the solid $J/mol K$, numero de Avogadro $-$, potencial químico del solido $J$, temperatura del sistema $K$ and temperature $K$

\\n\\nse tiene que la temperatura de ebullición de la solución T_s estara definida por\\n\\n

$\displaystyle\frac{s_S}{N_A}(T_s-T_b)=\displaystyle\frac{s_L}{N_A}(T_s-T_b)-\displaystyle\frac{N_s}{N}kT_s$

Con calor latente molar del cambio de fase solido liquido $J/mol$, molar entropy of the liquid $J/mol K$, molar entropy of the solid $J/mol K$ and temperatura de fusión $K$

y con

se tiene que con

ID:(4066, 0)

Description

>Top

ID:(865, 0)

Equation

>Top, >Model

En el caso de una solución binaria ambas componentes pueden figurar en proporciones similares por lo que no es posible realizar la aproximación de soluciones débiles. En este caso la variación de la entropía permanece de la forma\\n\\n

$\Delta S=-k\left(N\ln\displaystyle\frac{N_A}{N_A+N_B}+N_B\ln\displaystyle\frac{N_B}{N_A+N_B}\right)$

donde A y B son las dos componentes. En este caso la función de Gibbs es, incluyendo un factor de interacción escalado en \lambda con ,

ID:(4156, 0)