Storyboard

The light is irradiated, that is to say it flows so that the fundamental magnitudes refer to the amount of photons that are emitted, cross a section or are absorbed.

Since the amount of photons in a color is proportional to the energy, the flow is proportional to the energy per time, that is, the power.

>Model

ID:(297, 0)

Image

>Top

If we think of light as a flow of photons, they will move away from their source and spread over an increasingly larger surface:

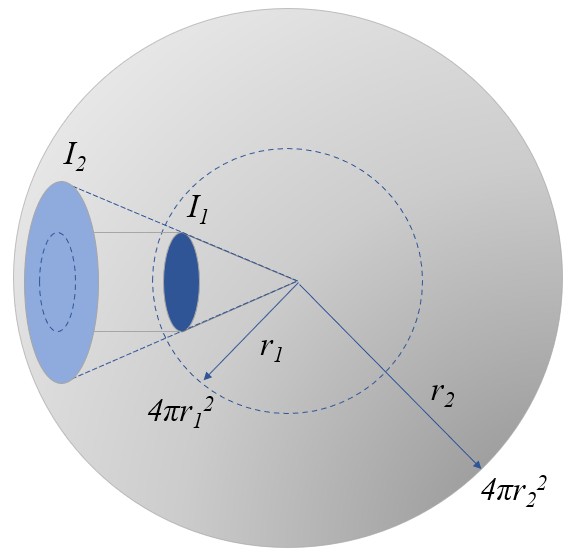
In this way, the intensity decreases as we move away from the source, diminishing inversely with the square of the distance.

ID:(1664, 0)

Description

>Top

When light passes through the aperture, the intensity depends on the angle of the beam relative to the original direction of the beam, denoted as $\theta$.

The intensity $I$ is given by

$I(r,\theta)=\displaystyle\frac{r_0^2}{r^2}I_0\cos\theta$

Conditions

Variables

$\theta$

Angle of Propagation

$rad$

5139

$r$

Distance to Source

$m$

5137

$I$

Light Intensity

$W/m^2$

5140

$L$

luminosity

$Cd$

5138

Relation

ID:(3352, 0)

Image

>Top

When light passes through an aperture, it begins to disperse. Its intensity decreases both with the distance from the aperture and with the angle relative to the original direction of propagation:

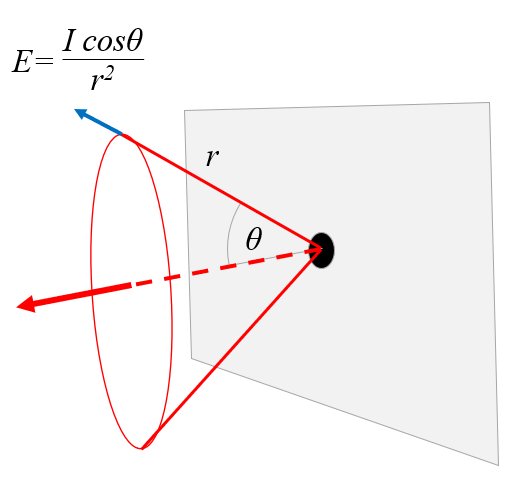
ID:(1861, 0)

Equation

>Top, >Model

Since photons are distributed over an area of size $4\pi r^2$, the number per unit area of these photons decreases. As the number of photons per unit area is the density, it reduces as follows:

$I_r =\displaystyle\frac{ r_0 ^2}{ r ^2} I_0$

Conditions

Variables

$r_1$

Distancia a la fuente 1

$m$

9829

$r_2$

Distancia a la fuente 2

$m$

9830

$I_1$

Intensidad de la luz 1

$W/m^2$

9831

$I_2$

Intensidad de la luz 2

$W/m^2$

9832

Relation

Intensity is measured in candelas (cd), which is the amount of light emitted by an object at a temperature of $2042.5 K$ over an area of size $1/600000 m^2$.

ID:(3191, 0)