Storyboard

Das Licht wird eingestrahlt, dh es fließt so, dass sich die Grundgrößen auf die Menge der Photonen beziehen, die emittiert werden, einen Querschnitt durchqueren oder absorbiert werden.

Da die Menge der Photonen in einer Farbe proportional zur Energie ist, ist der Fluss proportional zur Energie pro Zeit, dh der Leistung.

>Modell

ID:(297, 0)

Bild

>Top

Wenn wir Licht als einen Fluss von Photonen betrachten, entfernen sich diese von ihrer Quelle und verteilen sich über eine immer größere Fläche:

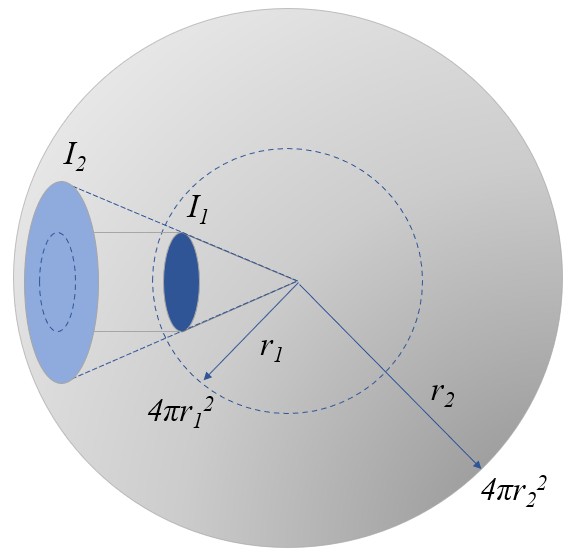
Auf diese Weise nimmt die Intensität ab, wenn wir uns von der Quelle entfernen, und zwar umgekehrt proportional zum Quadrat der Entfernung.

ID:(1664, 0)

Beschreibung

>Top

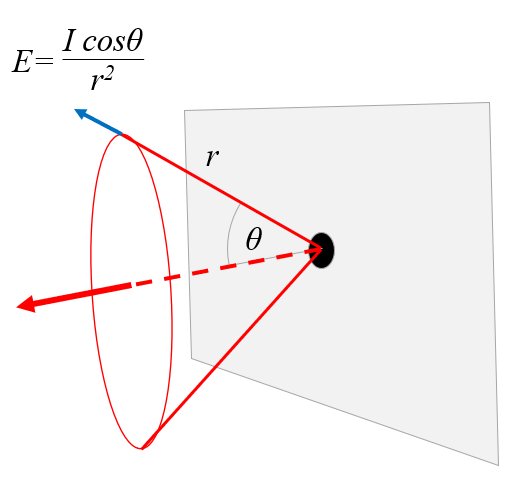
Wenn Licht durch die Öffnung hindurchtritt, hängt die Intensität vom Winkel des Strahls in Bezug auf die ursprüngliche Richtung des Strahls ab, dargestellt als $\theta$.

Die Intensität $I$ wird durch folgenden Ausdruck beschrieben:

$I(r,\theta)=\displaystyle\frac{r_0^2}{r^2}I_0\cos\theta$

Bedingungen

Variablen

$\theta$

Ausbreitungswinkel

$rad$

5139

$r$

Entfernung zur Quelle

$m$

5137

$I$

Lichtintensität

$W/m^2$

5140

$L$

Lichtstärke

$Cd$

5138

Beziehung

ID:(3352, 0)

Bild

>Top

Wenn Licht durch eine Öffnung tritt, beginnt es sich zu verteilen. Die Intensität nimmt sowohl mit dem Abstand von der Öffnung als auch mit dem Winkel relativ zur ursprünglichen Ausbreitungsrichtung ab:

ID:(1861, 0)

Gleichung

>Top, >Modell

Da Photonen sich über eine Fläche der Größe $4\pi r^2$ verteilen, nimmt die Anzahl pro Flächeneinheit dieser Photonen ab. Da die Anzahl der Photonen pro Flächeneinheit die Dichte darstellt, reduziert sie sich wie folgt:

$I_r =\displaystyle\frac{ r_0 ^2}{ r ^2} I_0$

Bedingungen

Variablen

$r_1$

Distancia a la fuente 1

$m$

9829

$r_2$

Distancia a la fuente 2

$m$

9830

$I_1$

Intensidad de la luz 1

$W/m^2$

9831

$I_2$

Intensidad de la luz 2

$W/m^2$

9832

Beziehung

Die Intensität wird in Candela (cd) gemessen, was der Menge an Licht entspricht, die von einem Objekt bei einer Temperatur von $2042,5 K$ über eine Fläche von $1/600000 m^2$ abgestrahlt wird.

ID:(3191, 0)