Generación de Torque
Storyboard 
El torque se genera mediante una fuerza aplicada a una cierta distancia del eje de rotación. Fuerzas sobre un punto en el eje de rotación solo llevan a traslación y no inducen cambios en la rotación o torque.La distancia mas corta entre el punto que ataca la fuerza y el eje se denomina brazo y este es siempre perpendicular al eje. Una fuerza paralela al brazo solo genera traslación del eje por lo que solo las fuerzas perpendiculares al brazo son las que generan torque.Finalmente se ve que el torque es mayor mientras mayor es el brazo y mayor es la fuerza perpendicular al brazo.
ID:(1416, 0)
Fuerza y torque
Descripción 
Como hemos visto, el torque cumple un rol análogo al de la fuerza en el caso de la rotación:
$F\longleftrightarrow T$
Para establecer las ecuaciones de movimiento, podemos recordar cómo se definió la fuerza en términos del momento:
$F=\displaystyle\frac{\Delta p}{\Delta t}$
y cómo se definió el torque:
$T=\displaystyle\frac{\Delta L}{\Delta t}$
Podemos establecer una relación entre ambas para describir la generación de torque en función de la fuerza:

Por lo tanto, primero debemos definir lo que equivale al momento en el contexto de la rotación.
ID:(325, 0)
Concepto de centro de masa (CM)
Imagen 
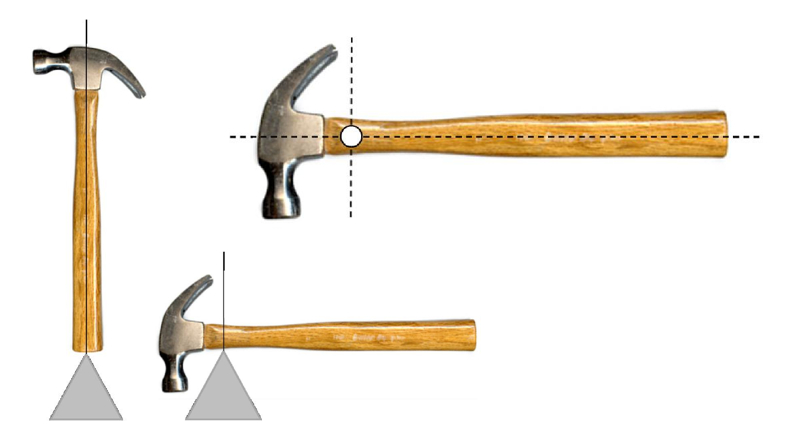
Si uno considera la distribución de masa en el espacio, siempre debería ser posible encontrar un punto en el cual la fuerza ejercida por la masa en un lado sea igual a la fuerza generada en el otro lado:

Este concepto implica que para cualquier orientación de un objeto, se puede encontrar un punto de apoyo en el cual el objeto esté en equilibrio. Cada uno de estos puntos corresponde a una línea vertical. Al repetir este proceso con diferentes orientaciones del objeto, eventualmente se hace evidente que las líneas verticales se cruzan en un punto específico dentro del objeto. A este punto se le denomina centro de masa (CM). En esencia, el centro de masa es el punto único dentro del objeto donde, independientemente de su orientación, siempre se logra el equilibrio.
ID:(323, 0)
Definición del centro de masa (CM)
Imagen 
El centro de masa puede ser definido como el punto en el cual convergen todas las líneas verticales trazadas sobre los puntos en los que el sistema se encuentra en equilibrio:
ID:(11603, 0)
Trayectoria de un cuerpo con traslación y rotación
Imagen 
Cualquier objeto que se mueva y gire lo hace de tal manera que:
• su movimiento de traslación puede ser descrito como el de un objeto donde toda la masa está concentrada en el centro de masa.
• su rotación se lleva a cabo alrededor del centro de masa como si no se estuviera trasladando.

ID:(11604, 0)
Torque, regla de la mano derecha
Imagen 
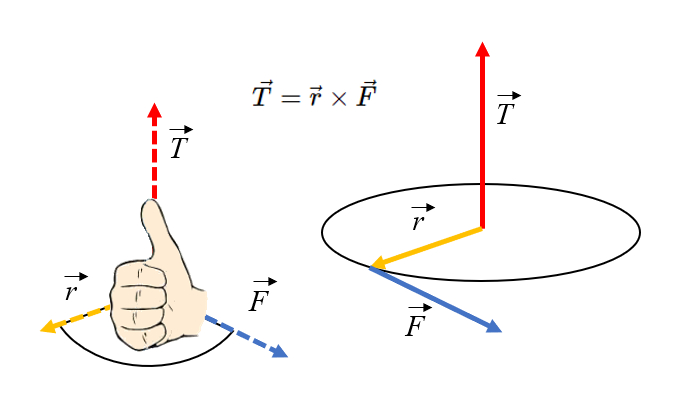
La dirección del torque puede determinarse utilizando la regla de la mano derecha: si los dedos apuntan en la dirección del radio y giramos en la dirección de la fuerza,
ID:(11602, 0)
Generación de Torque
Modelo 
El torque se genera mediante una fuerza aplicada a una cierta distancia del eje de rotación. Fuerzas sobre un punto en el eje de rotación solo llevan a traslación y no inducen cambios en la rotación o torque. La distancia mas corta entre el punto que ataca la fuerza y el eje se denomina brazo y este es siempre perpendicular al eje. Una fuerza paralela al brazo solo genera traslación del eje por lo que solo las fuerzas perpendiculares al brazo son las que generan torque. Finalmente se ve que el torque es mayor mientras mayor es el brazo y mayor es la fuerza perpendicular al brazo.
Variables
Cálculos
Cálculos
Ecuaciones
(ID 3241)
En el caso de una balanza, act a una fuerza gravitacional sobre cada brazo que genera un torque
| $ T = r F $ |
Si la longitud de los brazos es $d_i$ y las fuerzas son $F_i$ con $i=1,2$, la condici n de equilibrio exige que la suma de los torques sea cero:
| $\displaystyle\sum_i \vec{T}_i=0$ |
Por lo tanto, considerando que el signo de cada torque depende de la direcci n en la que est induciendo el giro,
$d_1F_1-d_2F_2=0$
de lo que resulta
| $ d_1 F_1 = d_2 F_2 $ |
.
(ID 3250)
Si se deriva en el tiempo la relaci n para el momento angular
| $ L = r p $ |
para el caso de que el radio sea constante
$T=\displaystyle\frac{dL}{dt}=r\displaystyle\frac{dp}{dt}=rF$
por lo que
| $ T = r F $ |
(ID 4431)
Ejemplos
Como hemos visto, el torque cumple un rol an logo al de la fuerza en el caso de la rotaci n:
$F\longleftrightarrow T$
Para establecer las ecuaciones de movimiento, podemos recordar c mo se defini la fuerza en t rminos del momento:
$F=\displaystyle\frac{\Delta p}{\Delta t}$
y c mo se defini el torque:
$T=\displaystyle\frac{\Delta L}{\Delta t}$
Podemos establecer una relaci n entre ambas para describir la generaci n de torque en funci n de la fuerza:

Por lo tanto, primero debemos definir lo que equivale al momento en el contexto de la rotaci n.
(ID 325)
Si uno considera la distribuci n de masa en el espacio, siempre deber a ser posible encontrar un punto en el cual la fuerza ejercida por la masa en un lado sea igual a la fuerza generada en el otro lado:

Este concepto implica que para cualquier orientaci n de un objeto, se puede encontrar un punto de apoyo en el cual el objeto est en equilibrio. Cada uno de estos puntos corresponde a una l nea vertical. Al repetir este proceso con diferentes orientaciones del objeto, eventualmente se hace evidente que las l neas verticales se cruzan en un punto espec fico dentro del objeto. A este punto se le denomina centro de masa (CM). En esencia, el centro de masa es el punto nico dentro del objeto donde, independientemente de su orientaci n, siempre se logra el equilibrio.
(ID 323)
El centro de masa puede ser definido como el punto en el cual convergen todas las l neas verticales trazadas sobre los puntos en los que el sistema se encuentra en equilibrio:

(ID 11603)
Cualquier objeto que se mueva y gire lo hace de tal manera que:
• su movimiento de traslaci n puede ser descrito como el de un objeto donde toda la masa est concentrada en el centro de masa.
• su rotaci n se lleva a cabo alrededor del centro de masa como si no se estuviera trasladando.

(ID 11604)
La direcci n del torque puede determinarse utilizando la regla de la mano derecha: si los dedos apuntan en la direcci n del radio y giramos en la direcci n de la fuerza,

(ID 11602)
ID:(1416, 0)
