Moment of inertia
Storyboard 
The moment of inertia is the rotating factor that is equivalent to the mass in the translation.
The moment of inertia can be determined empirically by rotating a body around an axis or calculating how the mass is distributed around the axis.
ID:(600, 0)
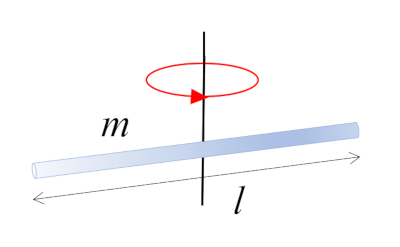
Bar that rotates around an axis $\perp$
Definition 
A bar with mass $m$ and length $l$ rotating around its center, which coincides with the center of mass:
ID:(10962, 0)
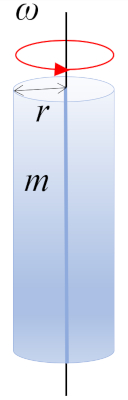
Cylinder rotating around axis $\parallel$
Image 
A rotation of a cylinder with mass $m$ and radius $r$ around the axis of the cylinder, where the center of mass (CM) is located at mid-height:
ID:(10964, 0)
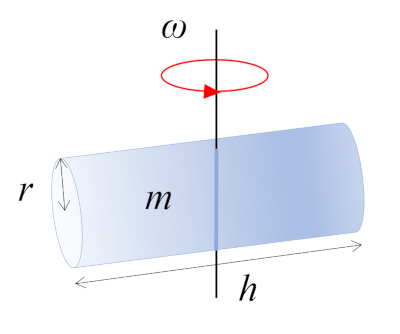
Cylinder that rotates about axis $\perp$
Note 
In this scenario, a cylinder with mass $m$, radius $r$, and height $h$ is rotating around an axis perpendicular to its own axis. This axis passes through the midpoint of the cylinder's length, where the center of mass (CM) is located:
ID:(10965, 0)
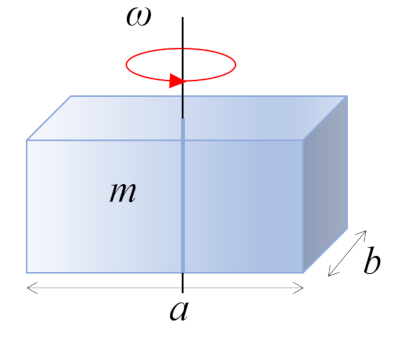
Regular parallelepiped moment of inertia
Quote 
A straight rectangular parallelepiped with mass $m$ and sides $a$ and $b$, perpendicular to the axis of rotation, is rotating around its center of mass, which is located at the geometric center of the body:
ID:(10973, 0)
Straight parallelepiped
Exercise 
In the case of a right rectangular parallelepiped with mass $m$ and side $a$, the center of mass is located at the geometric center:
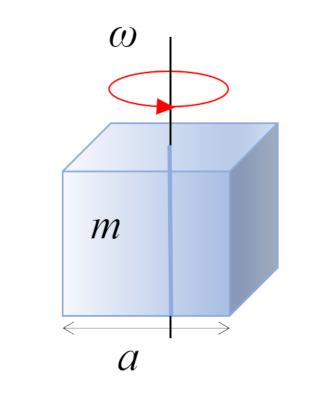
ID:(10963, 0)
Sphere
Equation 
A sphere with mass $m$ and radius $r$ is rotating around its center of mass, which is located at its geometric center:
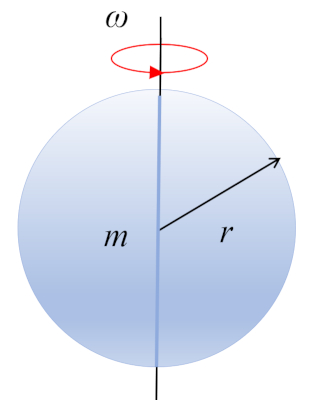
ID:(10490, 0)
