Usuario:
Momento de inercia de un cilindro, eje perpendicular
Storyboard 
El momento de inercia es el equivalente rotacional de la masa en un movimiento de traslación. En el caso de un cilindro que rota alrededor de un eje perpendicular a su propio eje, el caso más simple se presenta cuando la rotación ocurre en torno al centro de masa.
ID:(2087, 0)
Momento de inercia para un eje que no pasa por el centro de masa
Descripción
Cuando el eje de rotación no pasa por el centro de masa (CM), el momento de inercia $I$ puede calcularse mediante el Teorema de Steiner. Para ello, se comienza con el momento de inercia respecto al centro de masa, por ejemplo:
• Para una barra con un eje perpendicular, se tiene
| $ I_{CM} =\displaystyle\frac{1}{12} m l ^2$ |
• Para un cilindro con un eje perpendicular, se tiene
| $ I_{CM} =\displaystyle\frac{1}{12} m ( h ^2+3 r_c ^2)$ |
• Para un cilindro con un eje paralelo, se tiene
| $ I_{CM} =\displaystyle\frac{1}{2} m r_c ^2$ |
• Para un paralelepípedo, se tiene
| $ I_{CM} =\displaystyle\frac{1}{12} m ( a ^2+ b ^2)$ |
• Para un cubo, se tiene
| $ I_{CM} =\displaystyle\frac{1}{6} m a ^2$ |
• Para una esfera, se tiene
| $ I_{CM} =\displaystyle\frac{2}{5} m r_e ^2$ |
Luego, se suma la masa multiplicada por la distancia al cuadrado entre el eje de rotación y el centro de masa
| $ I = I_{CM} + m d ^2$ |
ID:(15867, 0)
Cilindro que rota en torno a eje $\perp$
Imagen
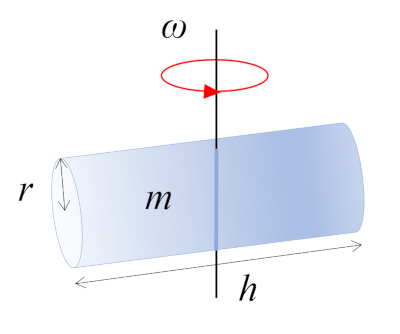
En esta situación, un cilindro con masa $m$, radio $r$ y altura $h$ está girando alrededor de un eje que es perpendicular a su propio eje. Este eje pasa por el punto medio de la longitud del cilindro, donde se localiza el centro de masa (CM):
ID:(10965, 0)
Aplicación del teorema de Steiner para un cilindro, eje $\perp$
Imagen
Para un cilindro con un eje perpendicular al eje del cilindro:
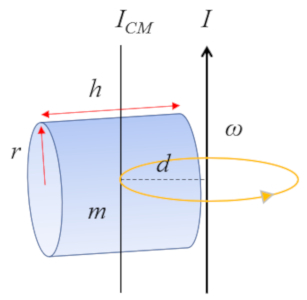
cuyo momento de inercia con respecto al centro de masa (CM) se define como
| $ I_{CM} =\displaystyle\frac{1}{12} m ( h ^2+3 r_c ^2)$ |
el cálculo del momento de inercia se puede realizar utilizando el teorema de Steiner con la siguiente fórmula
| $ I = I_{CM} + m d ^2$ |
.
ID:(11552, 0)
Modelo
Top
Parámetros
Variables
Cálculos
a 
, luego, seleccione la variable: 
a 
Cálculos
Cálculos
Variable 
Dado Calcule 
Objetivo : Ecuación A utilizar 
Ecuaciones
$ I = I_{CM} + m d ^2$
I = I_CM + m * d ^ 2
$ I_{CM} =\displaystyle\frac{1}{12} m ( h ^2+3 r_c ^2)$
I_CM = m * ( h ^ 2 + 3 * r_c ^ 2 ) / 12
$ \omega = \omega_0 + \alpha_0 ( t - t_0 )$
omega = omega_0 + alpha_0 * ( t - t_0 )
$ T = I \alpha_0 $
T = I * alpha
$ T = r F $
T = r * F
$ \theta = \theta_0 + \omega_0 ( t - t_0 )+\displaystyle\frac{1}{2} \alpha_0 ( t - t_0 )^2$
theta = theta_0 + omega_0 *( t - t_0 )+ alpha_0 *( t - t_0 )^2/2
$ \theta = \theta_0 +\displaystyle\frac{ \omega ^2- \omega_0 ^2}{2 \alpha_0 }$
theta = theta_0 +( omega ^2 - omega_0 ^2)/(2* alpha_0 )
ID:(15860, 0)
Momento de inercia de cilindro, eje $\perp$
Ecuación
El momento de inercia de un cilindro que gira alrededor de un eje perpendicular ($\perp$) que pasa por el centro se calcula al dividir el cuerpo en pequeños volúmenes y sumarlos:
| $ I =\displaystyle\int_V r ^2 \rho dV $ |
lo que resulta en
| $ I_{CM} =\displaystyle\frac{1}{12} m ( h ^2+3 r_c ^2)$ |
.
ID:(4435, 0)
Teorema de Steiner
Ecuación
El momento de inercia para eje que no pasa por el CM ($I$) se puede calcular utilizando el momento de inercia del centro de masa ($I_{CM}$) y sumándole el momento de inercia de la masa del cuerpo ($m$) como si fuera una masa puntual en la distancia centro de masa y eje ($d$):
| $ I = I_{CM} + m d ^2$ |
ID:(3688, 0)
Relación simple torque - fuerza
Ecuación
Dado que la relación entre el momento angular y el momento es
| $ L = r p $ |
su derivada temporal nos conduce a la relación de torque
| $ T = r F $ |
Si se deriva en el tiempo la relación para el momento angular
| $ L = r p $ |
para el caso de que el radio sea constante
$T=\displaystyle\frac{dL}{dt}=r\displaystyle\frac{dp}{dt}=rF$
por lo que
| $ T = r F $ |
La rotación del cuerpo tiene lugar alrededor de un eje en la dirección del torque, que atraviesa el centro de masa.
ID:(4431, 0)
Torque para momento de inercia constante
Ecuación
En el escenario en el que el momento de inercia es constante, la derivada del momento angular es igual a
| $ L = I \omega $ |
lo cual implica que el torque es igual a
| $ T = I \alpha_0 $ |
| $ T = I \alpha $ |
Dado que el momento es igual a
| $ L = I \omega $ |
se sigue que en el caso en que el momento de inercia no cambia con el tiempo,
$T=\displaystyle\frac{dL}{dt}=\displaystyle\frac{d}{dt}(I\omega) = I\displaystyle\frac{d\omega}{dt} = I\alpha$
lo que implica que
| $ T = I \alpha $ |
.
Esta relación equivale a la segunda ley de Newton en el contexto de la rotación en lugar de la traslación.
ID:(3253, 0)
Velocidad angular con aceleración angular constante
Ecuación
Con la aceleración angular constante ($\alpha_0$), la velocidad angular ($\omega$) establece una relación lineal con el tiempo ($t$), que también incorpora las variables la velocidad angular inicial ($\omega_0$) y el tiempo inicial ($t_0$), tal que:
| $ \omega = \omega_0 + \alpha_0 ( t - t_0 )$ |
Si suponemos que la aceleración angular media ($\bar{\alpha}$) es constante, equivalente a la aceleración angular constante ($\alpha_0$), entonces se aplica la siguiente ecuación:
| $ \bar{\alpha} = \alpha_0 $ |
Por lo tanto, al considerar la diferencia de velocidades angulares ($\Delta\omega$) junto con la velocidad angular ($\omega$) y la velocidad angular inicial ($\omega_0$):
| $ \Delta\omega = \omega - \omega_0 $ |
y el tiempo transcurrido ($\Delta t$) en relación con el tiempo ($t$) y el tiempo inicial ($t_0$):
| $ \Delta t \equiv t - t_0 $ |
la ecuación para la aceleración angular media ($\bar{\alpha}$):
| $ \bar{\alpha} \equiv \displaystyle\frac{ \Delta\omega }{ \Delta t }$ |
puede expresarse como:
$\alpha_0 = \alpha = \displaystyle\frac{\Delta \omega}{\Delta t} = \displaystyle\frac{\omega - \omega_0}{t - t_0}$
Despejando esta última, obtenemos:
| $ \omega = \omega_0 + \alpha_0 ( t - t_0 )$ |
Esta ecuación representa una recta en el plano de velocidad angular versus tiempo.
ID:(3237, 0)
Angulo para aceleración angular constante
Ecuación
Dado que el desplazamiento total corresponde al área bajo la curva de velocidad angular frente al tiempo, en el caso de una aceleración angular constante ($\alpha_0$), se determina que el desplazamiento el ángulo ($\theta$) con las variables el ángulo inicial ($\theta_0$), el tiempo ($t$), el tiempo inicial ($t_0$) y la velocidad angular inicial ($\omega_0$) es el siguiente:
| $ \theta = \theta_0 + \omega_0 ( t - t_0 )+\displaystyle\frac{1}{2} \alpha_0 ( t - t_0 )^2$ |
En el caso de la aceleración angular constante ($\alpha_0$), la velocidad angular ($\omega$) en función de el tiempo ($t$) sigue una relación lineal con el tiempo inicial ($t_0$) y la velocidad angular inicial ($\omega_0$) de la forma:
| $ \omega = \omega_0 + \alpha_0 ( t - t_0 )$ |
Dado que el ángulo recorrido es igual al área bajo la curva de velocidad angular-tiempo, en este caso se puede sumar la contribución del rectángulo:
$\omega_0(t-t_0)$
y el triángulo:
$\displaystyle\frac{1}{2}\alpha_0(t-t_0)^2$
Esto nos lleva a la expresión para el ángulo ($\theta$) y el ángulo inicial ($\theta_0$):
| $ \theta = \theta_0 + \omega_0 ( t - t_0 )+\displaystyle\frac{1}{2} \alpha_0 ( t - t_0 )^2$ |
Esta expresión corresponde a la forma general de una parábola.
ID:(3682, 0)
Angulo de frenado en función de la velocidad angular
Ecuación
En el caso de la aceleración angular constante ($\alpha_0$), la función de la velocidad angular ($\omega$) respecto a el tiempo ($t$), con variables adicionales la velocidad angular inicial ($\omega_0$) y el tiempo inicial ($t_0$), está expresada por la ecuación:
| $ \omega = \omega_0 + \alpha_0 ( t - t_0 )$ |
A partir de esta ecuación, es posible calcular la relación entre el ángulo ($\theta$) y el ángulo inicial ($\theta_0$), así como el cambio en la velocidad angular:
| $ \theta = \theta_0 +\displaystyle\frac{ \omega ^2- \omega_0 ^2}{2 \alpha_0 }$ |
Si resolvemos la ecuación de la velocidad angular ($\omega$) en términos de tiempo, que incluye las variables la velocidad angular inicial ($\omega_0$), el tiempo ($t$), el tiempo inicial ($t_0$) y la aceleración angular constante ($\alpha_0$):
| $ \omega = \omega_0 + \alpha_0 ( t - t_0 )$ |
obtenemos la siguiente expresión para el tiempo:
$t - t_0 = \displaystyle\frac{\omega - \omega_0}{\alpha_0}$
Esta solución puede ser sustituida en la ecuación para calcular el ángulo ($\theta$) utilizando el ángulo inicial ($\theta_0$) de la siguiente manera:
| $ \theta = \theta_0 + \omega_0 ( t - t_0 )+\displaystyle\frac{1}{2} \alpha_0 ( t - t_0 )^2$ |
Lo que resulta en la siguiente ecuación:
| $ \theta = \theta_0 +\displaystyle\frac{ \omega ^2- \omega_0 ^2}{2 \alpha_0 }$ |
ID:(4386, 0)