Diagrama en espacio momento-posición $p-q$
Definición 
Una técnica para analizar el movimiento consiste en representar el momento en función de la posición de un cuerpo en movimiento. Esta representación nos permite estudiar cómo evoluciona el momento en relación con la posición alcanzada.
La representación del movimiento en el espacio momento-posición $p-q$ nos permite analizar la evolución del desplazamiento, resaltando los extremos en la posición y el momento.
En el caso de un movimiento periódico o cuando consideramos el trayecto de ida y vuelta, esto puede representarse de la siguiente manera:
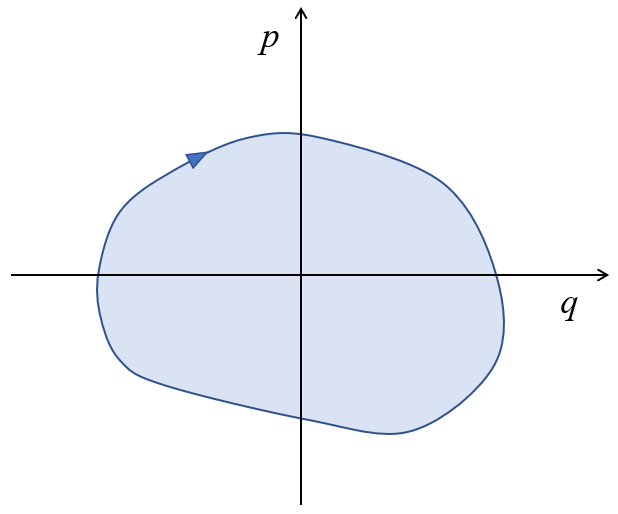
Adicionalmente, se puede observar que el área encerrada por la curva
$\displaystyle\int_{q_1}^{q_2} p dq = \displaystyle\int_{v_1}^{v_2} m v dv = \displaystyle\frac{1}{2} m v_2^2 - \displaystyle\frac{1}{2} m v_1^2$
corresponde a la energía del sistema.
El área encerrada por la curva en el diagrama momento-posición $p-q$ corresponde a la energía del sistema.
ID:(1240, 0)
Espacio de Fase
Descripción 
Variables
Cálculos
Cálculos
Ecuaciones
Dado que la energ a cin tica es
| $ K =\displaystyle\frac{ p ^2}{2 m_i }$ |
y la energ a potencial es
| $ V = - \displaystyle\frac{ G m_g M }{ r } $ |
podemos expresar la energ a en funci n del radio representado por la variable $q$ de la siguiente manera
| $ E_G = \displaystyle\frac{ p ^2}{2 m_i } - \displaystyle\frac{ G m_g M }{ q }$ |
En el caso en que la energ a cin tica supere la energ a potencial en el radio de inicio y la energ a sea positiva (indicando que el objeto puede escapar del planeta), la ecuaci n se puede escribir como
$1 = \left(\displaystyle\frac{p}{\sqrt{2mE}}\right)^2 - \displaystyle\frac{GmM}{Eq}$
lo cual simplifica a
$y=\pm\sqrt{1+\displaystyle\frac{1}{x}}$
con
$x=\displaystyle\frac{q}{GmM/E}$
, y
$y=\displaystyle\frac{p}{2mE}$
En el caso en que la energ a cin tica no supere la energ a potencial (indicando que el objeto no puede escapar de la atracci n del planeta), la energ a es negativa, y la expresi n se escribe como
$1 = -\left(\displaystyle\frac{p}{\sqrt{2mE}}\right)^2 + \displaystyle\frac{GmM}{Eq}$
donde $E$ es el valor absoluto de la energ a. Con las definiciones de $x$ e $y", tenemos
$y=\pm\sqrt{\displaystyle\frac{1}{x}-1}$
(ID 1185)
La energ a cin tica en funci n del momento est dada por
| $ K =\displaystyle\frac{ p ^2}{2 m_i }$ |
y la energ a potencial en funci n de la altura se expresa como
| $ V =\displaystyle\frac{1}{2} k x ^2$ |
Por lo tanto, si expresamos la elongaci n como la posici n
$x = q$
obtenemos
| $ E_s =\displaystyle\frac{ p ^2}{2 m_i }+\displaystyle\frac{ k }{2} q ^2$ |
(ID 1187)
Dado que la energ a cin tica es igual a
| $ K_t =\displaystyle\frac{1}{2} m_i v ^2$ |
y el momento es
| $ p = m_i v $ |
podemos expresarlo como
$K_t=\displaystyle\frac{1}{2} m_i v^2=\displaystyle\frac{1}{2} m_i \left(\displaystyle\frac{p}{m_i}\right)^2=\displaystyle\frac{p^2}{2m_i}$
es decir,
| $ K =\displaystyle\frac{ p ^2}{2 m_i }$ |
(ID 4425)
Como la energ a cin tica en funci n del momento es
| $ K =\displaystyle\frac{ p ^2}{2 m_i }$ |
y la energ a potencial en funci n de la altura es
| $ V = - m_g g z $ |
por lo que si expresamos la altura como la posici n
$h = q$
obtenemos
| $ E =\displaystyle\frac{ p ^2}{2 m_i }+ m_g g q $ |
(ID 4426)
Dado que en general la energ a es la suma de la energ a cin tica
| $ K =\displaystyle\frac{ p ^2}{2 m_i }$ |
y la energ a potencial
$E=\displaystyle\frac{p^2}{2m}+U$
Si despejamos el momento, obtenemos la siguiente expresi n:
| $ p =\pm\sqrt{2 m ( E - U )}$ |
(ID 4429)
Ejemplos
Una t cnica para analizar el movimiento consiste en representar el momento en funci n de la posici n de un cuerpo en movimiento. Esta representaci n nos permite estudiar c mo evoluciona el momento en relaci n con la posici n alcanzada.
La representaci n del movimiento en el espacio momento-posici n $p-q$ nos permite analizar la evoluci n del desplazamiento, resaltando los extremos en la posici n y el momento.
En el caso de un movimiento peri dico o cuando consideramos el trayecto de ida y vuelta, esto puede representarse de la siguiente manera:

Adicionalmente, se puede observar que el rea encerrada por la curva
$\displaystyle\int_{q_1}^{q_2} p dq = \displaystyle\int_{v_1}^{v_2} m v dv = \displaystyle\frac{1}{2} m v_2^2 - \displaystyle\frac{1}{2} m v_1^2$
corresponde a la energ a del sistema.
El rea encerrada por la curva en el diagrama momento-posici n $p-q$ corresponde a la energ a del sistema.
(ID 1240)
La energ a cin tica de una masa $m$
| $ K_t =\displaystyle\frac{1}{2} m_i v ^2$ |
puede expresarse en funci n del momento como
| $ K =\displaystyle\frac{ p ^2}{2 m_i }$ |
(ID 4425)
Si despejamos la energ a en funci n del momento, obtenemos las expresiones para el momento positivo y negativo:
| $ p =\pm\sqrt{2 m ( E - U )}$ |
(ID 4429)
Para el caso de una part cula en el campo gravitacional de la Tierra, la energ a en funci n del momento $p$ y la posici n $q$ es
| $ E =\displaystyle\frac{ p ^2}{2 m_i }+ m_g g q $ |
La ecuaci n puede ser escrita en forma adimensional de la siguiente manera
$y=\pm\sqrt{1-x}$
con
$x=\displaystyle\frac{q}{mg/E}$
, y
$y=\displaystyle\frac{p}{\sqrt{2mE}}$
lo cual se representa a continuaci n

(ID 4426)
Para el caso de una masa oscilando con un resorte, la energ a en funci n del momento $p$ y posici n $q$ es
| $ E_s =\displaystyle\frac{ p ^2}{2 m_i }+\displaystyle\frac{ k }{2} q ^2$ |
La ecuaci n puede expresarse en forma adimensional como
$1=y^2 + x^2$
donde
$x=\displaystyle\frac{q}{\sqrt{2E/k}}$
, y
$y=\displaystyle\frac{p}{\sqrt{2m_iE}}$
resolviendo para
$y=\pm\sqrt{1-x^2}$
Su representaci n en el plano xy se muestra a continuaci n
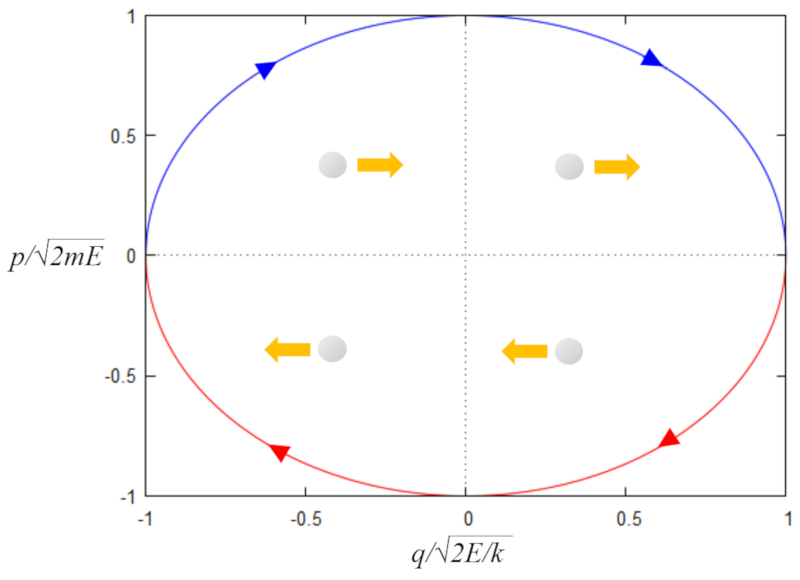
(ID 1187)
Para el caso de una masa en un campo gravitacional, la energ a en funci n del momento
| $ E_G = \displaystyle\frac{ p ^2}{2 m_i } - \displaystyle\frac{ G m_g M }{ q }$ |
La ecuaci n se puede expresar en forma adimensional para el caso de energ a positiva de la siguiente manera (curvas azules y verdes):
$y=\pm\sqrt{1+\displaystyle\frac{1}{x}}$
Y para el caso de energ a negativa, se expresa de la siguiente manera (curvas rojas y violetas):
$y=\pm\sqrt{\displaystyle\frac{1}{x}-1}$
Donde
$x=\displaystyle\frac{q}{GmM/E}$
, y
$y=\displaystyle\frac{p}{2mE}$
Lo cual se representa a continuaci n:

(ID 1185)
ID:(1659, 0)
