Utilisateur:
Énergie cinétique de rotation et moments d'inertie
Storyboard 
L'énergie cinétique de rotation est une fonction de la vitesse angulaire atteinte grâce à l'application d'un couple pendant un certain temps tout en parcourant un angle donné.
Ainsi, l'énergie cinétique de rotation est proportionnelle au moment d'inertie de l'objet et au carré de la vitesse angulaire.
ID:(1417, 0)
Moment d'inertie
Storyboard
En dynamique rotationnelle, le moment dinertie joue un rôle équivalent à celui de la masse inerte en translation. Cependant, contrairement à la masse, le moment dinertie dépend de la géométrie du corps et de la façon dont sa masse est répartie par rapport à laxe de rotation. Son calcul est donc indispensable pour chaque situation que lon souhaite modéliser.
Variables
Calculs
à 
,
puis, sélectionnez la variable: 
à 
Calculs
Variable
Donnée
Calculer
Cible :
Équation
À utiliser
Équations
A écart de travail ($\Delta W$) nécessaire pour quun objet passe de a vitesse angulaire initiale ($\omega_0$) à A vitesse angulaire ($\omega$) est obtenue en appliquant un a torque ($T$) qui produit un déplacement angulaire a différence d'angles ($\Delta\theta$), selon :
En appliquant la deuxième loi de Newton pour la rotation, avec a moment d\'inertie de l\'axe qui ne passe pas par le CM ($I$) et a accélération angulaire moyenne ($\bar{\alpha}$) :
cette expression peut être réécrite comme :
$\Delta W = I \alpha \Delta\theta$
ou, en utilisant a différence de vitesses angulaires ($\Delta\omega$) et le temps écoulé ($\Delta t$) :
nous obtenons :
$\Delta W = I\displaystyle\frac{\Delta\omega}{\Delta t} \Delta\theta$
En utilisant la définition de a vitesse angulaire moyenne ($\bar{\omega}$) et le temps écoulé ($\Delta t$) :
il en résulte :
$\Delta W = I\displaystyle\frac{\Delta\omega}{\Delta t} \Delta\theta = I\omega \Delta\omega$
où A différence de vitesses angulaires ($\Delta\omega$) sexprime comme :
Dautre part, la vitesse angulaire peut être approximée par la vitesse angulaire moyenne :
$\bar{\omega}=\displaystyle\frac{\omega_1 + \oemga_2}{2}$
En combinant les deux expressions, on obtient léquation :
$\Delta W = I \omega \Delta\omega = I(\omega_2 - \omega_1) \displaystyle\frac{(\omega_1 + \omega_2)}{2} = \displaystyle\frac{I}{2}(\omega_2^2 - \omega_1^2)$
Ainsi, la variation dénergie sexprime comme :
$\Delta W = \displaystyle\frac{I}{2}\omega_2^2 - \displaystyle\frac{I}{2}\omega_1^2$
Cela permet de définir lénergie cinétique de rotation comme :
Le moment d'inertie d'une barre en rotation autour d'un axe perpendiculaire ($\perp$) passant par le centre est obtenu en divisant le corps en petits volumes et en les additionnant :
ce qui aboutit
Le moment d'inertie d'un parall l pip de en rotation autour d'un axe passant par son centre est obtenu en divisant le corps en petits volumes et en les additionnant :
ce qui aboutit
Le moment d'inertie d'un cylindre en rotation autour d'un axe parall le ($\parallel$) son axe central est obtenu en segmentant le corps en petits volumes et en les additionnant :
ce qui aboutit
Le moment d'inertie d'un cylindre en rotation autour d'un axe perpendiculaire ($\perp$) passant par le centre est obtenu en divisant le corps en petits volumes et en les additionnant :
ce qui aboutit
Le moment d'inertie d'une sph re en rotation autour d'un axe passant par son centre est obtenu en segmentant le corps en petits volumes et en les additionnant :
ce qui donne comme r sultat :
Exemples
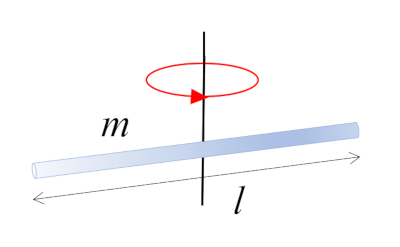
Une barre de masse $m$ et de longueur $l$ qui tourne autour de son centre, qui co ncide avec le centre de masse :
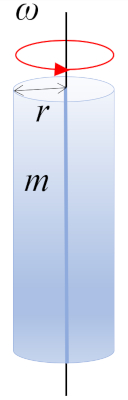
Consid rons une rotation d'un cylindre de masse $m$ et de rayon $r$ autour de l'axe du cylindre, o le centre de masse (CM) se situe mi-hauteur :
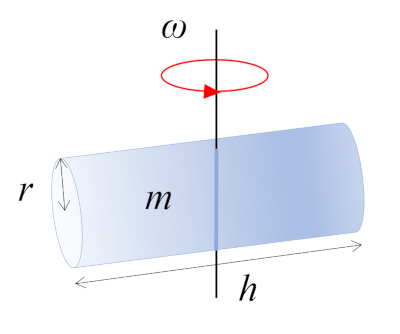
Dans cette situation, un cylindre avec une masse $m$, un rayon $r$ et une hauteur $h$ tourne autour d'un axe perpendiculaire son propre axe. Cet axe passe par le milieu de la longueur du cylindre, o se trouve le centre de masse (CM) :
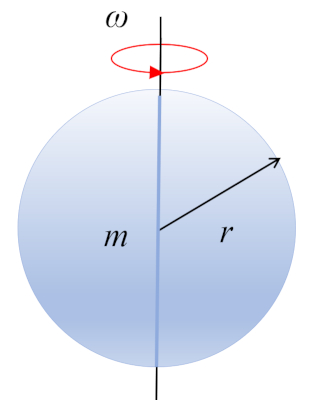
Une sph re de masse $m$ et de rayon $r$ tourne autour de son centre de masse, qui est situ au centre de celle-ci :
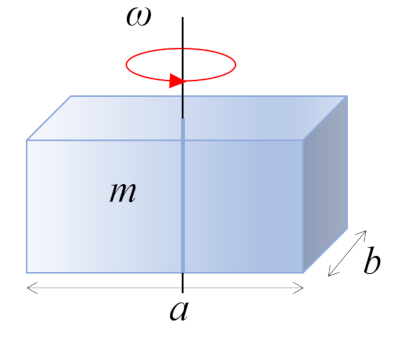
Un parall l pip de rectangle de masse $m$ et de c t s $a$ et $b$, perpendiculaire l'axe de rotation, tourne autour de son centre de masse, qui se trouve au centre g om trique du corps:
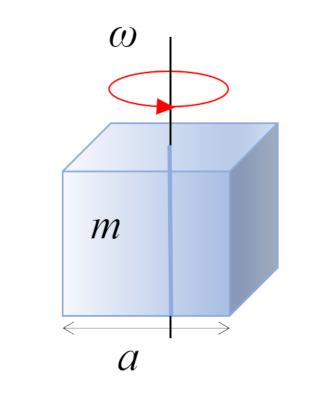
Dans le cas d'un parall l pip de rectangle avec une masse $m$ et un c t $a$, le centre de masse se situe au centre g om trique :
A moment d\'inertie de l\'axe qui ne passe pas par le CM ($I$) peut tre calcul en utilisant a moment d\'inertie du centre de masse ($I_{CM}$) et en ajoutant le moment d'inertie de a masse corporelle ($m$) comme s'il s'agissait d'une masse ponctuelle a distance centre de masse et axe ($d$) :
A moment d\'inertie CM d\'une barre mince, axe perpendiculaire ($I_{CM}$) est obtenu en fonction de a masse corporelle ($m$) et a longueur de barre mince ($l$) :
A moment d\'inertie CM d\'un cylindre, axe parallèle à l\'axe du cylindre ($I_{CM}$) est obtenu en fonction de a masse corporelle ($m$) et a rayon du cylindre ($r_c$) :
ERROR:5325 est obtenu en fonction de a masse corporelle ($m$), a hauteur du cylindre ($h$) et a rayon du cylindre ($r_c$) :
A moment d\'inertie CM d\'une barre mince, axe perpendiculaire ($I_{CM}$) est obtenu en fonction de a masse corporelle ($m$), a longueur d\'arête d\'un parallélépipède rectangle ($a$) et a largeur du bord d\'un parallélépipède droit ($b$) :
A moment d\'inertie CM d\'une sphère ($I_{CM}$) est obtenu en fonction de a masse corporelle ($m$) et a rayon de la sphère ($r_e$) :
A énergie cinétique de rotation ($K_r$) est une fonction de a vitesse angulaire ($\omega$) et dune mesure de linertie représentée par a moment d\'inertie de l\'axe qui ne passe pas par le CM ($I$) :
ID:(1417, 0)
