Velocidad constante, dos etapas
Storyboard 
Si durante un movimiento a velocidad constante se produce un cambio en esta, se obtiene un movimiento que ocurre en dos etapas, cada una caracterizada por una velocidad definida.
Cada etapa se modela con una relación lineal representada por una recta, donde la clave radica en que el tiempo y la posición final de la primera etapa son, a su vez, el tiempo y la posición inicial de la segunda etapa.
Es importante notar que este modelo presenta un problema, ya que la velocidad cambia de forma instantánea, lo que equivale a una aceleración seguida de un frenado infinito, lo cual no es realista. Sin embargo, este problema no resulta relevante si la duración de las etapas es considerablemente más larga que el tiempo en el que ocurre el cambio de velocidad.
ID:(1448, 0)
Velocidad constante, dos etapas
Descripción 
Si durante un movimiento a velocidad constante se produce un cambio en esta, se obtiene un movimiento que ocurre en dos etapas, cada una caracterizada por una velocidad definida.
Cada etapa se modela con una relación lineal representada por una recta, donde la clave radica en que el tiempo y la posición final de la primera etapa son, a su vez, el tiempo y la posición inicial de la segunda etapa.
Variables
Cálculos
Cálculos
Ecuaciones
Con la distancia recorrida en un tiempo ($\Delta s$) es con la posición ($s$) y la posición inicial ($s_0$):
| $ \Delta s = s - s_0 $ |
y el tiempo transcurrido ($\Delta t$) es con el tiempo ($t$) y el tiempo inicial ($t_0$):
| $ \Delta t \equiv t - t_0 $ |
Se tiene que la ecuaci n de la velocidad media:
| $ v_0 \equiv\displaystyle\frac{ \Delta s }{ \Delta t }$ |
puede escribirse como:
$v_0 = \bar{v} = \displaystyle\frac{\Delta s}{\Delta t} = \displaystyle\frac{s - s_0}{t - t_0}$
Por lo tanto, despejando, se obtiene:
| $ s = s_0 + v_0 ( t - t_0 )$ |
(ID 3154)
Con la distancia recorrida en un tiempo ($\Delta s$) es con la posición ($s$) y la posición inicial ($s_0$):
| $ \Delta s = s - s_0 $ |
y el tiempo transcurrido ($\Delta t$) es con el tiempo ($t$) y el tiempo inicial ($t_0$):
| $ \Delta t \equiv t - t_0 $ |
Se tiene que la ecuaci n de la velocidad media:
| $ v_0 \equiv\displaystyle\frac{ \Delta s }{ \Delta t }$ |
puede escribirse como:
$v_0 = \bar{v} = \displaystyle\frac{\Delta s}{\Delta t} = \displaystyle\frac{s - s_0}{t - t_0}$
Por lo tanto, despejando, se obtiene:
| $ s = s_0 + v_0 ( t - t_0 )$ |
(ID 3154)
Si se parte de la posición inicial ($s_0$) y se desea calcular la distancia recorrida en un tiempo ($\Delta s$), es necesario definir un valor para la posición ($s$).
En un sistema unidimensional, la distancia recorrida en un tiempo ($\Delta s$) se obtiene simplemente restando la posición inicial ($s_0$) de la posición ($s$), lo que da como resultado:
| $ \Delta s = s - s_0 $ |
(ID 4352)
Si se parte de la posición inicial ($s_0$) y se desea calcular la distancia recorrida en un tiempo ($\Delta s$), es necesario definir un valor para la posición ($s$).
En un sistema unidimensional, la distancia recorrida en un tiempo ($\Delta s$) se obtiene simplemente restando la posición inicial ($s_0$) de la posición ($s$), lo que da como resultado:
| $ \Delta s = s - s_0 $ |
(ID 4352)
Ejemplos
El modelo de velocidad constante describe el movimiento durante una etapa o intervalo de tiempo en el que la velocidad del objeto puede considerarse constante. Sin embargo, un movimiento m s complejo puede incluir varias etapas o intervalos en los que la velocidad var a e incluso puede invertirse (volverse negativa), lo que indica que el cuerpo se devuelve.
Si se ensamblan dos modelos de velocidad constante como movimientos consecutivos, se pueden vincular considerando que las posiciones y los tiempos finales de la primera etapa coinciden con las posiciones y los tiempos iniciales del segundo movimiento. As , se definen las distancias la distancia recorrida en la primera la etapa ($\Delta s_1$) y la distancia recorrida en la segunda la etapa ($\Delta s_2$), recorridas con las velocidades la velocidad primera etapa ($v_1$) y la velocidad segunda etapa ($v_2$). Estos valores pueden modificarse, incluso invirtiendo el movimiento, mediante la asignaci n de velocidades negativas y ejecutando la simulaci n con el bot n 'start'.
(ID 15383)
Un cuerpo se puede desplazar a la velocidad primera etapa ($v_1$) y luego pasa luego a una la velocidad segunda etapa ($v_2$). Con ello pasa a una nueva etapa siendo necesario poder describir ambas en forma matematica para poder predecir su movimiento.
La clave es ver que ambas etapas tienen un punto en comun que se caracteriza por:
• el posición final primera e inició segunda etapa ($s_1$) que es la posici n final de la primera y el inicio de la segunda etapa.
• el tiempo final primera e inició segunda etapa ($t_1$) que es el tiempo final de la primera y el inicio de la segunda etapa.
Con ello los diagramas de la posici n en el tiempo pueden ser acopladas como puesta la siguiente representaci n:
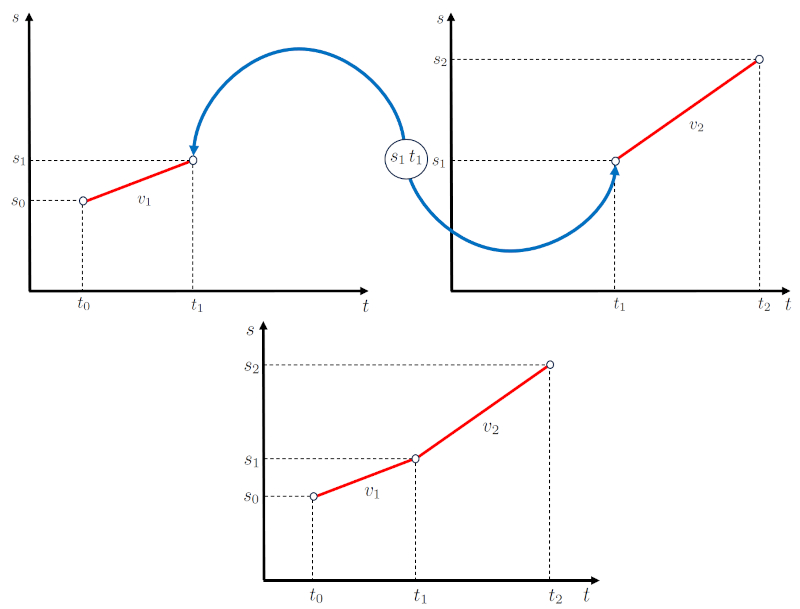
En ella se tiene un punto inicial de la primera etapa caracterizado por la posición inicial ($s_0$) y el tiempo inicial ($t_0$) y el punto final de la segunda etapa caracterizado por la posición final segunda etapa ($s_2$) y el tiempo que finaliza segunda etapa ($t_2$).
(ID 15504)
En un escenario de movimiento en dos etapas, primero el objeto avanza una distancia de una distancia recorrida en la primera la etapa ($\Delta s_1$) durante un lapso de tiempo de un tiempo transcurrido en la primera etapa ($\Delta t_1$) con una velocidad de una velocidad primera etapa ($v_1$).
| $ v_1 \equiv\displaystyle\frac{ \Delta s_1 }{ \Delta t_1 }$ |
Posteriormente, en la segunda etapa, avanza una distancia de una distancia recorrida en la segunda la etapa ($\Delta s_2$) durante un per odo de tiempo de un tiempo transcurrido en la segunda etapa ($\Delta t_2$) con una velocidad de una velocidad segunda etapa ($v_2$).
| $ v_2 \equiv\displaystyle\frac{ \Delta s_2 }{ \Delta t_2 }$ |
Al representar esto gr ficamente, obtenemos un diagrama de posici n y tiempo como se muestra a continuaci n:
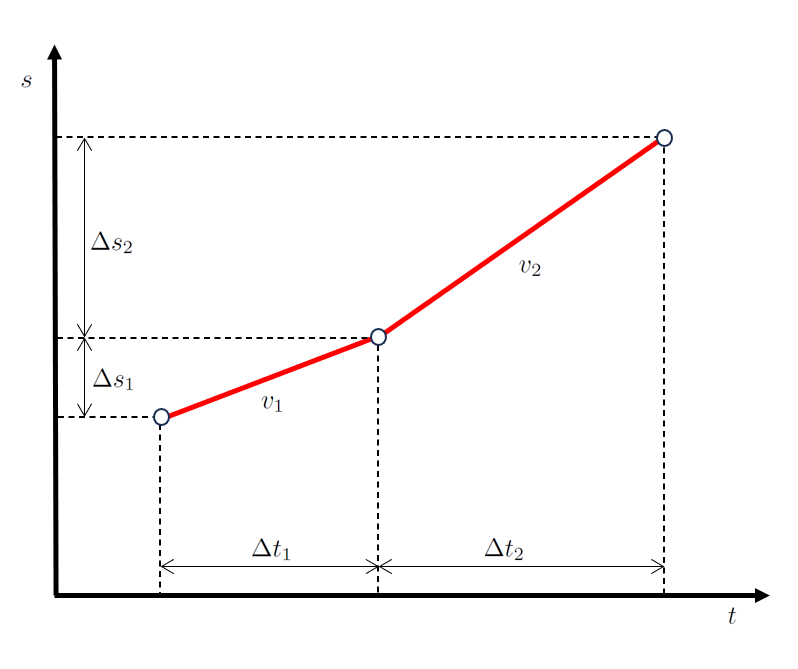
La clave aqu es que los valores el tiempo transcurrido en la primera etapa ($\Delta t_1$) y el tiempo transcurrido en la segunda etapa ($\Delta t_2$) son secuenciales, al igual que los valores la distancia recorrida en la primera la etapa ($\Delta s_1$) y la distancia recorrida en la segunda la etapa ($\Delta s_2$).
(ID 15395)
En el caso de un movimiento en dos etapas, la primera etapa se puede describir mediante una funci n que involucra los puntos el tiempo inicial ($t_0$), el tiempo final primera e inició segunda etapa ($t_1$), la posición inicial ($s_0$) y el posición final primera e inició segunda etapa ($s_1$), representada por una recta con pendiente de la velocidad primera etapa ($v_1$):
| $ s_1 = s_0 + v_1 ( t_1 - t_0 )$ |
Para la segunda etapa, definida por los puntos el posición final primera e inició segunda etapa ($s_1$), la posición final segunda etapa ($s_2$), el tiempo final primera e inició segunda etapa ($t_1$) y el tiempo que finaliza segunda etapa ($t_2$), se emplea una segunda recta con pendiente de la velocidad segunda etapa ($v_2$):
| $ s_2 = s_1 + v_2 ( t_2 - t_1 )$ |
que se representa como:
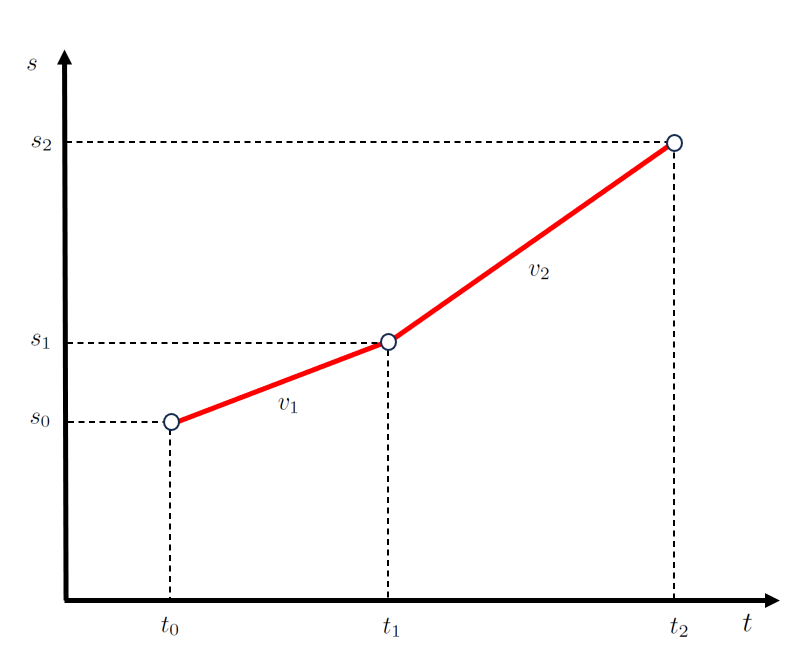
Es importante notar que el inicio de la segunda etapa, definido por los puntos el tiempo final primera e inició segunda etapa ($t_1$) y el posición final primera e inició segunda etapa ($s_1$), coincide con el final de la primera etapa.
(ID 15396)
El modelo base implica dos movimientos en etapas consecutivas.
En la primera etapa, se parte de la posición inicial ($s_0$) y se termina en el posición final primera e inició segunda etapa ($s_1$), cubriendo una distancia de la distancia recorrida en la primera la etapa ($\Delta s_1$), que se inicia en el tiempo inicial ($t_0$) y termina en el tiempo final primera e inició segunda etapa ($t_1$), con una duraci n de el tiempo transcurrido en la primera etapa ($\Delta t_1$) y una velocidad de la velocidad primera etapa ($v_1$).
En la segunda etapa, se inicia en el posición final primera e inició segunda etapa ($s_1$) y termina en la posición final segunda etapa ($s_2$), cubriendo una distancia de la distancia recorrida en la segunda la etapa ($\Delta s_2$), que se inicia en el tiempo final primera e inició segunda etapa ($t_1$) y termina en el tiempo que finaliza segunda etapa ($t_2$), con una duraci n de la distancia recorrida en la segunda la etapa ($\Delta s_2$) y una velocidad de la velocidad segunda etapa ($v_2$).
El diagrama resultante consta de dos subdiagramas en los que se viaja a una velocidad constante. Ambos diagramas est n conectados por el posición final primera e inició segunda etapa ($s_1$) y el tiempo final primera e inició segunda etapa ($t_1$), que corresponden al punto final de la primera etapa y al punto inicial de la segunda.

Con esto, la estructura de red del modelo es la siguiente:
(ID 15384)
ID:(1448, 0)
