Konstante Geschwindigkeit, zwei Stufen
Storyboard 
Wenn während einer Bewegung mit konstanter Geschwindigkeit eine Änderung auftritt, ergibt sich eine Bewegung, die in zwei Etappen stattfindet, jede gekennzeichnet durch eine definierte Geschwindigkeit.
Jede Etappe wird mit einer linearen Beziehung modelliert, die durch eine Linie dargestellt wird, wobei der Schlüssel darin besteht, dass die endgültige Zeit und Position der ersten Etappe wiederum die Anfangszeit und -position der zweiten Etappe sind.
Es ist wichtig zu beachten, dass dieses Modell ein Problem aufweist, da die Geschwindigkeit sich sofort ändert, was einer Beschleunigung und anschließend einer unendlichen Verzögerung entspricht, was unrealistisch ist. Allerdings ist dieses Problem nicht relevant, wenn die Dauer der Phasen wesentlich länger ist als die Zeit, in der die Geschwindigkeitsänderung erfolgt.
ID:(1448, 0)
Konstante Geschwindigkeit, zwei Stufen
Beschreibung 
Wenn während einer Bewegung mit konstanter Geschwindigkeit eine Änderung auftritt, ergibt sich eine Bewegung, die in zwei Etappen stattfindet, jede gekennzeichnet durch eine definierte Geschwindigkeit.
Jede Etappe wird mit einer linearen Beziehung modelliert, die durch eine Linie dargestellt wird, wobei der Schlüssel darin besteht, dass die endgültige Zeit und Position der ersten Etappe wiederum die Anfangszeit und -position der zweiten Etappe sind.
Variablen
Berechnungen
Berechnungen
Gleichungen
Mit die Zurückgelegte Strecke in einer Zeit ($\Delta s$) gleich die Position ($s$) und die Ausgangsstellung ($s_0$):
| $ \Delta s = s - s_0 $ |
und der Abgelaufene Zeit ($\Delta t$) ist gleich der Zeit ($t$) und der Startzeit ($t_0$):
| $ \Delta t \equiv t - t_0 $ |
Die Gleichung f r die durchschnittliche Geschwindigkeit:
| $ v_0 \equiv\displaystyle\frac{ \Delta s }{ \Delta t }$ |
kann geschrieben werden als:
$v_0 = \bar{v} = \displaystyle\frac{\Delta s}{\Delta t} = \displaystyle\frac{s - s_0}{t - t_0}$
somit ergibt sich, wenn man nach ihr aufl st:
| $ s = s_0 + v_0 ( t - t_0 )$ |
(ID 3154)
Mit die Zurückgelegte Strecke in einer Zeit ($\Delta s$) gleich die Position ($s$) und die Ausgangsstellung ($s_0$):
| $ \Delta s = s - s_0 $ |
und der Abgelaufene Zeit ($\Delta t$) ist gleich der Zeit ($t$) und der Startzeit ($t_0$):
| $ \Delta t \equiv t - t_0 $ |
Die Gleichung f r die durchschnittliche Geschwindigkeit:
| $ v_0 \equiv\displaystyle\frac{ \Delta s }{ \Delta t }$ |
kann geschrieben werden als:
$v_0 = \bar{v} = \displaystyle\frac{\Delta s}{\Delta t} = \displaystyle\frac{s - s_0}{t - t_0}$
somit ergibt sich, wenn man nach ihr aufl st:
| $ s = s_0 + v_0 ( t - t_0 )$ |
(ID 3154)
Wenn man von die Ausgangsstellung ($s_0$) ausgeht und die Zurückgelegte Strecke in einer Zeit ($\Delta s$) berechnen möchte, muss ein Wert für die Position ($s$) festgelegt werden.
In einem eindimensionalen System erhält man die Zurückgelegte Strecke in einer Zeit ($\Delta s$), indem man die Ausgangsstellung ($s_0$) von die Position ($s$) subtrahiert. Das ergibt:
| $ \Delta s = s - s_0 $ |
(ID 4352)
Wenn man von die Ausgangsstellung ($s_0$) ausgeht und die Zurückgelegte Strecke in einer Zeit ($\Delta s$) berechnen möchte, muss ein Wert für die Position ($s$) festgelegt werden.
In einem eindimensionalen System erhält man die Zurückgelegte Strecke in einer Zeit ($\Delta s$), indem man die Ausgangsstellung ($s_0$) von die Position ($s$) subtrahiert. Das ergibt:
| $ \Delta s = s - s_0 $ |
(ID 4352)
Beispiele
Das Modell konstanter Geschwindigkeit beschreibt eine Bewegung w hrend eines Abschnitts oder Zeitintervalls, in dem die Geschwindigkeit des Objekts als konstant angesehen werden kann. Eine komplexere Bewegung kann jedoch mehrere Abschnitte oder Intervalle umfassen, in denen sich die Geschwindigkeit ndert und sogar umkehren kann (negativ wird), was darauf hinweist, dass sich das Objekt zur ckbewegt.
Wenn zwei Modelle konstanter Geschwindigkeit als aufeinanderfolgende Bewegungen kombiniert werden, kann man sie verbinden, indem man die Endpositionen und -zeiten der ersten Phase mit den Anfangspositionen und -zeiten der zweiten gleichsetzt. So ergeben sich die Distanzen die In der ersten Etappe zurückgelegte Strecke ($\Delta s_1$) und die In der zweiten Etappe zurückgelegte Strecke ($\Delta s_2$), die mit den Geschwindigkeiten die Geschwindigkeit der ersten Stufe ($v_1$) und die Geschwindigkeit der zweiten Stufe ($v_2$) zur ckgelegt werden. Diese Werte k nnen ver ndert werden, einschlie lich der Umkehr der Bewegung durch Zuweisung negativer Geschwindigkeiten und Starten der Simulation mit der Schaltfl che 'start'.
(ID 15383)
Im Fall einer Bewegung in zwei Stufen bewegt sich zuerst das Objekt eine Entfernung von eine In der ersten Etappe zurückgelegte Strecke ($\Delta s_1$) w hrend einer Zeit von ein In der ersten Phase verstrichene Zeit ($\Delta t_1$) mit einer Geschwindigkeit von eine Geschwindigkeit der ersten Stufe ($v_1$).
| $ v_1 \equiv\displaystyle\frac{ \Delta s_1 }{ \Delta t_1 }$ |
Dann, in einer zweiten Stufe, bewegt es sich eine Entfernung von eine In der zweiten Etappe zurückgelegte Strecke ($\Delta s_2$) w hrend einer Zeit von ein In der zweiten Phase verbrachte Zeit ($\Delta t_2$) mit einer Geschwindigkeit von eine Geschwindigkeit der zweiten Stufe ($v_2$).
| $ v_2 \equiv\displaystyle\frac{ \Delta s_2 }{ \Delta t_2 }$ |
Wenn dies grafisch dargestellt wird, erhalten wir ein Positions-Zeit-Diagramm wie folgt:
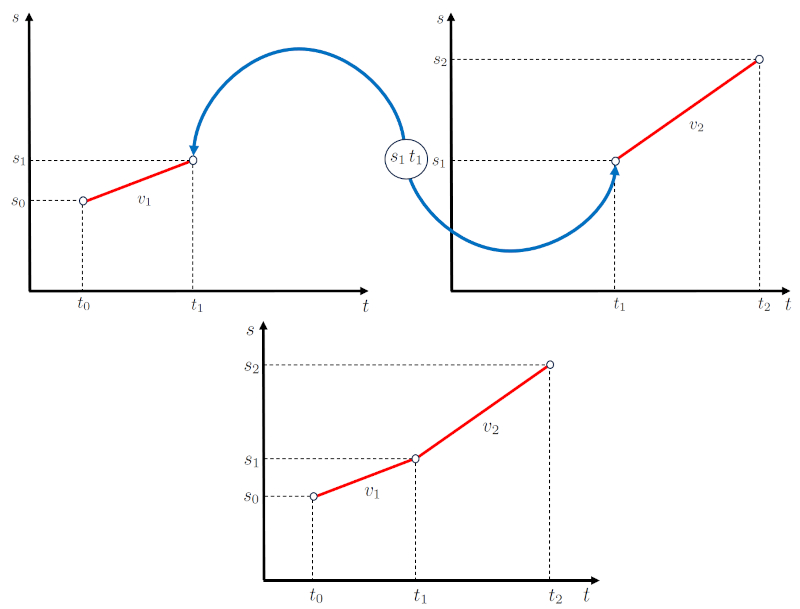
Der Schl sselpunkt ist, dass der In der ersten Phase verstrichene Zeit ($\Delta t_1$) und der In der zweiten Phase verbrachte Zeit ($\Delta t_2$) sequenziell sind, genauso wie die In der ersten Etappe zurückgelegte Strecke ($\Delta s_1$) und die In der zweiten Etappe zurückgelegte Strecke ($\Delta s_2$).
(ID 15504)
Im Fall einer Bewegung in zwei Stufen bewegt sich zuerst das Objekt eine Entfernung von eine In der ersten Etappe zurückgelegte Strecke ($\Delta s_1$) w hrend einer Zeit von ein In der ersten Phase verstrichene Zeit ($\Delta t_1$) mit einer Geschwindigkeit von eine Geschwindigkeit der ersten Stufe ($v_1$).
| $ v_1 \equiv\displaystyle\frac{ \Delta s_1 }{ \Delta t_1 }$ |
Dann, in einer zweiten Stufe, bewegt es sich eine Entfernung von eine In der zweiten Etappe zurückgelegte Strecke ($\Delta s_2$) w hrend einer Zeit von ein In der zweiten Phase verbrachte Zeit ($\Delta t_2$) mit einer Geschwindigkeit von eine Geschwindigkeit der zweiten Stufe ($v_2$).
| $ v_2 \equiv\displaystyle\frac{ \Delta s_2 }{ \Delta t_2 }$ |
Wenn dies grafisch dargestellt wird, erhalten wir ein Positions-Zeit-Diagramm wie folgt:
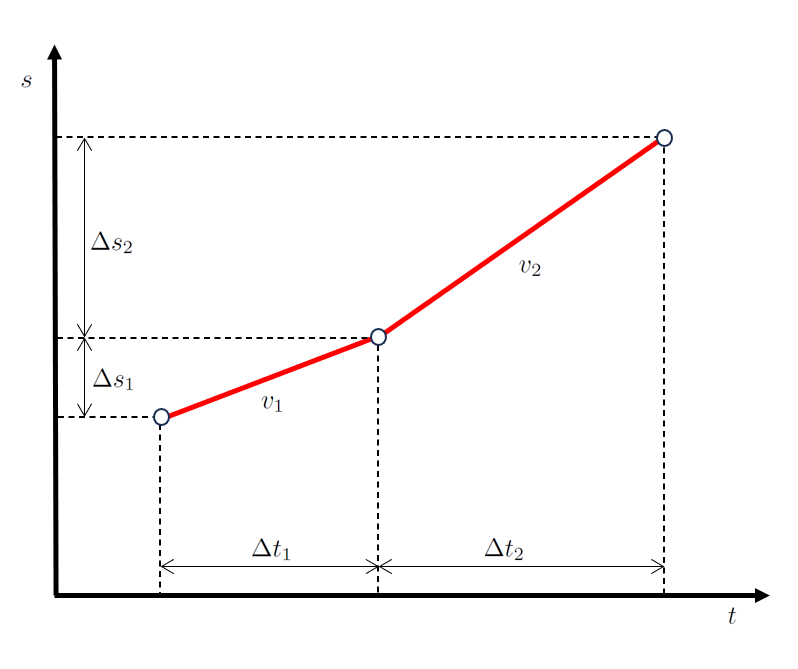
Der Schl sselpunkt ist, dass der In der ersten Phase verstrichene Zeit ($\Delta t_1$) und der In der zweiten Phase verbrachte Zeit ($\Delta t_2$) sequenziell sind, genauso wie die In der ersten Etappe zurückgelegte Strecke ($\Delta s_1$) und die In der zweiten Etappe zurückgelegte Strecke ($\Delta s_2$).
(ID 15395)
Im Falle einer Bewegung in zwei Etappen kann die erste Etappe durch eine Funktion beschrieben werden, die die Punkte der Startzeit ($t_0$), der Endzeit der ersten und Beginn der zweiten Etappe ($t_1$), die Ausgangsstellung ($s_0$) und der Erste Endposition und begonnene zweite Etappe ($s_1$) einbezieht und durch eine Gerade mit einer Steigung von die Geschwindigkeit der ersten Stufe ($v_1$) dargestellt wird:
| $ s_1 = s_0 + v_1 ( t_1 - t_0 )$ |
F r die zweite Etappe, definiert durch die Punkte der Erste Endposition und begonnene zweite Etappe ($s_1$), die Endposition der zweiten Etappe ($s_2$), der Endzeit der ersten und Beginn der zweiten Etappe ($t_1$) und der Endzeit der zweiten Etappe ($t_2$), wird eine zweite Gerade mit einer Steigung von die Geschwindigkeit der zweiten Stufe ($v_2$) verwendet:
| $ s_2 = s_1 + v_2 ( t_2 - t_1 )$ |
die wie folgt dargestellt wird:
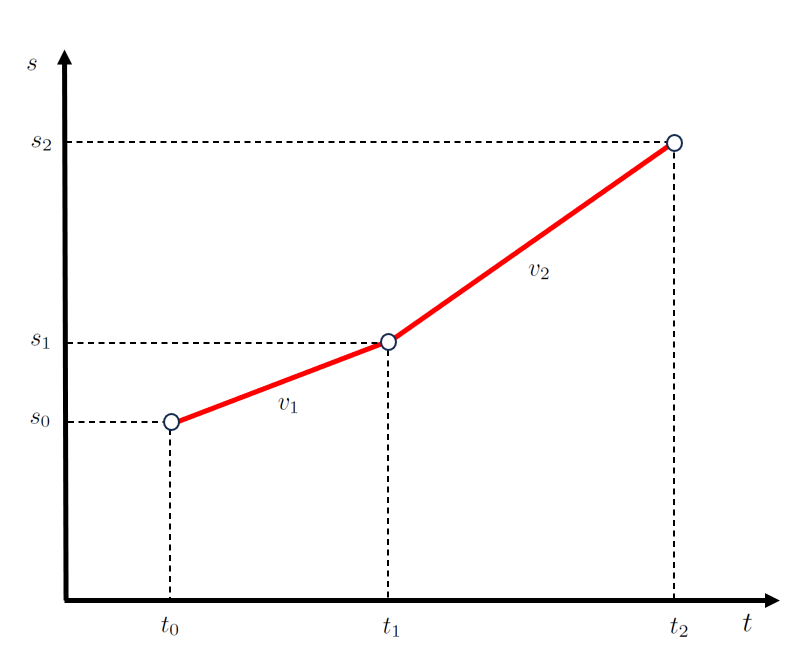
Es ist wichtig zu beachten, dass der Beginn der zweiten Etappe, definiert durch die Punkte der Endzeit der ersten und Beginn der zweiten Etappe ($t_1$) und der Erste Endposition und begonnene zweite Etappe ($s_1$), mit dem Ende der ersten Etappe zusammenf llt.
(ID 15396)
Das Basismodell beinhaltet zwei Bewegungen in aufeinanderfolgenden Etappen.
In der ersten Etappe beginnt man bei die Ausgangsstellung ($s_0$) und endet bei der Erste Endposition und begonnene zweite Etappe ($s_1$), wobei eine Strecke von die In der ersten Etappe zurückgelegte Strecke ($\Delta s_1$) zur ckgelegt wird, die bei der Startzeit ($t_0$) beginnt und bei der Endzeit der ersten und Beginn der zweiten Etappe ($t_1$) endet, mit einer Dauer von der In der ersten Phase verstrichene Zeit ($\Delta t_1$) und einer Geschwindigkeit von die Geschwindigkeit der ersten Stufe ($v_1$).
In der zweiten Etappe beginnt man bei der Erste Endposition und begonnene zweite Etappe ($s_1$) und endet bei die Endposition der zweiten Etappe ($s_2$), wobei eine Strecke von die In der zweiten Etappe zurückgelegte Strecke ($\Delta s_2$) zur ckgelegt wird, die bei der Endzeit der ersten und Beginn der zweiten Etappe ($t_1$) beginnt und bei der Endzeit der zweiten Etappe ($t_2$) endet, mit einer Dauer von die In der zweiten Etappe zurückgelegte Strecke ($\Delta s_2$) und einer Geschwindigkeit von die Geschwindigkeit der zweiten Stufe ($v_2$).
Das resultierende Diagramm besteht aus zwei Teildiagrammen, in denen eine konstante Geschwindigkeit herrscht. Beide Diagramme sind durch der Erste Endposition und begonnene zweite Etappe ($s_1$) und der Endzeit der ersten und Beginn der zweiten Etappe ($t_1$) verbunden, die dem Endpunkt der ersten Etappe und dem Anfangspunkt der zweiten Etappe entsprechen.

Damit ergibt sich folgende Netzwerkstruktur des Modells:
(ID 15384)
ID:(1448, 0)
