Resistor connected in series with a parallel LC system
Image 
Si se conecta una resistencia en serie con una inductancia y capacitancia que están conectadas en paralelo se tiene el siguiente diagrama:

ID:(12288, 0)
Resistance of a resistor connected in series with an LC system
Equation 
La resistencia de sistema de resistencia en serie con un sistema de inductancia y capacitancia en paralelo depende de la resistencia individual y del sistema LC.
En particular con es
| Z_s ^2 = R ^2 + X ^2 |
ID:(12290, 0)
Potential differences in series sum of R with parallel LC
Equation 
La diferencia de potencial total es con
| \Delta\varphi_{Rs} ^2= \Delta\varphi_R ^2 + \Delta\varphi_X ^2 |
ID:(12292, 0)
Parallel potential and current relationship of R and LC circuit
Equation 
La relación entre potencial y corriente para la suma en serie de una sistema de una resistencia con un sistema LC
ID:(12294, 0)
Parallel Connected Resistor with a Parallel LC System
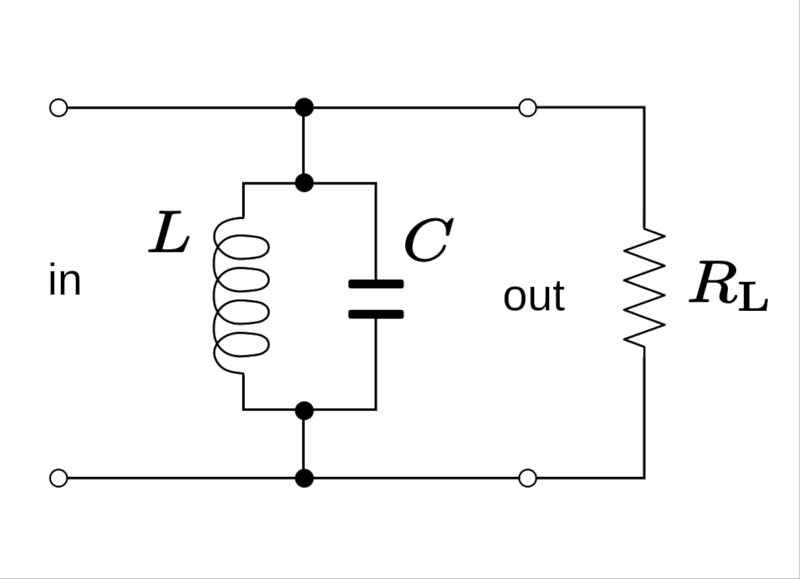
Image 
Si se conecta una resistencia en paralelo con una inductancia y capacitancia que están conectadas en paralelo se tiene el siguiente diagrama:
ID:(12289, 0)
Resistance of a resistor connected in parallel with an LC system
Equation 
La resistencia de sistema de resistencia en paralelo con un sistema de inductancia y capacitancia en paralelo depende de la resistencia individual y del sistema LC.
En particular con es
| \displaystyle\frac{1}{ Z_p ^2} =\displaystyle\frac{1}{ R ^2 }+\displaystyle\frac{1}{ X ^2} |
ID:(12291, 0)
Current in parallel sum of resistance with LC in parallel
Equation 
La corriente es con
| I_{Rp} ^2 = I_R ^2 + I_X ^2 |
ID:(12293, 0)
Series potential and current relationship of R and LC circuit
Equation 
La relación entre potencial y corriente para la suma en paralelo de una resistencia con un sistema LC en paralelo es con
| \Delta\varphi_{Rs} = Z_s I_{Rs} |
ID:(12295, 0)
Current phase difference electrical potential difference
Equation 
Los sistemas R-LC generan una diferencia de fase entre la corriente y el potencial eléctrico.
Este se puede calcular con mediante
| \tan\phi = \displaystyle\frac{1}{ R }\left( L \omega -\displaystyle\frac{1}{ C \omega } \right) |
ID:(12296, 0)
LC Resonance
Equation 
La suma de la resistencia en inductancia y capacitancia pueden oscilar de modo de que con
| X_s = \omega L - \displaystyle\frac{1}{ \omega C } |
puede ser singular si con es
| \omega ^2 = \displaystyle\frac{1}{ L C } |
que corresponde a una resonancia.
ID:(12287, 0)
